Файл: Проектирование редуктора вертолёта.docx

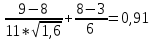
KFa= Так как неравенство выполняется, принимаем КFа =0,91ΚFβ- коэффициент, учитывающий неравномерность распределения нагрузки по длине зубаΚFβ= ΚΗβ= 1,09 ( по п.2.8.2 ), т.к. значения коэффициента одинаковы при расчёте на зубья 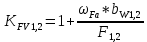(4.1.5)гдеbW_1,2 - рабочая ширина венца шестерни и колеса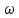FV- удельная окружная динамическая нагрузка на зубья, определяемая изнеравенства: 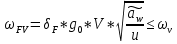(4.1.6)гдеδ_F- коэффициент, учитывающий модификацию головки зуба и твердость рабочих поверхностей, выбирается из таблицы 1.9 [1]δΗ= 0,010 - для прямых зубьев с модификацией головок по п.5.1.3 [1]g0- коэффициент, учитывающий погрешность зацепления по шагу, выбирается изтаблицы 1.16 [1]g₀ = 61 - для 8 степени точности при m = 2,5мм< 3,55 мм;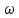V

---

—предельное значение удельной окружной динамической силы , выбираетсяиз таблицы 1.16 [1]

ων= 410 Н/ мм - для 8 степени точности при m= 8мм> 3,55 мм
После подстановки числовых значений в формулу (4.1.6)



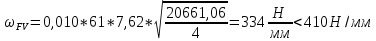
Так как неравенство выполняется, окончательное значение удельной окружной динамической нагрузки на зубья ωFν= 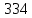Н / мм

Тогда коэффициент, учитывающий дополнительную динамическую нагрузку на зубья:





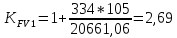
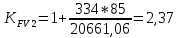
В результате после подстановки удельная расчётная окружная нагрузка на зубья шестерни и колеса при расчёте на изгиб:

_F1 =

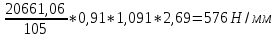
_F2 =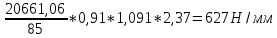

4.1.4 Расчётные местные напряжения изгиба у основания зубьев шестерни и колеса

σ_F1 = Υ_F1* Υβ*

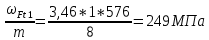
σ_F2 = Υ_F

---

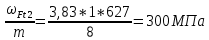
2* Υβ* 4
(4.2.1)
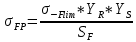
.2 Определение допускаемых напряжений изгиба в расчётных точках зубьев шестерни и колеса, работающих в условиях частого реверсирования 4.2.1 Определение предельных напряжений изгиба при двухстороннем приложении нагрузки в зубьях шестерни и колесаПредельные напряжения изгиба σ_Flim при одностороннем приложении нагрузки зависят от числа циклов напряжений и для стальных зубьев определяются из неравенства:
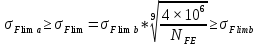
(4.2.2)
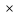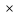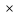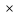Для стальных зубьев при НВ> 350 верхний и нижний пределы выбираются согласно рекомендациям табл. 1.17:Для шестерниσ_Flima= 1600 МПаσ_Flimb= 950 МПаДля колесаσ_Flima= 20НRС+500 = 20 53+500=1560МПаσ_Flimb=12НRС+300 = 12 53+300=936МПаРасчётное число циклов изменения напряжений изгиба:N_FE=60 c n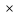 N_ЦН (4.2.3)Число зацеплений за один оборот с =1По исходным данным число циклов нагружения передачи NЦН=

---

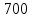
циклов.

Частота вращения шестерни n₁ = об / мин

Частота вращения колеса n2 = 330об / мин

После подстановки числовых значений в формулу (4.2.3)

N_FE1=t_FE c n₁ N_ЦН=60 1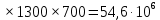

N_FE2=t_FE c n₂ N_ЦН=60 1 330 =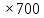




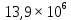
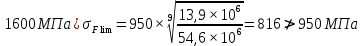
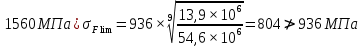
Так как неравенства не выполняются принимаем:

σ_Flim1 = 950 МПа

σ_Flim2 = 936 МПа

Предельные напряжения изгиба для двухстороннего приложения нагрузки:

σ
(4.2.4)
-_{F lim} = σ_{F lim} (1-γ_FC δ_F δ_N)

где согласно рекомендациям п.5.2.1 [1]:

γ_FC =0,25 - коэффициент, определяющий относительное снижение предела выносливостиприR= -1 при НВ >

---

450

δΡ- коэффициент, учитывающий несимметричность знакопеременной циклограммы нагружения; при одинаковой величине нагрузки по положительной и отрицательной сторонам циклограммы δF =1

δN- коэффициент, учитывающий соотношение эквивалентных чисел циклов изменения изгибного напряжения по положительной и отрицательной сторонам циклограммы; при одинаковом времени работы по обеим сторонам циклограммы δΝ= 1

После подстановки числовых значений

σ-_Flim1= 950 (1-0,25 1 1)=712,5 МПа

σ-_Flim2= 936 ( 1-0,25 1 1)=702 МПа

4.2.2 Коэффициент, учитывающий влияние шероховатости переходной поверхности у основания зуба на изгибную прочность

Y_R1=Y_R2=1,05 – при шлифованных поверхностях НВ>350

4.2.3 Коэффициент, учитывающий чувствительность материала зубьев к концентрации напряжений и масштабный эффект

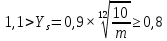(4.2.5)

После подстановки числовых значений



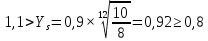
Так как неравенства выполняются, принимаем: Y_s=0,92

4.2.4 Коэффициент безопасности при расчёте зубьев на изгиб

Величина S_F зависит от требуемой вероятности безотказной работы. Вероятность безотказной работы зубчатой пары Р>0,

S_F=2,2 -в соответствии с назначением механизма и рекомендациями п.5.2.4

---