Файл: Шыармашылы топ авторрастырушылар.docx

4. 
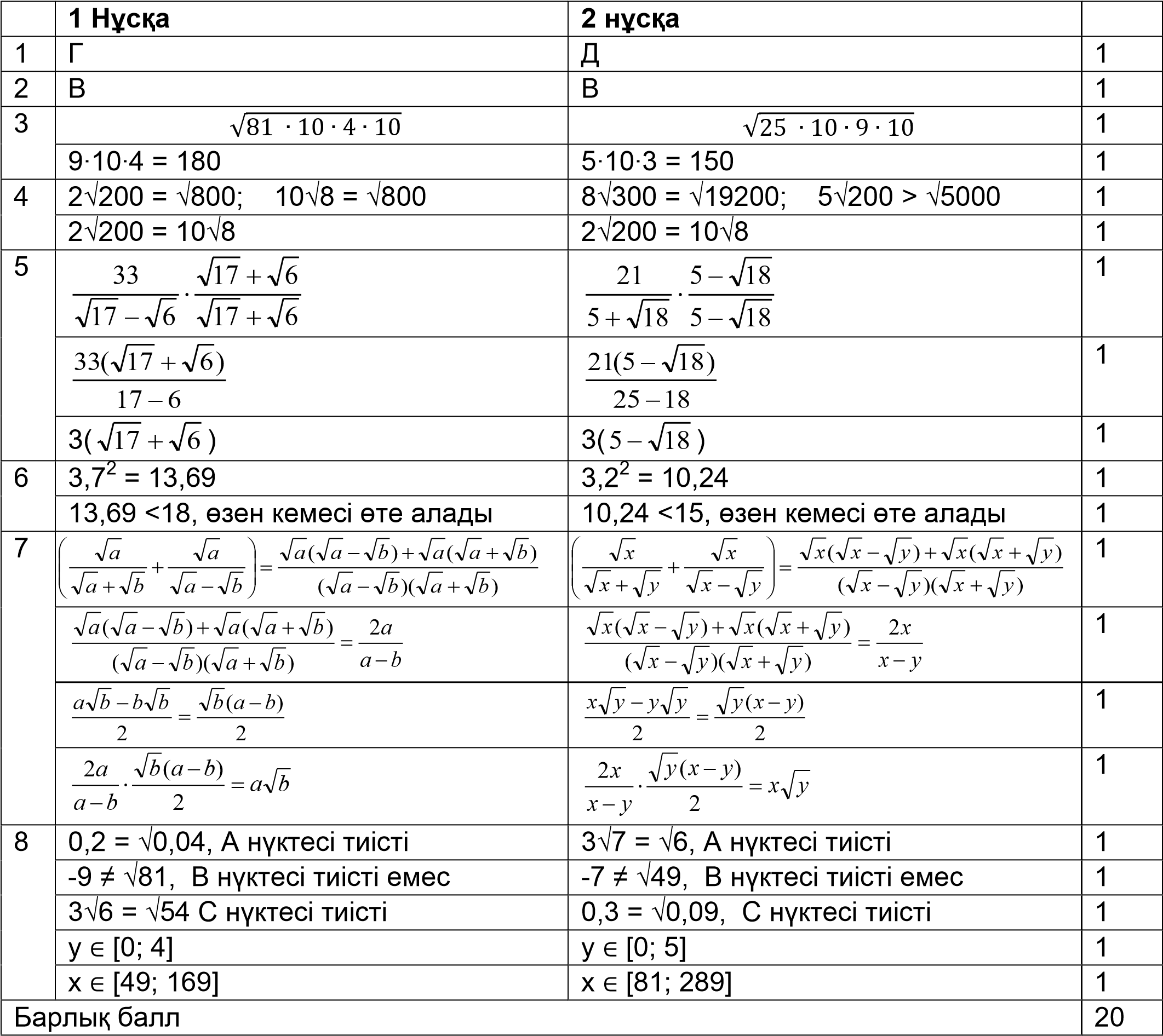
   [2 балл] Сандарды салыстырыңыз: 2 200 және 10 8
   

5. 
   [3 балл] бӛлшек бӛлімін иррационалдықтан арылтыңыз :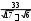
   

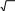
6. 
   [2 балл] Ӛзендегі кӛпірдің биіктігі 18 м. Осы кӛпірдің астынан биіктігі су деңгейінен 3,7 м болатын ӛзен кемесі ӛте ала ма?
   

2 нұсқа

1. 
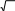
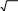
   [1 балл] 11; 25 ; 0; -2,6767… ; 29 ; 6,3; 78; 1,(3);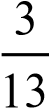 ; π; 5 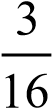нақты сандарының ішінен иррационал сандарды таңдаңыз.
   

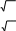
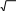А) 1,(3) және 25 Б) π және -2,6767 В) 25 және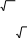

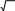Г) 25 және 29 Д) 29 және π

2. 
   [1 балл] 5 саны тӛмендегі сан аралықтарының қайсысына тиісті:
   

А) (0; 1,5) Б) (-0,5; 0,5) В) (2,1; 2,5) Г) (1,5; 2,1) Д) (20; 25)

3. 
   [1 балл] Есептеңіз: 25090
   

4. 
   [2 балл] Сандарды салыстырыңыз: 8 300 и 5 200
   

5. 
   [3 балл] бӛлшек бӛлімін иррационалдықтан арылтыңыз :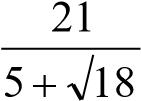
   

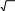
6. 
   [2 балл] Ӛзендегі кӛпірдің биіктігі 15 м. Осы кӛпірдің астынан биіктігі су деңгейінен 3,2 м болатын ӛзен кемесі ӛте ала ма?
   

Бағалау кестесі

---

ІІ тоқсанға арналған ТЖБ

Бөлім Кадраттық теңдеу

Оқу мақсаттары

8.2.2.1 квадрат теңдеудің анықтамасын білу

8.2.2.3 квадрат теңдеулерді шешу

8.2.2.4 Виет теоремасын қолдану

8.2.1.3 квадрат ҥшмҥшені кӛбейткіштерге жіктеу

8.2.2.2 кваеңдеудің тҥрлерін ажырата білу

8.2.2.5 |ax²+bx|+c=0; ax²+b|x|+c=0 тҥріндегі теңдеулерді шешу

8.2.2.6 бӛлшек-рационал теңдеулерді шешу

Ойлау дағдыларының деңгейі: Білу және тҥсіну. Қолдану

Орындау уақыты 40 минут

І нҧсқа

1. [2 балл] (х + 3)² + 7х = 4х(х – 9) теңдеуін ах² + bх + с = 0 тҥріне келтіріңдер және бірінші, екінші, бос мҥшені кӛрсетіңіз

2.

а) [1 балл] Тӛмендегі теңдеулердің қайсысы келтірілген квадрат теңдеулер:

А) – х² + 6х – 1 = 0

Б) х + 2х² – 5 = 0 2

В) – 3х + 1 = 0

2

Г) 7х + х² – 3 = 0

Д) 3х² – 6х + 12 = 0

б) [1 балл] Берілген тҥбірлер бойынша келтірілген кадрат теңдеуді қҧрастырыңыз:

х₁= 3, х₂ = – 1. A) x² + 3х – 2 = 0

Б) – x² + 2х – 3 = 0

В) x² – 2х – 3 = 0

Г) – x² – 2х + 3 = 0

Д) x² + 3х +2 = 0

3. 
   [3 балл] 3х² – 6х + с = 0 квадрат теңдеуі берілген.
   

а) с параметрінің қандай мәнінде теңдеудің ӛзара тең екі тҥбірі бар.

б) теңдеудің осы тҥбірлерін табыңыз

3. 
   [2 балл] х² – 16х + 63 = 0 теңдеуінің тҥбірлерін таппай тӛмендегілерді табыңыз: а) х₁ + х₂; х₁ ∙ х₂
   

1 1

б) 

12

3. 
   [3 балл] х² – 6х + 8 квадрат ҥшмҥшелігі ҥшін:
   

а)толық квадратты айрыңыз;

б) квадрат ҥшмҥшені кӛбейткіштерге жіктеңіз

2 8

3. 
   [4 балл] берілген теңдеу бойынша 33₂ 9 _
   

а) теңдеудің мҥмкін мәндер облысын анықтаңыз;

б) рационал теңдеуді квадраттық теңдеу тҥріне келтіріңіз

в) рационал теңдеуді шешіңіз

3. 
   [4 балл] Теңдеуді шешіңіз: х² – 7|х| + 12 = 0
   

ІІ нҧсқа

1. [2 балл] (х + 2)² + 5х = 3х(х – 8) теңдеуін ах² + bх + с = 0 тҥріне келтіріңдер және бірінші, екінші, бос мҥшені кӛрсетіңіз

---

2.

а) [1 балл] Берілген тҥбірлер бойынша келтірілген кадрат теңдеуді қҧрастырыңыз:

А) х + 3х² – 7 = 0

2

Б) – 4х + 9 = 0

3

В) – х² + 5х – 2 = 0

Г) 4х² – 8х + 12 = 0

Д) 9х + х² – 2 = 0

б) [1 балл] Берілген тҥбірлер бойынша келтірілген кадрат теңдеуді қҧрастырыңыз: х₁=5, х₂ = –2. A) x² – 3х +10 = 0

Б) – x² + 2х – 7 = 0

В) x² – 3х – 10 = 0

Г) – x² – 3х + 10 = 0

Д) x² – 3х +7 = 0

3. 
   [3 балл 4х² – 8х + с = 0 квадрат теңдеуі берілген.
   

а) с параметрінің қандай мәнінде теңдеудің ӛзара тең екі тҥбірі бар.

б) теңдеудің осы тҥбірлерін табыңыз

3. 
   [2 балл] х² – 17х + 72 = 0 теңдеуінің тҥбірлерін таппай тӛмендегілерді табыңыз:
   

а) + ;

1 1

б) 

12

3. 
   [3 балл] х² – 6х + 5 квадрат ҥшмҥшелігі ҥшін:
   

а)толық квадратты айрыңыз;

б) квадрат ҥшмҥшені кӛбейткіштерге жіктеңіз

5 8

3. 
   [4 балл] берілген теңдеу бойынша 22₂ 4
   

а) теңдеудің мҥмкін мәндер облысын анықтаңыз;

б) рационал теңдеуді квадраттық теңдеу тҥріне келтіріңіз

в) рационал теңдеуді шешіңіз

3. 
   [4 балл] Теңдеуді шешңіңз: х² – 8|х| + 12 = 0
   

Бағалау кестесі

	І нҧсқа	ІІ нҧсқа
1	– 3х2 + 49х + 9 = 0 немесе 3х2 – 49х – 9 = 0	– 2х2 + 33х + 4 = 0 немесе 2х2 – 33х – 4 = 0	1
	а = – 3 b = 49 c = 9 немесе а = 3 b = – 49 c = – 9	а = – 2 b = 33 c = 4 немесе а = 2 b = – 33 c = – 4	1
2 а	Г	Д	1
2 б	В	В	1
3	D = 36 – 12с = 0	D = 64 – 16с = 0	1
	с = 3	с = 4	1
	х1 = х2 = 1	х1 = х2 = 1	1
4	х1 + х2 = 16; х1 ∙ х2 = 63	х1 + х2 = 17; х1 ∙ х2 = 72	1
	1 12 1 16    12 1 2 63	1 12 1 17    12 1 2 72	1
5	х2 – 6х + 8 = (х – 3)2 – 1	х2 – 6х + 5 = (х – 3)2 – 4	1
	х2 – 6х + 8 = 0 х1 = 2, х2 = 4	х2 – 6х + 5 = 0 х1 = 1, х2 = 5	1
	х2 – 6х + 8 = (х – 2) (х – 4)	х2 – 6х + 5 = (х – 1) (х – 5)	1
6	ОДЗ : х ≠ −3; х ≠ 3	ОДЗ : х ≠ −2; х ≠ 2	1
	Бӛлшекті ортақ бӛлімге келтіреді, алымын 0-ге теңестіреді	Бӛлшекті ортақ бӛлімге келтіреді, алымын 0-ге теңестіреді	1
	Квадрат теңдеуді шешеді x2 + х – 2 = 0	Квадрат теңдеуді шешеді x2 – х – 2 = 0	1
	Теңдеудің тҥбірлерін табады х1 = − 2, х2 = 1	Теңдеудің тҥбірлерін табады х1 = − 1, х2 = 2	1
7	х2 – 7|х| + 12 = 0, t = |х| t2 – 7t + 12 = 0	х2 – 8|х| + 12 = 0, t = |х| t2 – 8t + 12 = 0	1
	t1 = 3 t2 = 4	t1 = 2 t2 = 6	1
	|х| = 3 x1;2 = ± 3	|х| = 2 x1;2 = ± 2	1
	|х| = 4 x3;4 = ± 4 Жауабы: {-4; -3; 3; 4}	|х| = 6 x3;4 = ± 6 Жауабы: {-6; -2; 2; 6}	1
	Барлық балл		20

---

---

ІІІ тоқсанға арналған ТЖБ

Бөлім

Кадрат теңдеулер

Квадраттық функция Статистика элементтері

Оқу мақсаттары

8.4.2.1 мәтінді есептерді квадрат теңдеулердің кӛмегімен шешу

8.4.2.2 мәтінді есептерді бӛлшек-рационал теңдеулердің кӛмегімен шешу

8.4.1.2 = ( − )² , = х²+ және = ( − )²+ , ≠0, тҥрдегі квадраттық



8.4.1.4 аргументтің берілген мәндері бойынша функцияның мәндерін табу және функцияның мәні бойынша аргументтің мәнін табу

8.4.2.3 қолданбалы есептерді шығару ҥшін квадраттық функцияны қолдану

8.3.3.2 жиіліктердің интервалдық кестесінің деректерін жиіліктер гистограммасы арқылы беру 8.3.3.3 жинақталған жиілік анықтамасын білу

8.3.3.5 дисперсия, стандартты ауытқу анықтамаларын және оларды есептеу формулаларын білу

Ойлау дағдыларының деңгейі: Білу және тҥсіну. Қолдану

Орындау уақыты 40 минут

І нҧсқа

1. 
   [1 балл] кестеде аяқ киім ӛлшемдерінің сатылу жиілігі кӛрсетілген. Жинақталған жиілікті таюыңыз.
   

39	40	41	42	43
2	3	5	6	4

---