Файл: Методические материалы по курсу экономикоматематическое моделирование.doc
Добавлен: 05.12.2023
Просмотров: 125
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Варианты заданий по теме 3
Вариант 1
Составить двойственную задачу к исходной ЗЛП.
Z = -2x1 + x2 → min
x1 - x2 ≤ 3
x1 + x2 ≤ 9
-x1 + x2 ≥ 3
x1 + x2 ≥ 3/2
x1 ≥0, x2 ≥0
Вариант 2
Составить двойственную задачу к исходной ЗЛП.
Z = 4x1 + 3x2 → max
-x1 + 3x2 ≤ 9
2x1 + 3x2 ≤ 18
2x1 - x2 ≤ 10
x1 ≥0, x2 ≥0
Вариант 3
Составить двойственную задачу к исходной ЗЛП.
Z = x1 + x2 → max
-x1 + x2 ≤ 1
x1 + 2x2 ≤ 10
x1 + 2x2 ≥ 2
2x1 + x2 ≤ 10
x1 ≥0, x2 ≥0
Вариант 4
Составить двойственную задачу к исходной ЗЛП.
Z = 2x1 + x2 → max
x1 + x2 ≤ 8
3x1 - 2x2 ≤ 12
-x1 + 2x2 ≤ 8
2x1 + 3x2 ≥ 6
x1 ≥0, x2 ≥0
Вариант 5
Составить двойственную задачу к исходной ЗЛП.
Z = x1 - 3x2 → max
x1 - x2 ≤ 3
2x1 + x2 ≥ 3
x1 - 3x2 ≤ 1
x1 ≥0, x2 ≥0
Вариант 6
Составить двойственную задачу к исходной ЗЛП.
Z = 3x1 + 5x2 → min
x1 + x2 ≤ 5
3x1 - x2 ≤ 3
x1 ≥0, x2 ≥0
Вариант 7
Составить двойственную задачу к исходной ЗЛП.
Z = -2x1 + x2 → min
x1 - x2 ≤ 3
x1 + x2 ≤ 9
-x1 + x2 ≥ 3
x1 + x2 ≥ 3/2
x1 ≥0, x2 ≥0
Вариант 8
Составить двойственную задачу к исходной ЗЛП.
Z = 2x1 + 2x2 → min
x1 + 3x2 ≥ 3
-2x1 + x2 ≤ 2
x1 + x2 ≤ 5
x1 ≥0, x2 ≥0
Вариант 9
Составить двойственную задачу к исходной ЗЛП.
Z = 2x1 + 2x2 → max
x1 + 3x2 ≥ 3
-2x1 + x2 ≤ 2
x1 + x2 ≤ 5
x1 ≥0, x2 ≥0
Вариант 10
Составить двойственную задачу к исходной ЗЛП.
Z = 2x1 + 3x2 → min
x1 + x2 ≤ 4
6x1 + 2x2 ≥ 6
x1 + 5x2 ≥ 5
x1 ≥0, x2 ≥0
Тема 4. Транспортная задача
Пример задачи.
Мощности поставщиков: А1 = 120 т; А2 = 220 т; А3 = 300 т; А4 = 170 т. Спрос потребителей: В1 = 120 т; В2 = 250 т; В3 = 200 т; В4 = 180 т. Удельные затраты на перевозку единицы груза представлены матрицей С:
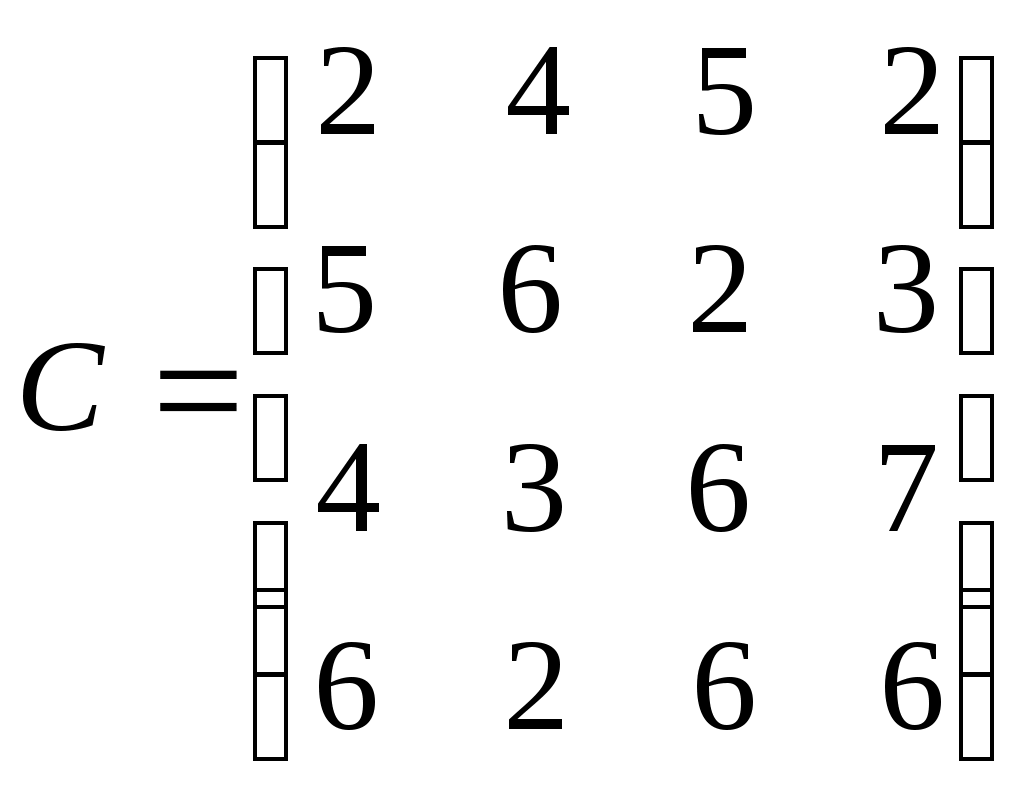
Определить объемы перевозок из пункта i в пункт j такие, чтобы суммарные издержки на перевозку были бы минимальными, т.е. построить матрицу объемов перевозок х.
Решение задачи:
1. Определить тип задачи – закрытый или открытый.
Задача открытая, т.к.
Вводится фиктивный потребитель с объемом потребления Вф
2. Строится расчетная матрица с фиктивным потреблением Вф и удельными затратами на перевозку фиктивного груза Ciф = 0. Исходное опорное решение поставленной транспортной задачи см. табл. 12.
Таблица 12
-
120
250
200
180
Вф
120
2
120
4
5
2
0
0
220
5
6
2
200
3
20
0
300
4
3
80
5
7
160
0
60
170
6
2
170
6
6
0
3. Формируется опорный план перевозок по критерию наименьших удельных затрат на перевозку единицы груза, т.е. minCij. Затраты Cij = 0 на перевозку фиктивных грузов не принимаются во внимание. Оставшиеся мощности сносятся фиктивному потребителю
Проверяется баланс по строкам и столбцам.
4. Проверяется полученный план перевозок на вырожденность:
K = m + n – 1 - план невырожденный,
K < m + n – 1 - план вырожденный,
где K - количество занятых клеток в таблице 12, т.е. количество
m - количество строк матрицы;
n - количество столбцов.
В нашем примере задача вырожденная (7 < 4 + 5 – 1). Число занятых клеток К меньше значения (m + n – 1) на 1. Поэтому одну клетку нужно дополнительно заполнить нулевой поставкой. Такие клетки называют условно-занятыми. Нуль помещают в такую клетку, чтобы в каждой строке и столбце было не менее одной занятой клетки. Поместим нулевую поставку в клетку (1,4), т.е. х14 = 0. Теперь задача стала невырожденной.
5. Оптимизируем опорный план, используя метод потенциалов.
Определяем потенциалы строк Ui и столбцов Vj по формуле:
Для этого зададим одно любое значение потенциала Ui либоVj, например, U3 = 0.
Пересчитаем все остальные Ui , Vj по (1) и зафиксируем их в таблице 12:
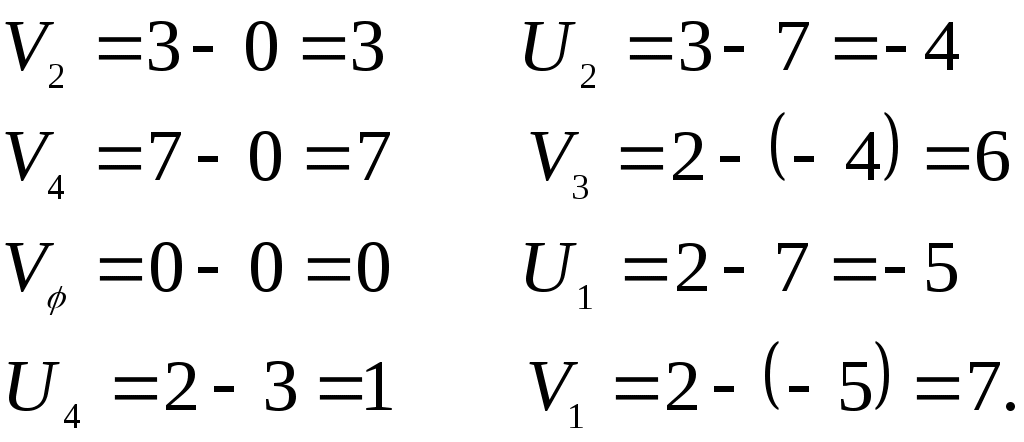
6. Определяются оценки свободных клеток:
Eij = Cij – (Ui + Vj) 0 (2)
Е12 = 4 – (- 5 + 3) = 6 Е31 = 4 – (0 + 7) = - 3
Е13 = 5 – (- 5 + 6) = 4 Е33 = 6 – (0 + 6) = 0
Е1ф = 0 – (- 5 + 0) = 5 Е41 = 6 – (- 1 + 7) = 0
Е21 = 5 – (- 4 + 7) = 2 Е43 = 6 – (- 1 + 6) = 1
Е22 = 6 – (- 4 + 3) = 7 Е44 = 6 – (- 1 + 7) = 0
Е2ф = 0 – (- 4 + 0) = 4 Е4ф = 0 – (- 1 + 0) = 1.
7. Условие оптимальности задачи: Е ij
В нашем примере имеется отрицательная оценка (Е31 = – 6). Для клетки (3,1) строим цикл (цепь, многоугольник) для перераспределения поставок. Все его вершины, кроме одной, должны находиться в занятых клетках, углы прямые, число вершин четное. Для указанной клетки (3,1) построим цикл отдельно (рис. 2а). Около свободной клетки цикла ставится знак (+), далее поочередно проставляются знаки (-) и (+). У вершин со знаком (-) выбирается минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+) и отнимают от грузов у вершин со знаком (-). В результате перераспределения груза получим новые значения грузов в вершинах цикла (рис. 2б).





 – +
– + 


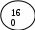
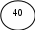

120

 + –
+ –Рис. 2а Рис 2б
8. Перенесем цикл с новыми значениями (рис. 2б) в новую матрицу (табл. 13) и заполним таблицу поставками, не использованными в цикле.
Таблица 13
-
120
250
200
180
Вф
Ui
120
2
4
5
2
120
0
-5
-5
220
5
6
2
200
3
20
0
-4
300
4
120
3
80
6
7
40
0
60
0
170
6
2
170
6
6
0
-1
Vj
4
3
6
7
0
Оценки свободных клеток матрицы (табл. 13) не отрицательны, т.е. Еij
Е11 > 0; E12 > 0; E1ф > 0; E21 > 0; E22 > 0;
E2ф > 0; E33 = 0; E41 > 0; E43 > 0; E44 = 0.
Задача решена.
9. Определяется значение целевой функции:
F = 2*120 + 2*200 + 3*20 + 4*120 + 3*80 + 7*40 + 2*170 = 2040 руб.
Варианты заданий по теме 4
Решить транспортную ЗЛП методом потенциалов, построив исходный опорный план способом минимального элемента.
Вариант 1
| ai bj | 80 | 60 | 170 | 80 |
| 110 | 8 | 1 | 9 | 7 |
| 190 | 4 | 6 | 2 | 12 |
| 90 | 6 | 5 | 8 | 9 |
Вариант 2
| ai bj | 30 | 70 | 90 | 110 |
| 50 | 3 | 8 | 10 | 5 |
| 150 | 1 | 4 | 6 | 2 |
| 100 | 3 | 1 | 9 | 7 |
Вариант 3
| ai bj | 15 | 7 | 14 | 62 |
| 51 | 24 | 19 | 23 | 15 |
| 19 | 14 | 21 | 15 | 16 |
| 28 | 10 | 9 | 6 | 11 |
Вариант 4
| ai bj | 25 | 135 | 40 | 100 |
| 100 | 5 | 2 | 1 | 1 |
| 110 | 3 | 7 | 5 | 5 |
| 90 | 6 | 5 | 4 | 4 |