Файл: Методические материалы по курсу экономикоматематическое моделирование.doc
Добавлен: 05.12.2023
Просмотров: 121
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема 2. Задачи линейного программирования (ЗЛП)
Пример задачи 1.
Решить ЗЛП графическим способом.
Требуется найти max L = x1 + 4x2,
при ограничениях
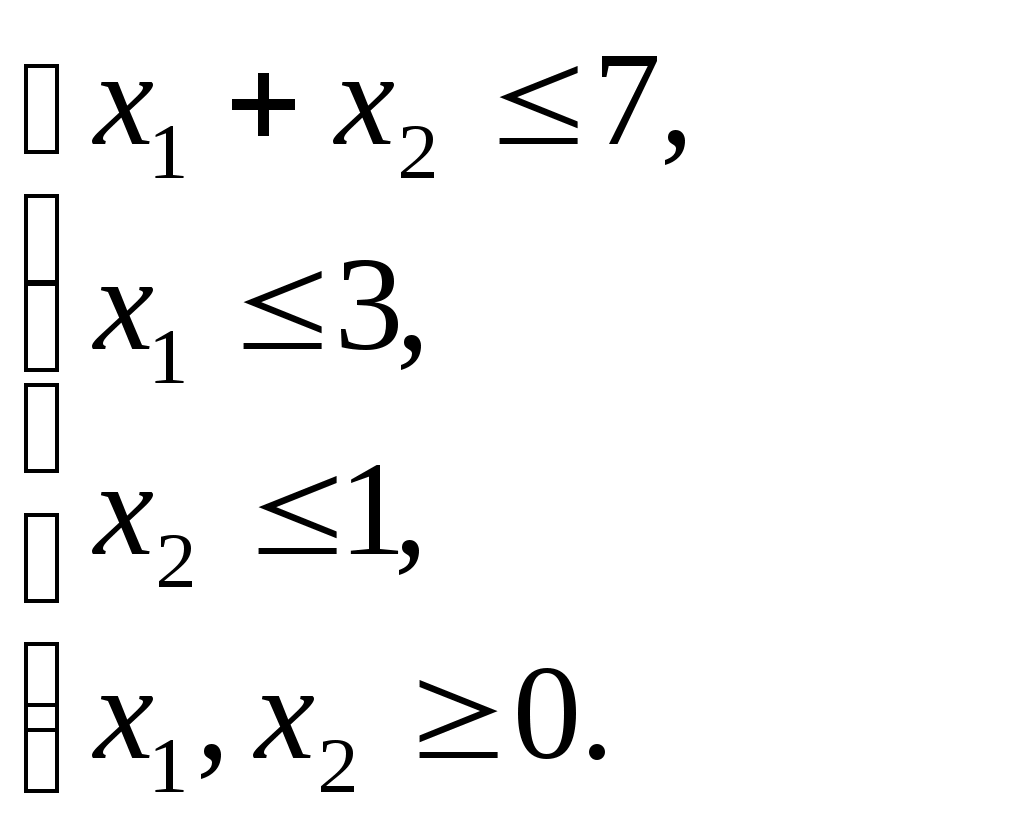
Решение задачи:
Запишем уравнения граничных прямых и построим их на плоскости x1ox2
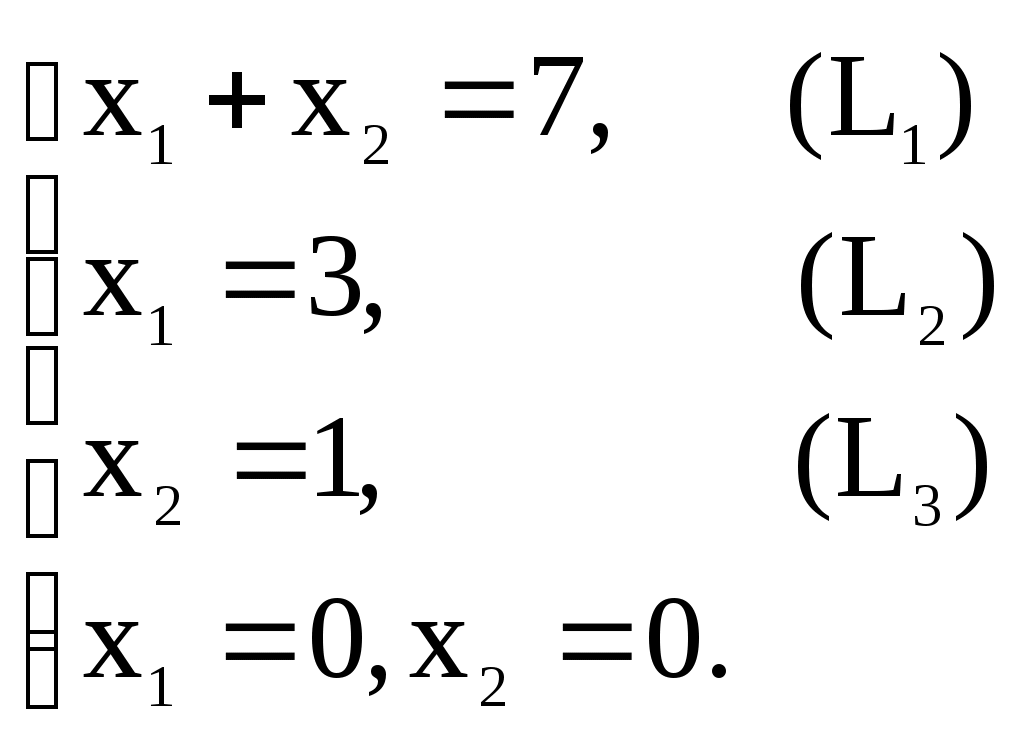
EMBED CorelDRAW.Graphic.11
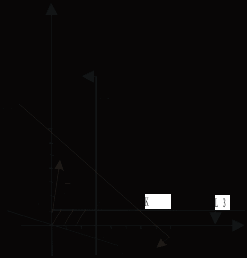
Рис. 1. Решение ЗЛП геометрическим способом
Выделив область решения каждого неравенства системы ограничений, получим многоугольник допустимых решений ЗЛП.
На рис. 1 видно, что областью допустимых решений является многоугольник ONAC.
Построим основную прямую L = 0, то есть x1 + 4x2 = 0, проходящую через начало координат O (0,0) перпендикулярно вектору
. Перемещая прямую L = 0 в направлении вектора , находим максимальную точку A, в которой пересекаются прямые L2 и L3, и координаты которой: x1 = 3, x2 = 1. Минимальной точкой является точка начала координат. Итак, Omin (0,0), Amax (3;1). Тогда Lmin = 0, Lmax = 7
Пример задачи 2. Решить ЗЛП симплексным методом
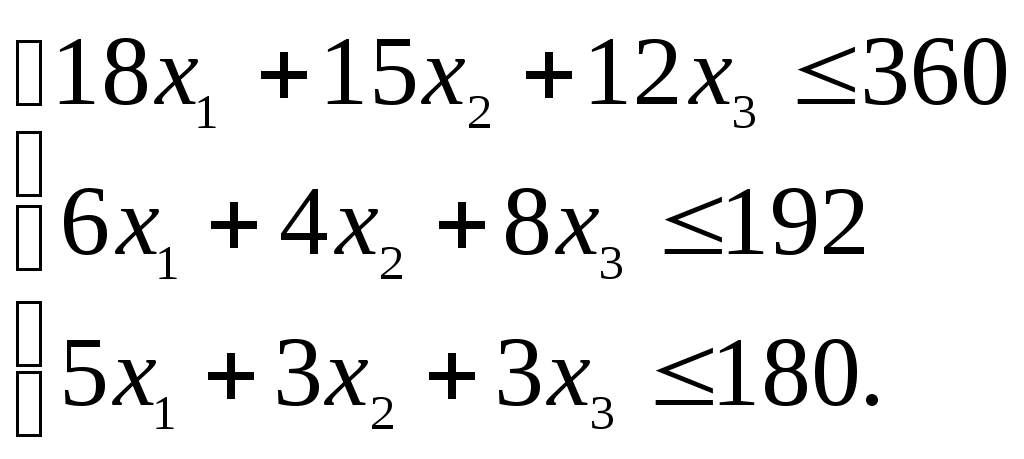х1
0; х2 0; х3 0.Решение задачи:
Приведем данную ЗЛП к канонической форме. Запишем ограничения – неравенства в форме ограничений - равенств, для чего введем дополнительные переменные х4, х5, х6:
18х1 + 15х2
+ 12х3 + х4 = 360,
6х1 + 4х1 + 8х3 + х5 = 192,
5х1 + 3х2 + 3х3 +х6 = 180,
Составим симплекс – таблицу (табл. 11).
В табл. 11 (итерация 0) имеем базисное решение Б1 (0; 0; 0; 360; 192; 180). Данное решение не оптимально, т.к. при F
max коэффициенты в строке оценок целевой функции должны быть положительны – условие оптимальности задачи.Исключаем переменные, содержащие в строке оценок F отрицательные коэффициенты. Допустим, это будет переменная х3. Для выбора разрешающего элемента (с целью получения неотрицательных решений) используется правило симплекс – преобразования: для всех положительных элементов столбца исключаемой переменной х3 вычисляется отношение свободного члена строки к ним самим, т.е bi/aij. Выбирается наименьшее из отношений, а соответствующий ему коэффициент aij - за разрешающий элемент.
Таблица 11
| Итерация | Базис | х1 х2 х3 х4 х5 х6 | bi | bi/aij |
| 0 | x4 x 5 x 6 | 18 15 12 1 0 0 6 4 8 0 1 0 5 3 3 0 0 1 | 360 192 180 | 30 24 60 |
| F | -9 -10 -16 0 0 0 | 0 | | |
| 1 | x 4 x 3 x 6 | 9 9 0 1 -12/8 0 6/8 4/8 1 0 1/8 0 22/8 12/8 0 0 3/8 1 | 72 24 108 | 8 48 72 |
| F | 3 -2 0 0 2 0 | 384 | | |
| 2 | x 2 x 3 x 6 | 1 1 0 1/9 -1/6 0 1/4 0 1 -1/18 57/72 0 5/4 0 0 -1/6 117/72 1 | 8 20 96 | |
| F | 5 0 0 2/9 11 0 |
1 2 3 4 5 6 7 8 9 10
|
Варианты заданий по теме 2
Вариант 1
Задача 1. Решить графическим методом следующую ЗЛП:
Z = x1 - 3x2 → max
x1 – x2 ≤ 3
2x1 + x2 ≥ 3
x1 – 3x2 ≤ 1
x1 ≥0, x2 ≥0
Задача 2. Решить ЗЛП симплексным методом.
Z = x1 + 3x2 + x3 → ––max
-x1 + x2 + x3 ≤ 1
x1 + x2 + x3 ≤ 4
x1 ≥0, x2 ≥0, x3 ≥0
Вариант 2
Задача 1. Решить графическим методом следующую ЗЛП:
Z = 3x1 + 5x2 → max
x1 + x2 ≤ 5
3x1 – x2 ≤ 3
x1 ≥0, x2 ≥0
Задача 2. Решить ЗЛП симплексным методом
Z = 4x1 + 3x2 → max
-x1 + 3x2 ≤ 9
2x1 + 3x2 ≤ 18
2x1 – x2 ≤ 10
x1 ≥0, x2 ≥0
Вариант 3
Задача 1. Решить графическим методом следующую ЗЛП:
Z = 2x1 + 2x2 → min
x1 + 3x2 ≥ 3
-2x1 + x2 ≤ 2
x1 + x2 ≤ 5
x1 ≥0, x2 ≥0
Задача 2. Решить ЗЛП симплексным методом
Z = 2x1 + x2 + 2x3 → max
3x1 + 2x2 + x3 ≤ 6
x1 + x2 + 2 x3 ≤ 4
x1 ≥0, x2 ≥0, x3 ≥0
Вариант 4
Задача 1. Решить графическим методом следующую ЗЛП:
Z = 2x1 + 2x2 → max
x1 + 3x2 ≥ 3
-2x1 + x2 ≤ 2
x1 + x2 ≤ 5
x1 ≥0, x2 ≥0
Задача 2. Решить ЗЛП симплексным методом.
Z = 5x1 + 4x2 - x3 → max
x1 – 2x2 + 2x3 ≤ 20
x1 + 4x2 – x3 ≤ 16
x1 ≥0, x2 ≥0, x3 ≥0
Вариант 5
Задача 1. Решить графическим методом следующую ЗЛП:
Z = 2x1 + 3x2 → min
x1 + x2 ≤ 4
6x1 + 2x2 ≥ 6
x1 + 5x2 ≥ 5
x1 ≥0, x2 ≥0
Задача 2. Решить ЗЛП симплексным методом.
Z = 4x1 - x2 + x3 → max
x1 + 2x2 + x3 ≤ 20
2x1 – x2 + 2 x3 ≤ 10
x1 ≥0, x2 ≥0, x3 ≥0
Вариант 6
Задача 1. Решить графическим методом следующую ЗЛП:
Z = –2x1 + x2 → min
x1 – x2 ≤ 3
x1 + x2 ≤ 9
-x1 + x2 ≥ 3
x1 + x2 ≥ 3/2
x1 ≥0, x2 ≥0
Задача 2. Решить ЗЛП симплексным методом.
Z = 3x1 + 5x2 → min
x1 + x2 ≤ 5
3x1 – x2 ≤ 3
x1 ≥0, x2 ≥0
Вариант 7
Задача 1. Решить графическим методом следующую ЗЛП:
Z = 4x1 + 3x2 → max
-x1 + 3x2 ≤ 9
2x1 + 3x2 ≤ 18
2x1 – x2 ≤ 10
x1 ≥0, x2 ≥0
Задача 2. Решить ЗЛП симплексным методом.
Z = 3x1 + x2 + 3x3 → max
x1 + 3x2 + 5x3 ≤ 9
2x1 + 2x2 + x3 ≤ 5
x1 ≥0, x2 ≥0, x3 ≥0
Вариант 8
Задача 1. Решить графическим методом следующую ЗЛП:
Z = x1 + x2 → max
-x1 + x2 ≤ 1
x1 + 2x2 ≤ 10
x1 + 2x2 ≥ 2
2x1 + x2 ≤ 10
x1 ≥0, x2 ≥0
Задача 2. Решить ЗЛП симплексным методом.
Z = x1 + x2 + x3 → max
2x1 + x2 + x3 ≤ 2
4x1 + 2x2 + x3 ≤ 2
x1 ≥0, x2 ≥0, x3 ≥0
Вариант 9
Задача 1. Решить графическим методом следующую ЗЛП:
Z = 3x1 + 5x2 → min
x1 + x2 ≤ 5
3x1 – x2 ≤ 3
x1 ≥0, x2 ≥0
Задача 2. Решить ЗЛП симплексным методом
Z = 5x1 + 4x2 + x3 → max
x1 + 4x2 + 2x3 ≤ 8
2x1 + x2 + x3 ≤ 4
x1 ≥0, x2 ≥0, x3 ≥0
Вариант 10
Задача 1. Решить графическим методом следующую ЗЛП:
Z = 2x1 + x2 → max
x1 + x2 ≤ 8
3x1 – 2x2 ≤ 12
-x1 + 2x2 ≤ 8
2x1 + 3x2 ≥ 6
x1 ≥0, x2 ≥0
Задача 2. Решить ЗЛП симплексным методом.
Z = 2x1 + x2 + x3 → max
x1 + x2 + x3 ≤ 6
2x1 - x2 + x3 ≤ 2
x1 ≥0, x2 ≥0, x3 ≥0
Тема 3. Двойственная задача линейного программирования
Пример задачи. По исходной задаче требуется построить двойственную.
Исходная задача: L = 10x1 + 6x2 – 4x3 →max
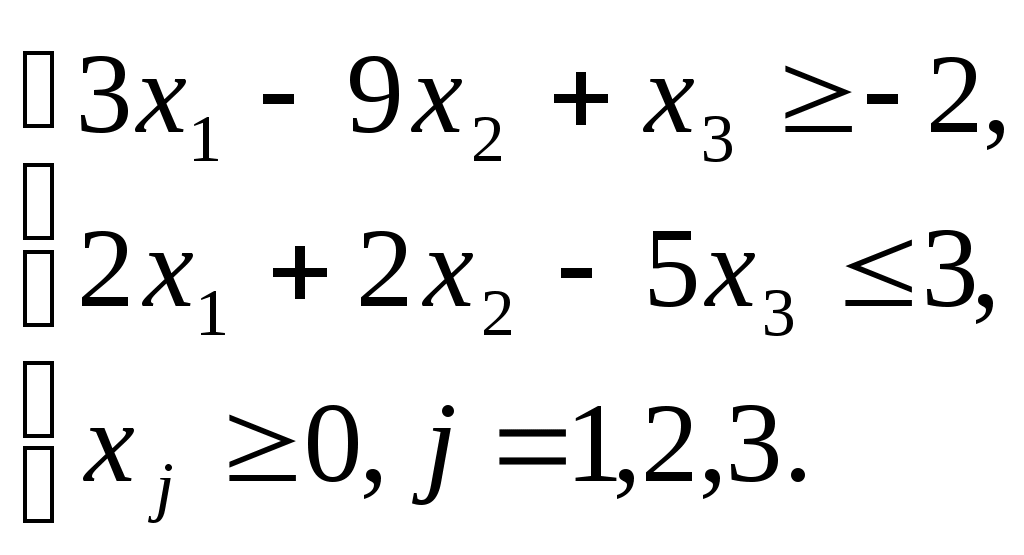
Решение задачи:
Приведем все неравенства системы ограничений исходной задачи к одному знаку:
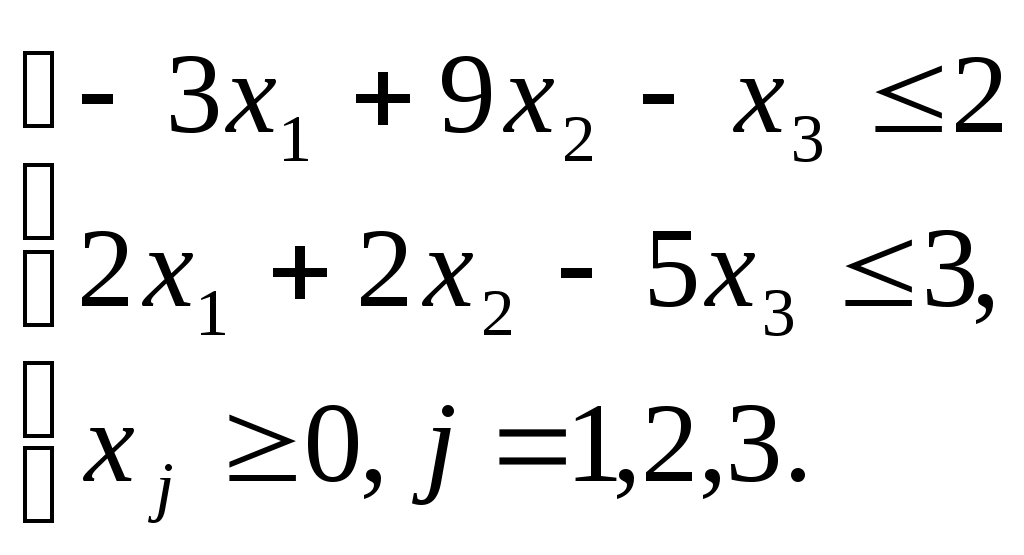
Двойственная задача.
