ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 311
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
фактических значений экономической рентабельности активов (ЭРi) на соответствующие вероятности (Рi):
.
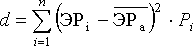Средневзвешенную дисперсию по правилам математической статистики устанавливают по формуле:
,
где d - параметр средневзвешенной дисперсии, %;
ЭРi– экономическая рентабельность актива i-го вида, %;
ЭРа– среднее значение экономической рентабельности активов, %;
Рi - значение вероятности получения дохода по активу i-го вида, доли единицы.
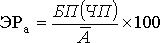Экономическую рентабельность активов (ЭРа) вычисляют по формуле:
,
где БП(ЧП) - бухгалтерская, или чистая, прибыль в расчетном периоде; Д
- средняя стоимость активов в данном периоде.
Стандартное отклонение вычисляют как квадратный корень из сред-
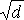невзвешенной дисперсии ( ). Чем выше будет полученный результат, тем более рисковым считают соответствующий актив (проект).
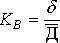Коэффициент вариации (Кв)позволяет оценить уровень риска, если показатели средних ожидаемых доходов по активу (проекту) отличаются между собой:
,
где Кв - коэффициент вариации, доли единицы;
δ - показатель средне-квадратического (стандартного) отклонения;
Д - средний ожидаемый доход (чистые денежные поступления, NPV) по активу (проекту).
При сравнении активов (реальных или финансовых) предпочтение отдают тому из них, по которому значение К
в самое минимальное, что свидетельствует о наиболее благоприятном соотношении риска и дохода.
Статический метод расчета уровня риска требует наличия большого объема информации, которая не всегда имеется у инвестора (инициатора проекта).
Анализ целесообразности затрат ориентирован на выявление потенциальных зон риска. Перерасход инвестиционных затрат по сравнению с параметрами проекта может быть вызван следующими причинами:
Эти ключевые факторы могут быть детализированы с целью определения уровня риска осуществляемых капитальных вложений.
Экспертный метод оценки инвестиционных рисков.
Экспертный метод применяется, когда специалисты оценивают вероятность потерь в трёх характерных точках риска: допустимых, критических и катастрофических потерь. Происходит обработка их мнений о величине риска. Используется при отсутствии большого количества данных. Недостаток этого метода заключается в том, что на исходный результат оценки оказывает влияние индивидуальных особенностей эксперта, его субъективность.
Метод экспертных оценок
применяется в случаях, когда:
З) входная информация неполная и невозможно предсказать влияние всех факторов;
4) возникли экстремальные ситуации, когда требуется принятие быстрых решений. Суть экспертных методов заключается в организованном сборе суждений и предположений экспертов с последующей обработкой полученных ответов и формированием результатов 9, с. 264.
Существует масса методов получения экспертных оценок. В одних с каждым экспертом работают отдельно, он даже не знает, кто еще является экспертом, а потому высказывает свое мнение независимо от авторитетов.
В других - экспертов собирают вместе, при этом эксперты обсуждают проблему друг с другом, учатся друг у друга, и неверные мнения отбрасываются. В одних методах число экспертов фиксировано, в других - число экспертов растет в процессе проведения экспертизы.
Среди наиболее распространенных методов получения экспертных оценок можно выделить: метод «Дельфы»; метод «снежного кома»; метод
«дерева целей»; метод «комиссий круглого стола»; метод эвристического прогнозирования; матричный метод.
Расчётно-аналитический (комбинированный) метод оценки инвестиционных рисков.
В расчётно-аналитическом методе приходится работать со статистическими данными, как и в
статистическом методе. Но здесь не сравниваются данные прошлых проектов, а производятся вычисления, определяющие показатели, которыми можно измерить степень риска. Эти показатели принадлежат теории вероятности. Количественная оценка вероятности наступления отдельных рисков и то, во что они могут обойтись, позволяет лицу, принимающему решение, выявить наиболее вероятные по возникновению и весомые по величине потерь риски, которые будут являться объектом рассмотрения и анализа для принятия решения о целесообразности принятия проекта. Кроме того, оценка вероятности поможет уяснить практические возможности исследований и дать прогноз будущих действий.
Применительно к экономическим задачам метод математической статистики сводится к систематизации, обработке и использовании статистических данных для научных и практических выводов. Основной элемент исследования – это анализ и построение взаимосвязей экономических переменных. Изучение этих взаимосвязей осложнено тем, что они не являются строгими, функциональными зависимостями. Иногда бывает трудно определить все основные факторы, влияющие на данную переменную (в том числе и риск), так как некоторые являются случайными и носят неопределённый характер или число статистических наблюдений является ограниченным. В таких условиях математическая статистика позволяет строить экономические модели и сравнивать их параметры, что в конечном итоге служит основой для экономического анализа и прогнозирования 12, с. 432.
Теория вероятностей
играет важную роль при статистических исследованиях вероятностно-случайных явлений. Недостаток статистического подхода заключается в том, что он основывается на имеющихся статистических данных прошлых периодов, в то время как оценка риска относится к будущим
событиям. Быстро меняющаяся экономическая обстановка снижает ценность данного подхода. В то же время его достоинством является объективность.
Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения какого-нибудь критерия варианта использования имеющихся ресурсов, называются оптимизационными. Оптимизационные задачи решаются с помощью оптимизационных моделей методами математического программирования. Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющих эту область 8, с. 214.
Целевая функция в самом общем виде, в свою очередь, тоже состоит из трёх элементов: управляемых переменных; неуправляемых переменных; формы функции (вида зависимости между ними).
Изучение данной задачи и служит инструментом анализа и принятия правильного решения в условиях постоянно меняющейся экономической ситуации.
.
Средневзвешенную дисперсию по правилам математической статистики устанавливают по формуле:,
где d - параметр средневзвешенной дисперсии, %;
ЭРi– экономическая рентабельность актива i-го вида, %;
ЭРа– среднее значение экономической рентабельности активов, %;
Рi - значение вероятности получения дохода по активу i-го вида, доли единицы.
Экономическую рентабельность активов (ЭРа) вычисляют по формуле:,
где БП(ЧП) - бухгалтерская, или чистая, прибыль в расчетном периоде; Д
- средняя стоимость активов в данном периоде.
Стандартное отклонение вычисляют как квадратный корень из сред-
невзвешенной дисперсии ( ). Чем выше будет полученный результат, тем более рисковым считают соответствующий актив (проект). Коэффициент вариации (Кв)позволяет оценить уровень риска, если показатели средних ожидаемых доходов по активу (проекту) отличаются между собой:,
где Кв - коэффициент вариации, доли единицы;
δ - показатель средне-квадратического (стандартного) отклонения;
Д - средний ожидаемый доход (чистые денежные поступления, NPV) по активу (проекту).
При сравнении активов (реальных или финансовых) предпочтение отдают тому из них, по которому значение К
в самое минимальное, что свидетельствует о наиболее благоприятном соотношении риска и дохода.
Статический метод расчета уровня риска требует наличия большого объема информации, которая не всегда имеется у инвестора (инициатора проекта).
Анализ целесообразности затрат ориентирован на выявление потенциальных зон риска. Перерасход инвестиционных затрат по сравнению с параметрами проекта может быть вызван следующими причинами:
-
изменением границ проектирования; -
возникновением дополнительных затрат у подрядчика в ходе строительства объекта; -
первоначальной недооценкой стоимости проекта; -
различием в производительности (например, в продуктивности нефтяных и газовых скважин); -
несовпадением в эффективности проектов (доходности, окупаемости капиталовложений, безопасности) и т. д. 1, с. 280.
Эти ключевые факторы могут быть детализированы с целью определения уровня риска осуществляемых капитальных вложений.
Экспертный метод оценки инвестиционных рисков.
Экспертный метод применяется, когда специалисты оценивают вероятность потерь в трёх характерных точках риска: допустимых, критических и катастрофических потерь. Происходит обработка их мнений о величине риска. Используется при отсутствии большого количества данных. Недостаток этого метода заключается в том, что на исходный результат оценки оказывает влияние индивидуальных особенностей эксперта, его субъективность.
Метод экспертных оценок
применяется в случаях, когда:
-
длина исходных динамических рядов недостаточна для оценивания с использованием экономико-статистических методов; -
связь между исследуемыми явлениями носит качественный характер и не может быть выражена с помощью традиционных количественных измерителей;
З) входная информация неполная и невозможно предсказать влияние всех факторов;
4) возникли экстремальные ситуации, когда требуется принятие быстрых решений. Суть экспертных методов заключается в организованном сборе суждений и предположений экспертов с последующей обработкой полученных ответов и формированием результатов 9, с. 264.
Существует масса методов получения экспертных оценок. В одних с каждым экспертом работают отдельно, он даже не знает, кто еще является экспертом, а потому высказывает свое мнение независимо от авторитетов.
В других - экспертов собирают вместе, при этом эксперты обсуждают проблему друг с другом, учатся друг у друга, и неверные мнения отбрасываются. В одних методах число экспертов фиксировано, в других - число экспертов растет в процессе проведения экспертизы.
Среди наиболее распространенных методов получения экспертных оценок можно выделить: метод «Дельфы»; метод «снежного кома»; метод
«дерева целей»; метод «комиссий круглого стола»; метод эвристического прогнозирования; матричный метод.
Расчётно-аналитический (комбинированный) метод оценки инвестиционных рисков.
В расчётно-аналитическом методе приходится работать со статистическими данными, как и в
статистическом методе. Но здесь не сравниваются данные прошлых проектов, а производятся вычисления, определяющие показатели, которыми можно измерить степень риска. Эти показатели принадлежат теории вероятности. Количественная оценка вероятности наступления отдельных рисков и то, во что они могут обойтись, позволяет лицу, принимающему решение, выявить наиболее вероятные по возникновению и весомые по величине потерь риски, которые будут являться объектом рассмотрения и анализа для принятия решения о целесообразности принятия проекта. Кроме того, оценка вероятности поможет уяснить практические возможности исследований и дать прогноз будущих действий.
Применительно к экономическим задачам метод математической статистики сводится к систематизации, обработке и использовании статистических данных для научных и практических выводов. Основной элемент исследования – это анализ и построение взаимосвязей экономических переменных. Изучение этих взаимосвязей осложнено тем, что они не являются строгими, функциональными зависимостями. Иногда бывает трудно определить все основные факторы, влияющие на данную переменную (в том числе и риск), так как некоторые являются случайными и носят неопределённый характер или число статистических наблюдений является ограниченным. В таких условиях математическая статистика позволяет строить экономические модели и сравнивать их параметры, что в конечном итоге служит основой для экономического анализа и прогнозирования 12, с. 432.
Теория вероятностей
играет важную роль при статистических исследованиях вероятностно-случайных явлений. Недостаток статистического подхода заключается в том, что он основывается на имеющихся статистических данных прошлых периодов, в то время как оценка риска относится к будущим
событиям. Быстро меняющаяся экономическая обстановка снижает ценность данного подхода. В то же время его достоинством является объективность.
Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения какого-нибудь критерия варианта использования имеющихся ресурсов, называются оптимизационными. Оптимизационные задачи решаются с помощью оптимизационных моделей методами математического программирования. Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющих эту область 8, с. 214.
Целевая функция в самом общем виде, в свою очередь, тоже состоит из трёх элементов: управляемых переменных; неуправляемых переменных; формы функции (вида зависимости между ними).
Изучение данной задачи и служит инструментом анализа и принятия правильного решения в условиях постоянно меняющейся экономической ситуации.
- Анализ и оценка рисков реальных инвестиций на примере ООО «Рубин»