Файл: Это временное предприятие, предназначенное для создания.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 115
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Основные положения системы управления проектами
Процессы управления проектами могут быть разбиты на шесть основных групп:
О сновные процессы планирования
Вспомогательные процессы планирования
Временная стоимость денег (прошу прощения за теорию)
Доходность рыночная, предприятия и проекта
Риск рынка, предприятия и проекта
Пример: инвестируем 100 рублей.
Чтобы определить прибыль, бросаем две монетки.
FV также называют наращенным значением.
На следующем этапе рассмотрим, как вычислять наращенное значение, если средства инвестируются не на один период, а больше или меньше.
Во-первых, необходимо сделать одно важное замечание. Когда мы вычисляли доходность, мы не определяли, чему равен период инвестирования. Он может быть равен году, больше или меньше. Для удобства сравнения различных проектов между собой используют годовую доходность, т.е. доходность, рассчитанную на период равный одному году. Как быть, если период инвестирования не равен одному году? Вычислить, чему равен период инвестирования, если его измерять в годах. Тогда формулу для вычисления наращенной суммы можно записать в виде:
FV=PV+INT=PV+iгодn*PV=PV*(1+iгодn).
В этой формуле n означает количество лет в периоде инвестирования. Сама формула называется формулой простых процентов, т.к. предполагается, что доход начисляется только на инвестированную сумму. Конечно, в действительности никто не согласится, чтобы за несколько лет проценты начислялись только на первоначальную сумму. Как правило, формулу простых процентов используют для вычисления дохода, получаемого в течение короткого периода времени, как, например, несколько месяцев или даже дней.
В случае длинных периодов инвестирования используют другой подход, так называемые сложные или составные проценты.
Например, вы помещаете 100 рублей на срочный вклад в банк на 3 года под 10% годовых. В конце первого года сумма вырастет до 100(1+10%)=110 рублей, и за второй год вы снова должны будете получить 10% от суммы, которой вы располагали к началу второго года, т.е. от 110 рублей, поэтому к концу второго года у вас уже будет 110(1+10%)=121 рублей. Как видим, доход за второй год на 1 рубль превышает доход за первый год, потому что дополнительной заработали 10% на доход первого года. А к концу третьего года уже будет 121(1+10%)=133,10 рублей. Если бы мы использовали формулу простых процентов, то наращенное значение равнялось 100(1+3*10%)=130 рублей. Запишем полученные нами результаты в виде формул:
FV1 = PV (1+i)1 = 100 (1.10)1 = 110 рублей,
FV2 = PV (1+i)2 = 100 (1.10)2 = 121 рублей,
FV3 = PV (1+i)3 = 100 (1.10)3 = 133,10 рублей.
Этот процесс называется составлением. В общем виде формула для выражения наращенной суммы FVот текущего значения PVчерез n периодов может быть представлена следующим образом:
FVn = PV (1+i)n
В уравнении (1+i)n называют коэффициентом наращения денежных средств и он означает, на сколько увеличится за n лет значение одного инвестированного рубля, и обозначается FVIFi,n. Тогда уравнение может быть переписано в следующем виде:
FVn = PV (1+i)n = PV * FVIFi,n.
В вышеприведенном примере мы вычисляли некоторое значение инвестиций через определенное время и при заданной норме прибыли. Во многих случаях, нам, наоборот, необходимо знать текущую стоимость при условии, что через определенное время сумма станет равной заранее известной величине. К примеру, вам предлагается на выбор - 5000 рублей сегодня или 5100 рублей через год. Предположим, что некоторый надежный банк выплачивает 10% годовых. Что вы предпочтете 5000 рублей сейчас или 5100 рублей через год при отсутствии риска? Мы можем найти ответ, используя формулу для вычисления наращенной суммы. Если сегодня мы располагаем суммой PV=5000 рублей (в соответствии с первой альтернативой), то, поместив эти деньги в банк под 10% годовых мы получим наращенное значение 5000(1+10%)=5050 рублей, поэтому мы можем сказать, что предпочтительней выбрать вторую альтернативу – 5100 рублей через год. Эффективность выбора заключается в дополнительных 50 рублях (5100-5050).
Найти ответ можно и другим способом. Зададимся вопросом: какую сумму необходимо инвестировать сегодня, чтобы через год получить 5100 рублей? Для того, чтобы найти текущее значение величины в 5100 рублей мы должны выполнить следующие действия:
PV=5100/ FVIF10%,1
Для того чтобы найти текущее значение, мы разделили будущее значение на годовой коэффициент наращения, соответствующий банковской процентной ставке, чтобы найти значение будущих доходов в настоящий момент. Нахождение значения в настоящий момент называется дисконтированием, и это действие обратно действую наращения. Полученное таким образом текущее значение также называют приведенным значением. Формула для приведенного значения выглядит следующим образом:
PV = FV/ FVIFi,n = FV*PVIFi,n ,
где PVIFi,n = 1 /(1+i)n – коэффициент дисконтирования или приведения. PVIFi,n представляет собой текущее значение будущего значения равному 1 рублю через n периодов и при процентной ставке i. Таблица 2 в приложении содержит значения PVIFi,n для широкого диапазона i и
n.
Пример. Если вы хотите иметь 10,000 рублей через 5 лет, то какую сумму вы должны будете поместить на депозит в банк, который выплачивает 12% ежегодно.
PV = FV /(1+i)n = 10,000/(1+ 0,12)5 = 5.6724,27
Итак, если мы знаем текущее значение и процентную ставку, то мы можем вычислить наращенное значение. И наоборот, если мы знаем количество денежных средств в некоторый момент в будущем, то дисконтируя, мы можем определить их значение в настоящий момент времени.
В формулах для нахождения текущего (дисконтированного) и будущего значений присутствуют четыре переменные PV, FV, i, n и необходимо знать значения трех из них, чтобы определить четвертую. Мы видоизменяли формулу сложных процентов для нахождения денежных значений. Аналогично мы можем выразить процентную ставку или временной период для нахождения через три остальных.
Для нахождения процентной ставки:
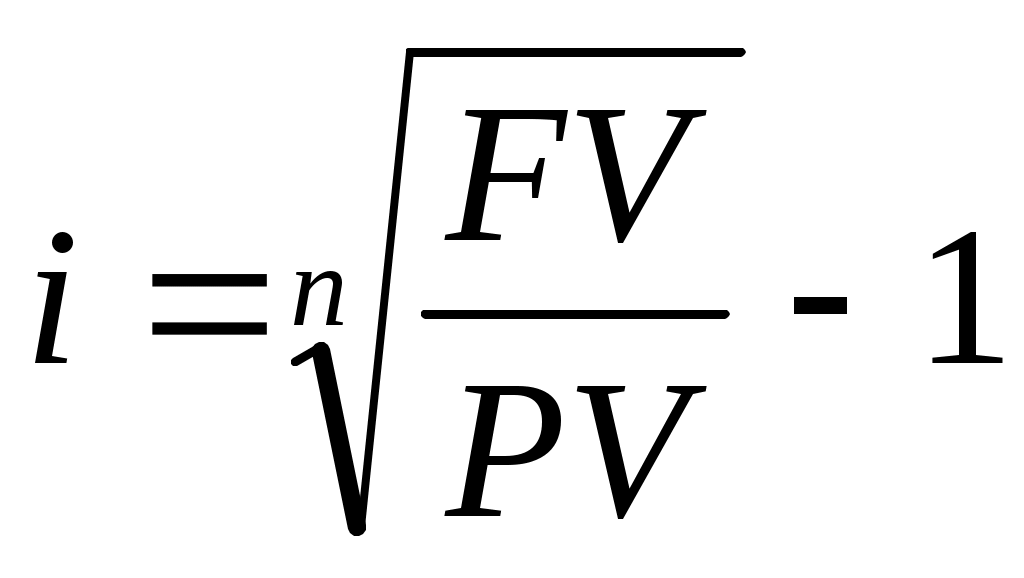 .
.
Для нахождения периода времени
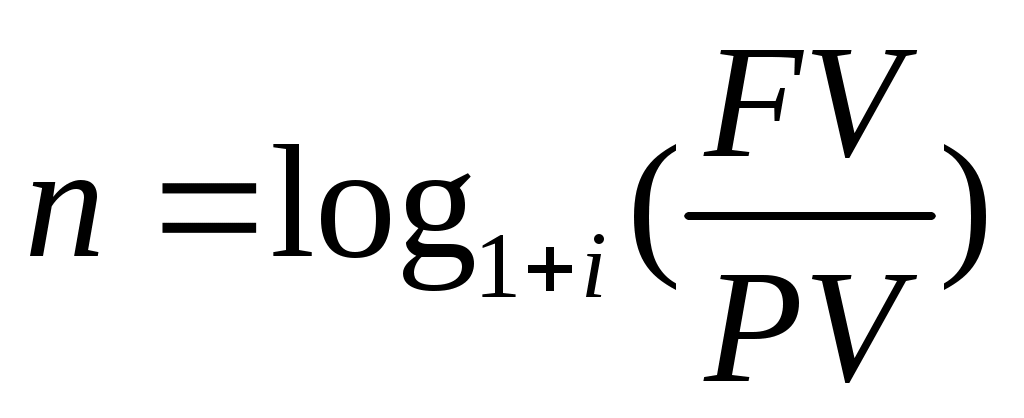 .
.
Конечно, найти доходность или период времени не так легко, как текущее или будущее значение.
Что брать в качестве процентной ставки?
Стоимость капитала – это стоимость, выраженная в процентах, привлечения денежных средств, необходимых для функционирования предприятия.
Стоимость заемного капитала – ставка кредитования.
Стоимость собственного капитала?
Норма отсечения – максимально допустимая стоимость капитала, или минимально возможная доходность операций предприятия.
ЧДДА=
ЧДДВ=
ЧДДС=
ВНДА=
ВНДВ=
ВНДС=
Сложные инвестиции
В большинстве случаев инвестиции представляют собой не единовременный акт, а несколько действий по приобретению и замене оборудования, увеличению оборотного капитала. Эти факторы усложняют процесс бюджетирования и выявления объема необходимых инвестиций.
Оборотный капитал – это разность между текущими активами и краткосрочной задолженностью. Опыт свидетельствует
, что оборотный капитал должен составлять около 20% от объема продаж.
В отличие от основных средств, которые амортизируются, и чья остаточная стоимость может снижаться до нуля. Оборотный капитал не уменьшается, он должен сохранять свои первоначальные размеры.
Пример. Инвестиции в новый продукт рассчитаны на пять лет. Объемы продаж оцениваются в 20.000 руб. ежегодно. Затраты составляют 6000 рублей ежегодно. Требуемые инвестиции: 30.000 рублей на приобретение нового оборудования и35.000 рублей в оборотный капитал. Полагаем, что амортизация производится по линейному методу, остаточная стоимость равна нулю, стоимость капитала составляет 12%. Величина подоходного налога – 40%.
Тогда ежегодные денежные потоки с 1 по 5 года будут следующими:
Вычисление налогов Денежные потоки
Объем реализации 20000 20000
Затраты (переменные и постоянные) 6000 6000
Денежные потоки до уплаты налогов 14000 14000
Амортизация (30000 руб./5 лет) 6000
Снижение налогооблагаемой базы 8000
Налоги (40%) 3200 3200
Чистая прибыль в год 10800
Конец 5 года:
Возврат оборотного капитала 35000
Вычисление чистого дисконтированного дохода:
Дисконтированный доход за 5 лет (10800*3,605) 38934
Приведенное значение возвращенного
оборотного капитала (35000 * 0,567) 19845
Общий дисконтированный доход 58779
Необходимые инвестиции 30000+35000 65000
ЧДД -6221
А что было, если бы мы не учитывали оборотный капитал?
Два подхода:
Инкрементальный – рассматривает разницу в денежных потоках рассматриваемых альтернатив
Проектный – рассматривает ЧДД каждой из альтернатив.
Оба подхода приводят к одному и тому же результату, поэтому на выбор может влиять только удобство вычислений.
Пример. Предположим, предприятие имеет оборудование, которое было приобретено пять лет назад за 100.000 рублей. Дополнительно известно:
Оставшийся срок эксплуатации 5 лет.
Остаточная стоимость на сегодня 50000 руб.
Амортизация 10000 руб.
Цена реализации – сегодня 20000 руб.
– через пять лет 10000 руб.
Ежегодные затраты на обслуживание 30000 руб.
Предположим, что на рынке появилось новое оборудование стоимостью 60000 рублей, сроком эксплуатации 5 лет, нулевой остаточной стоимостью и затратами на обслуживание 15000 рублей в год. Норма отсечения составляет 16%. Имеет ли смысл заменять оборудование?
Рассмотрим первоначальные инвестиции.
Вычисление налогов Денежные потоки
Приобретение оборудования 60000
На следующем этапе рассмотрим, как вычислять наращенное значение, если средства инвестируются не на один период, а больше или меньше.
Во-первых, необходимо сделать одно важное замечание. Когда мы вычисляли доходность, мы не определяли, чему равен период инвестирования. Он может быть равен году, больше или меньше. Для удобства сравнения различных проектов между собой используют годовую доходность, т.е. доходность, рассчитанную на период равный одному году. Как быть, если период инвестирования не равен одному году? Вычислить, чему равен период инвестирования, если его измерять в годах. Тогда формулу для вычисления наращенной суммы можно записать в виде:
FV=PV+INT=PV+iгодn*PV=PV*(1+iгодn).
В этой формуле n означает количество лет в периоде инвестирования. Сама формула называется формулой простых процентов, т.к. предполагается, что доход начисляется только на инвестированную сумму. Конечно, в действительности никто не согласится, чтобы за несколько лет проценты начислялись только на первоначальную сумму. Как правило, формулу простых процентов используют для вычисления дохода, получаемого в течение короткого периода времени, как, например, несколько месяцев или даже дней.
В случае длинных периодов инвестирования используют другой подход, так называемые сложные или составные проценты.
Например, вы помещаете 100 рублей на срочный вклад в банк на 3 года под 10% годовых. В конце первого года сумма вырастет до 100(1+10%)=110 рублей, и за второй год вы снова должны будете получить 10% от суммы, которой вы располагали к началу второго года, т.е. от 110 рублей, поэтому к концу второго года у вас уже будет 110(1+10%)=121 рублей. Как видим, доход за второй год на 1 рубль превышает доход за первый год, потому что дополнительной заработали 10% на доход первого года. А к концу третьего года уже будет 121(1+10%)=133,10 рублей. Если бы мы использовали формулу простых процентов, то наращенное значение равнялось 100(1+3*10%)=130 рублей. Запишем полученные нами результаты в виде формул:
FV1 = PV (1+i)1 = 100 (1.10)1 = 110 рублей,
FV2 = PV (1+i)2 = 100 (1.10)2 = 121 рублей,
FV3 = PV (1+i)3 = 100 (1.10)3 = 133,10 рублей.
Этот процесс называется составлением. В общем виде формула для выражения наращенной суммы FVот текущего значения PVчерез n периодов может быть представлена следующим образом:
FVn = PV (1+i)n
В уравнении (1+i)n называют коэффициентом наращения денежных средств и он означает, на сколько увеличится за n лет значение одного инвестированного рубля, и обозначается FVIFi,n. Тогда уравнение может быть переписано в следующем виде:
FVn = PV (1+i)n = PV * FVIFi,n.
В вышеприведенном примере мы вычисляли некоторое значение инвестиций через определенное время и при заданной норме прибыли. Во многих случаях, нам, наоборот, необходимо знать текущую стоимость при условии, что через определенное время сумма станет равной заранее известной величине. К примеру, вам предлагается на выбор - 5000 рублей сегодня или 5100 рублей через год. Предположим, что некоторый надежный банк выплачивает 10% годовых. Что вы предпочтете 5000 рублей сейчас или 5100 рублей через год при отсутствии риска? Мы можем найти ответ, используя формулу для вычисления наращенной суммы. Если сегодня мы располагаем суммой PV=5000 рублей (в соответствии с первой альтернативой), то, поместив эти деньги в банк под 10% годовых мы получим наращенное значение 5000(1+10%)=5050 рублей, поэтому мы можем сказать, что предпочтительней выбрать вторую альтернативу – 5100 рублей через год. Эффективность выбора заключается в дополнительных 50 рублях (5100-5050).
Найти ответ можно и другим способом. Зададимся вопросом: какую сумму необходимо инвестировать сегодня, чтобы через год получить 5100 рублей? Для того, чтобы найти текущее значение величины в 5100 рублей мы должны выполнить следующие действия:
PV=5100/ FVIF10%,1
Для того чтобы найти текущее значение, мы разделили будущее значение на годовой коэффициент наращения, соответствующий банковской процентной ставке, чтобы найти значение будущих доходов в настоящий момент. Нахождение значения в настоящий момент называется дисконтированием, и это действие обратно действую наращения. Полученное таким образом текущее значение также называют приведенным значением. Формула для приведенного значения выглядит следующим образом:
PV = FV/ FVIFi,n = FV*PVIFi,n ,
где PVIFi,n = 1 /(1+i)n – коэффициент дисконтирования или приведения. PVIFi,n представляет собой текущее значение будущего значения равному 1 рублю через n периодов и при процентной ставке i. Таблица 2 в приложении содержит значения PVIFi,n для широкого диапазона i и
n.
Пример. Если вы хотите иметь 10,000 рублей через 5 лет, то какую сумму вы должны будете поместить на депозит в банк, который выплачивает 12% ежегодно.
PV = FV /(1+i)n = 10,000/(1+ 0,12)5 = 5.6724,27
Итак, если мы знаем текущее значение и процентную ставку, то мы можем вычислить наращенное значение. И наоборот, если мы знаем количество денежных средств в некоторый момент в будущем, то дисконтируя, мы можем определить их значение в настоящий момент времени.
В формулах для нахождения текущего (дисконтированного) и будущего значений присутствуют четыре переменные PV, FV, i, n и необходимо знать значения трех из них, чтобы определить четвертую. Мы видоизменяли формулу сложных процентов для нахождения денежных значений. Аналогично мы можем выразить процентную ставку или временной период для нахождения через три остальных.
Для нахождения процентной ставки:
Для нахождения периода времени
Конечно, найти доходность или период времени не так легко, как текущее или будущее значение.
Рассмотрим пример
| Период | 0 | 1 | 2 | 3 | 4 |
| Инвестиция А | -800 | 600 | 200 | 150 | -80 |
| Инвестиция В | -700 | 300 | 400 | 30 | 100 |
| Инвестиция С | -400 | -200 | 700 | 0 | 0 |
| Коэффициент дисконтирования | | | | | |
| Инвестиция А | | | | | |
| Инвестиция В | | | | | |
| Инвестиция С | | | | | |
Что брать в качестве процентной ставки?
Стоимость капитала и норма отсечения
Стоимость капитала – это стоимость, выраженная в процентах, привлечения денежных средств, необходимых для функционирования предприятия.
Стоимость заемного капитала – ставка кредитования.
Стоимость собственного капитала?
Норма отсечения – максимально допустимая стоимость капитала, или минимально возможная доходность операций предприятия.
ЧДДА=
ЧДДВ=
ЧДДС=
ВНДА=
ВНДВ=
ВНДС=
Сложные инвестиции
В большинстве случаев инвестиции представляют собой не единовременный акт, а несколько действий по приобретению и замене оборудования, увеличению оборотного капитала. Эти факторы усложняют процесс бюджетирования и выявления объема необходимых инвестиций.
Изменения в оборотном капитале
Оборотный капитал – это разность между текущими активами и краткосрочной задолженностью. Опыт свидетельствует
, что оборотный капитал должен составлять около 20% от объема продаж.
В отличие от основных средств, которые амортизируются, и чья остаточная стоимость может снижаться до нуля. Оборотный капитал не уменьшается, он должен сохранять свои первоначальные размеры.
Пример. Инвестиции в новый продукт рассчитаны на пять лет. Объемы продаж оцениваются в 20.000 руб. ежегодно. Затраты составляют 6000 рублей ежегодно. Требуемые инвестиции: 30.000 рублей на приобретение нового оборудования и35.000 рублей в оборотный капитал. Полагаем, что амортизация производится по линейному методу, остаточная стоимость равна нулю, стоимость капитала составляет 12%. Величина подоходного налога – 40%.
Тогда ежегодные денежные потоки с 1 по 5 года будут следующими:
Вычисление налогов Денежные потоки
Объем реализации 20000 20000
Затраты (переменные и постоянные) 6000 6000
Денежные потоки до уплаты налогов 14000 14000
Амортизация (30000 руб./5 лет) 6000
Снижение налогооблагаемой базы 8000
Налоги (40%) 3200 3200
Чистая прибыль в год 10800
Конец 5 года:
Возврат оборотного капитала 35000
Вычисление чистого дисконтированного дохода:
Дисконтированный доход за 5 лет (10800*3,605) 38934
Приведенное значение возвращенного
оборотного капитала (35000 * 0,567) 19845
Общий дисконтированный доход 58779
Необходимые инвестиции 30000+35000 65000
ЧДД -6221
А что было, если бы мы не учитывали оборотный капитал?
Решения о замене оборудования
Два подхода:
Инкрементальный – рассматривает разницу в денежных потоках рассматриваемых альтернатив
Проектный – рассматривает ЧДД каждой из альтернатив.
Оба подхода приводят к одному и тому же результату, поэтому на выбор может влиять только удобство вычислений.
Пример. Предположим, предприятие имеет оборудование, которое было приобретено пять лет назад за 100.000 рублей. Дополнительно известно:
Оставшийся срок эксплуатации 5 лет.
Остаточная стоимость на сегодня 50000 руб.
Амортизация 10000 руб.
Цена реализации – сегодня 20000 руб.
– через пять лет 10000 руб.
Ежегодные затраты на обслуживание 30000 руб.
Предположим, что на рынке появилось новое оборудование стоимостью 60000 рублей, сроком эксплуатации 5 лет, нулевой остаточной стоимостью и затратами на обслуживание 15000 рублей в год. Норма отсечения составляет 16%. Имеет ли смысл заменять оборудование?
Рассмотрим первоначальные инвестиции.
Вычисление налогов Денежные потоки
Приобретение оборудования 60000