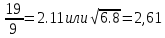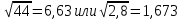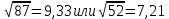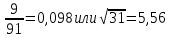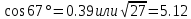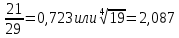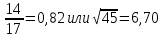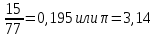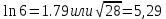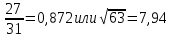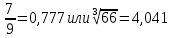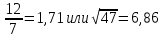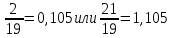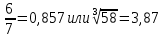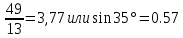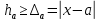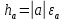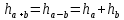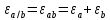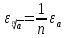Файл: Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 258
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
«Решение нелинейных уравнений»
«Решение систем линейных алгебраических уравнений»
«Метод прогонки для трехдиагональных систем»
« Использование итерационных численных методов для решения СЛАУ»
« Использование итерационных численных методов для решения СЛАУ»
«Численное решение алгебраических проблем собственных значений»
«Интерполирование. Интерполяционные формулы»
Интерполяционная схема Эйткена
« Интерполирование. Интерполяционные формулы»
«Аппроксимация, построение аппроксимирующих кривых»
«Численное дифференцирование функции. Методы дифференцирования»
Содержание
Содержание 1
Лабораторная работа №1. 3
«Основы теории погрешностей» 3
Лабораторная работа №2. 11
«Основы теории погрешностей» 11
Лабораторная работа №3-4. 19
«Решение нелинейных уравнений» 19
Лабораторная работа №5. 27
«Решение систем линейных алгебраических уравнений» 27
Лабораторная работа №6. 34
«Метод прогонки для трехдиагональных систем» 34
Лабораторная работа №7. 39
« Использование итерационных численных методов для решения СЛАУ» 39
Лабораторная работа №8. 47
« Использование итерационных численных методов для решения СЛАУ» 47
Лабораторная работа №9. 53
«Численное решение алгебраических проблем собственных значений» 53
Теоретический материал: 56
Степенной метод: 56
Метод скалярных произведений: 57
Метод вращений Якоби 58
Пример решение проблемы собственных значений в среде MatLab: 61
Лабораторная работа №10. 63
«Интерполирование. Интерполяционные формулы» 63
Интерполяционная схема Эйткена 64
Лабораторная работа №11. 68
« Интерполирование. Интерполяционные формулы» 68
Лабораторная работа №12. 75
«Аппроксимация, построение аппроксимирующих кривых» 75
Лабораторная работа 13. 82
«Численное дифференцирование функции. Методы дифференцирования» 82
Лабораторная работа №14. 88
« Численное интегрирование функции» 88
Лабораторная работа №15 95
«Численные методы решения дифференциальных уравнений» 95
Список использованной литературы 94
Лабораторная работа №1.«Основы теории погрешностей» 4
Лабораторная работа №2.«Основы теории погрешностей» 11
Лабораторная работа №3-4.«Решение нелинейных уравнений» 18
Лабораторная работа №5.«Решение систем линейных алгебраических уравнений» 25
Лабораторная работа №6.«Метод прогонки для трехдиагональных систем» 32
Лабораторная работа №7.« Использование итерационных численных методов для решения СЛАУ» 37
Лабораторная работа №8.« Использование итерационных численных методов для решения СЛАУ» 44
Лабораторная работа №9.«Численное решение алгебраических проблем собственных значений» 50
Лабораторная работа №10.«Интерполирование. Интерполяционные формулы» 59
Лабораторная работа №11.« Интерполирование. Интерполяционные формулы» 64
Лабораторная работа №12.«Аппроксимация, построение аппроксимирующих кривых» 70
Лабораторная работа 13.«Численное дифференцирование функции. Методы дифференцирования» 76
Лабораторная работа №14.« Численное интегрирование функции» 81
Лабораторная работа №15.«Численные методы решения дифференциальных уравнений» 88
Список использованной литературы 94
Лабораторная работа №1.
«Основы теории погрешностей»
Цель: Закрепление теоретического материала по теме значащие и верные цифры. Знакомство со средой MatLab 7.0.
Задание №1. Округлить сомнительные числа, оставив верные знаки в узком смысле. Определить абсолютную погрешность результата.
Варианты заданий:
-
9,86314 0,00074
0,00074 -
27,45456;
-
0,4239
-
13,15466;
-
75,5242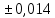
-
87,231;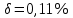
-
34,7856;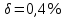
-
4,1236;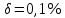
-
23,09870 0,0009
0,0009 -
3,41253 0,00023
0,00023 -
33,60457;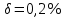
-
37,848 0,0079
0,0079 -
1,12486;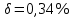
-
2,75387 0,00011
0,00011 -
5,75555;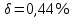
Задание 2. Округлить сомнительные цифры числа, оставив верные знаки в широком смысле. Определить абсолютную погрешность результата.
Варианты заданий:
-
29,7387 0,0013
0,0013 -
10,12486;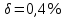
-
79,83014 0,00074
0,00074 -
5,75055;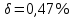
-
23,0981 0,0003
0,0003 -
7,42503 0,00012
0,00012 -
31,73856;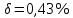
-
48,1026;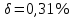
-
3,85508 0,00077
0,00077 -
37,63457;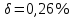
-
30,0039 0,0009
0,0009 -
12,35456;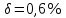
-
75,7242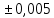
-
13,00466;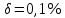
-
5,10459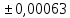
Задание №3.Определить, какое равенство точнее.
Варианты заданий:
Теоретический материал:
Значащей цифрой приближенного числа - называется всякая цифра в его десятичном изображении, отличная от нуля, и нуль, если он содержится между значащими цифрами или является представителем сохраненного десятичного разряда. Все остальные нули, входящие в состав приближенного числа и служащие лишь для обозначения десятичных разрядов его, не причисляются к значащим цифрам.
Значащая цифра называется верной в широком смысле если абсолютная погрешность числа не превосходит одной единицы разряда, соответствующего этой цифре.
Значащая цифра называется верной в узком смысле если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.
В противном случае цифра считается сомнительной.
Краткие сведения, необходимые для работы в MATLAB:
MATLAB - это популярная система компьютерной математики, которая предназначена для выполнения инженерных и научных вычислений.
После запуска MATLAB на экране появляется основное окно приложения.(см. рисунок 1) Это окно содержит меню, панель инструментов и рабочую область - Command Window. Признаком готовности системы к выполнению команды является наличие знака приглашения », после которого расположен активный курсор. Рабочую область со знаком приглашения обычно называют командной строкой. Ввод команд в MATLAB осуществляется с клавиатуры. Нажатие клавиши Enter заставляет систему выполнить команду и вывести результат.
Клавиши «Стрелка вверх» ↑ и «Стрелка вниз» ↓ управляют курсором, однако в MATLAB они имеют другое назначение. Эти клавиши позволяют вернуть в командную строку ранее введенные команды или другую входную информацию, так как вся эта информация сохраняется в специальной области памяти. Так, если в пустой активной командной строке нажать клавишу ↑, то появится последняя вводимая команда, повторное нажатие вызовет предпоследнюю и так далее. Клавиша ↓ выводит команды в обратном порядке.
Зона редактирования - это фактически командная строка. В ней действуют элементарные приемы редактирования:
→ - перемещение курсора вправо на один символ;
← - перемещение курсора влево на одни символ;
Ноmе - перемещение курсора в начало строки;
End - перемещение курсора в конец строки;
Del - удаление символа после курсора;
Backspace - удаление символа перед курсором.
К
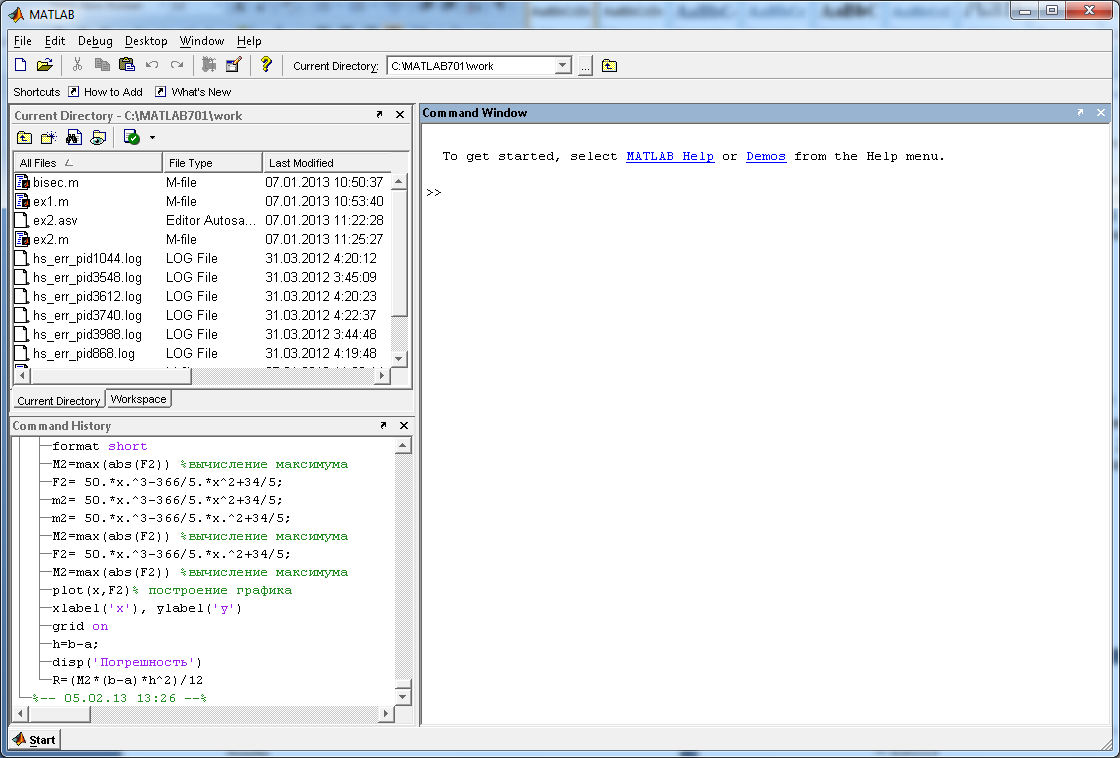 роме того, существуют особенности ввода команд. Если команда заканчивается точкой с запятой «;», то результат ее действия не отображается в командной строке. В противном случае, при отсутствии знака «;», результат действия команды сразу же выводится в рабочую область.
роме того, существуют особенности ввода команд. Если команда заканчивается точкой с запятой «;», то результат ее действия не отображается в командной строке. В противном случае, при отсутствии знака «;», результат действия команды сразу же выводится в рабочую область.Рисунок 1. Основное окно приложения MatLab
Пример №1.
Задание: Определить, какое равенство точнее.
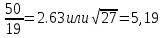
Решение:
Сравним границы относительных погрешностей (предельно относительных погрешностей)
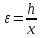 , определив границы абсолютных погрешностей
, определив границы абсолютных погрешностей 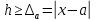 . Для этого вычислим значения исходных равенств с большим числом знаков после запятой:
. Для этого вычислим значения исходных равенств с большим числом знаков после запятой: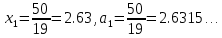
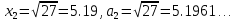
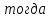
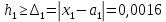
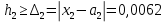
В свою очередь
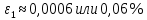
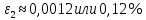
Так как 0,06% > 0,12%, то равенство
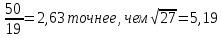
Вычисления в MatLab:
>> a1=50/19
a1 =
2.6316
>> x1=2.63
x1 =
2.6300
>> a2=sqrt(27)
a2 =
5.1962
>> x2=5.19
x2 =
5.1900
>> h1=abs(x1-a1)
h1 =
0.0016
>> h2=abs(x2-a2)
h2 =
0.0062
>> e1=h1/a1*100
e1 =
0.0600
>> e2=h2/a2*100
e2 =
0.1184
Пример №2.
Задание: Округлить сомнительные числа, оставив верные знаки в узком смысле. Определить абсолютную погрешность результата.
1,784;
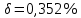
Решение:
Используем определение:
Цифра называется верной в узком смысле, если абсолютная погрешность не превосходит половины единицы десятичного разряда, выраженного этой цифрой.
Найдем абсолютную погрешность исходного числа
h=(0.352%*1.784)/100%=0.0063 (более точное вычисления не требуется, т.к. нас интересует, превосходит ли эта погрешность половину единицы десятичного разряда или нет).
0,0063 > 0,0005
 4 – сомнительная цифра в узком смысле.
4 – сомнительная цифра в узком смысле.0,0063 > 0,005
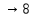 – сомнительная цифра в узком смысле.
– сомнительная цифра в узком смысле.0,0063< 0,05
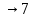 – верная цифра в узком смысле, занимает разряд десятичных долей, т.е. округляем до десятых:
– верная цифра в узком смысле, занимает разряд десятичных долей, т.е. округляем до десятых:1,784
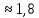
Проверим, все ли цифры получившегося числа являются верными. Для этого вычислим погрешность результата:
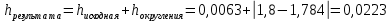
0,0223<0.05
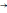 в числе 1,8 цифра 8 а, следовательно, и все предыдущие верны в узком смысле. Итак, ответ 1,8
в числе 1,8 цифра 8 а, следовательно, и все предыдущие верны в узком смысле. Итак, ответ 1,8 0,0223
0,0223Пример №3.
Задание: Округлить сомнительные цифры числа, оставив верные знаки в широком смысле. Определить абсолютную погрешность результата.
0,85637;
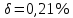
Решение:
Используем определение:
Цифра называется верной в широком смысле, если абсолютная погрешность этого числа не превосходит единицы десятичного разряда, выраженного этой цифрой.
Вычислим абсолютную погрешность исходного числа:
H=(0,85637*0,21%)/100%=0,0018
0,0018 > 0.00001 -7- сомнительная цифра в широком смысле;
0,0018 > 0.0001 -3- сомнительная цифра в широком смысле;
0,0018 > 0.001 -6- сомнительная цифра в широком смысле;
0,0018 < 0.01 -5- верная цифра в широком смысле;
Таким образом, округлим исходное число до верных в широком смысле цифр:
0,85637
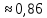
Проверим верность цифр округленного числа. Для этого вычислим погрешность результата
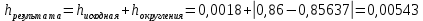
0,00543<0.01 – e у числа 0,86 все цифры верные в широком смысле.
Содержание отчета:
1. Титульный лист.
2. Цель лабораторной работы.
3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.
4. Расчетная часть: описание выполнения задания в среде MatLab.
5. Выводы и анализ полученных результатов.
Контрольные вопросы:
-
Дайте определение приближенного числа -
Сформулируйте правила округления чисел. -
Как находится абсолютная погрешность приближенного числа. -
Как находится относительная погрешность приближенного числа. -
Верной цифрой в узком смысле называется ….. -
Верной цифрой в широком смысле называется ….. -
Как в среде MatLab записать элементарные математические функции:-
Синус числа Х -
Косинус числа Х -
Тангенс числа Х -
Котангенс числа Х -
Корень квадратный из числа Х -
Модуль числа Х -
Экспонента числа Х -
Натуральный логарифм числа Х
-
Лабораторная работа №2.
«Основы теории погрешностей»
Цель: Научиться производить действия над приближенными величинами, вычислять погрешности результатов.
Задание №1. Вычислить и определить погрешности результата. Вычисления выполнить в MatLab.
Варианты заданий:
-
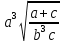 где a=72.79(
где a=72.79(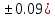 b=3.05(
b=3.05(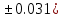 c=55.9(
c=55.9(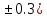
-
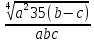 где a=3.09(
где a=3.09(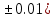 b=41.089(
b=41.089(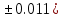 c=0.999(
c=0.999(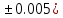
-
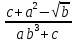 где a=13.5(
где a=13.5(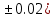 b=3.7(
b=3.7(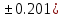 c=4.22(
c=4.22(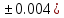
-
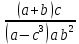 где a=34.5(
где a=34.5(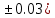 b=23.725(
b=23.725(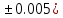
-
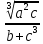 где a=3.09(
где a=3.09(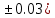 b=11.077(
b=11.077(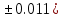 c=5.205(
c=5.205(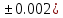
-
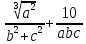 где a=10.007(
где a=10.007(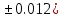 b=1.3577(
b=1.3577(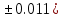 c=5.205(
c=5.205(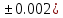
-
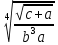 где a=35.309(
где a=35.309(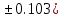 b=6.0207(
b=6.0207(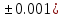 c=52.7044(
c=52.7044(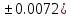
-
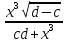 где x=13.254(
где x=13.254(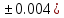 c=77.0348(
c=77.0348(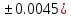 d=90.205(
d=90.205(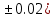
-
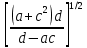 где a=0.011(
где a=0.011(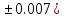 c=2.139(
c=2.139(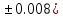 d=44.112(
d=44.112(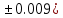
-
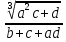 где a=3.091(
где a=3.091(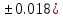 b=22.044(
b=22.044(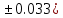 c=9.137(
c=9.137(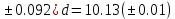
-
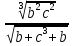 где b=104.023(
где b=104.023(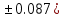 c=23.4567(
c=23.4567(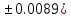
-
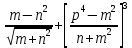 где m=32.14(
где m=32.14(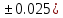 n=1.74(
n=1.74(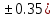 p=29.005(
p=29.005(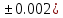
-
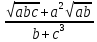 где a=65.034(
где a=65.034(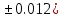 b=4.03(
b=4.03(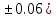 c=30.089(
c=30.089(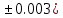
-
c=18.5(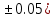
-
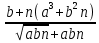 где a=27.309(
где a=27.309(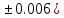 b=42.8(
b=42.8(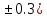 c=5.2(
c=5.2(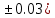
-
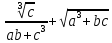 где a=5.79(
где a=5.79(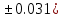 b=11.45(
b=11.45(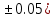 c=2.05(
c=2.05(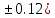
Задание №2: Выясните погрешность задания исходных данных, необходимую для получения результата с m=5 верными значащими цифрами. Вычисления провести в среде MatLab.
Варианты заданий:
-
 где a = 5.79 b = 11.45 c =2.05
где a = 5.79 b = 11.45 c =2.05 -
 где a=27.309 b=42.8 c=5.2
где a=27.309 b=42.8 c=5.2 -
 где a=34.5 b=23.725 c=18.5
где a=34.5 b=23.725 c=18.5 -
 где a = 13.5 b = 3.7 c = 4 .22
где a = 13.5 b = 3.7 c = 4 .22 -
 где a=3.09 b=41.089 c=0.999
где a=3.09 b=41.089 c=0.999 -
 где a=72.79 b=3.05 c=55.9
где a=72.79 b=3.05 c=55.9 -
 где a=65.034 b=4.03 c=30.089
где a=65.034 b=4.03 c=30.089 -
 где m=32.14 n=1.74 p=29.005
где m=32.14 n=1.74 p=29.005 -
 где b=104.023 c=23.4567
где b=104.023 c=23.4567 -
 где a=3.091 b=22.044 c=9.137
где a=3.091 b=22.044 c=9.137 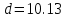
-
 где a=0.011 c=2.139 d=44.112
где a=0.011 c=2.139 d=44.112 -
 где x=13.254 c = 77.0348 d=90.205
где x=13.254 c = 77.0348 d=90.205 -
 где a=35.309 b=6.0207 c=52.7044
где a=35.309 b=6.0207 c=52.7044 -
 где a=10.007 b=1.3577 c=5.205
где a=10.007 b=1.3577 c=5.205 -
 где a = 3.09 b = 11.077 c = 5.205
где a = 3.09 b = 11.077 c = 5.205
Пример:
Задание
x=
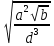 +
+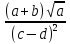
где a=2.754(
 b=11.7(
b=11.7(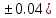 c=10.536(
c=10.536(
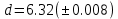
Решение
Имеем:
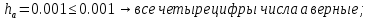
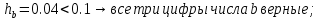
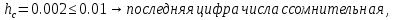
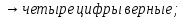
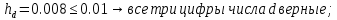
Вычислим приближенное значение выражения, применяя правила;
-
При сложении и вычитании сохраняем столько десятичных знаков, сколько их в приближенном исходном данном с наименьшим числом верных десятичных знаков + один «запасной» -
При умножении и делении сохраняем столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр + одна «запасная» -
При возведении в степень и при извлечении корня в результате сохраняем столько значащих цифр, сколько верных значащих цифр имеет исходное число + один знак. -
Итоговый результат округлим до трёх значащих цифр.
Первое слагаемое
 =0,32
=0,32Второе слагаемое
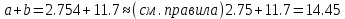
 =1,349
=1,349X=1.6696
 1.67
1.67Оценим погрешность результата если
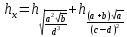
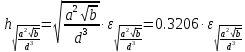
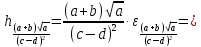 1.349
1.349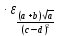
Оценим относительную погрешность первого слагаемого
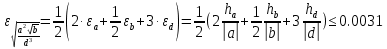
Тогда оценка абсолютной погрешности первого слагаемого
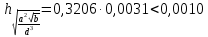 возьмем
возьмем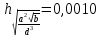
Оценим относительную погрешность вычисления второго слагаемого
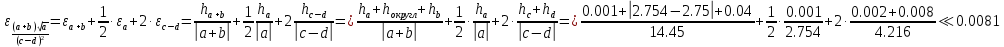
Тогда
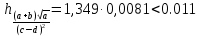 возьмем
возьмем 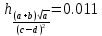
Таким образом
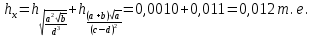
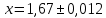
Отсюда следует, что верными являются только две цифры (0.01<0.012<0.1)
Округлим результат до верных знаков : х=1,67
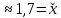 с учетом этого погрешность измениться:
с учетом этого погрешность измениться: 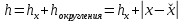 =0.012+
=0.012+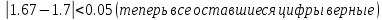
Качество вычисления составляет 100%-
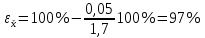
Итак, окончательный ответ 1,7
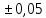
Содержание отчета:
1. Титульный лист.
2. Цель лабораторной работы.
3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.
4. Расчетная часть: описание выполнения задания в среде MatLab.
5. Выводы и анализ полученных результатов.
Контрольные вопросы:
-
Как находится абсолютная погрешность приближенного числа. -
Как находится относительная погрешность приближенного числа. -
Чему равна погрешность суммы 2-х приближенных чисел? -
Чему равна погрешность разности 2-х приближенных чисел? -
Сформулируйте правило вычисления погрешности произведения 2-х приближенных чисел. -
Сформулируйте правило вычисления погрешности частного 2-х приближенных чисел.