Файл: Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11.docx

Задание 2:
Решить задания с помощью:

1. 
   метода Гаусса
   
2. 
   LU-разложения
   

Варианты заданий:

	0,24 x2– 0,08 x3 = 8; 0,09 x1 +3 x2 – 0,15 x3 = 9; 0,04 x1 – 0,08 x2 + 4 x3 = 20.
	10 x1 +2 x2 + x3 = 35; x1 + 5 x2 = 29; 2 x1 + 0,5 x2 + 4x3 = 34.
	4 x1 + x2 + x3= 24; 5x1 + 3 x2 + 2 x3 = – 10; 2 x1 + x2+ 7 x3 = -28.
	7 x1 + 5 x2 + 2 x3 = 48; 2 x1 + 10 x2 = 27; x1 + 2x2 – 3 x3 = 18.
	10x1 + 2 x2 + x3 = 32; 7x1 + 5 x2 + x3 = 47; 2 x1 + 0,5 x2 + 4 x3= 30.
	2,45x1+1,75x2-3,24x3=1,23 1,75x1-1,16x2+2,18x3=3,43 -3,24x1+2,18x2-1,85x3= 0,16
	0,21x1-0,94x3=-0,25 0,98x1-0,19x2+0,93x3=0,23 0,87x1+0,56x2=0,33
	2 x1 + x3 = -3; 3 x1 + 5 x2 – 2 x3 = 1; x1– 4 x2 + 10 x3 = 0.
	5 x1 + x2 + 2 x3 = 17; 2 x1 – x3 = -7; x1 – 2 x2 + 8 x3 = 36.
	5 x1 + 2 x2+ x3 = 19; x1 + 4 x2 + 2 x3= 11; 2 x1 + 0,4 x2 + 6 x3 = 21.
	2x1 + 0,5 x2 + 0,5 x3 = 12; x1 + 3 x2 + x3 = -4; 3 x1– 8 x3 = 68.
	4 x1 – x2 –2 x3= 15; 3 x1 + 6x2 – x3 = 19; x1 + 0,7x2 + 3 x3 = 13.
	5,4x1-2,46x2+3,9 x3=5,51 2,57x1+6,28x2-1,3x3=4,45 2,71x1+1,59x3=-3,57
	3,43x1+4,07x2=46,08 74,4x1+1,8x2-1,8x3=-21,5 94,3x2+1,02x3=92,3

Пример решения СЛАУ в MatLab :

Дана система уравнений:


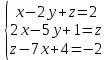
Решение системы x=A^-1b

---

A=[1 -2 1; 2 -5 -1; -7 0 1];

b=[2; -1; -2];

x=inv(A)*b

Результатом будет:

x =

0.5200

0.0800

1.6400
Метод Крамера:

% Решим систему методом Крамера
A = [1 2 3 4; -1 2 -3 4; 0 1 -1 1; 1 1 1 1];
b = [30;10;3;10];

% Проверим невырожденность системы
rank(A)

>>  ans = 4

% По правилу Крамера
A1 = A;
A2 = A;
A3 = A;
A4 = A;
A1(:,1) = b;
A2(:,2) = b;
A3(:,3) = b;
A4(:,4) = b; 

x1 = det(A1) / det(A);
x2 = det(A2) / det(A);
x3 = det(A3) / det(A);
x4 = det(A4) / det(A);
x=[x1;x2;x3;x4]

% Проверим решение
A*x - b

>>	ans =	0
		0
		0
		0

Метод Гаусса:

Решение системы линейных уравнений при помощи метода Гаусса основывается на том, что от заданной системы, переходят к системе эквивалентной, которая решается проще, чем исходная.

Метод Гаусса состоит из двух этапов:

• 
  Первый этап - это прямой ход, в результате которого расширенная матрица системы путем элементарных преобразований (перестановка уравнений системы, умножение уравнений на число, отличное от нуля, и сложение уравнений) приводится к ступенчатому виду.
  
• 
  На втором этапе (обратный ход) ступенчатую матрицу преобразуют так, бы в первых n столбцах получилась единичная матрица. Последний, n +1 столбец этой матрицы содержит решение системы линейных уравнений.
  

Порядок решения задачи в MATLAB следующий:

• 
  сформировать матрицу коэффициентов Aи вектор свободных членов b заданной системы;
  
• 
  сформировать расширенную матрицу системы, объединив A и b;
  
• 
  используя функцию rref, привести расширенную матрицу к ступенчатому виду;
  
• 
  найти решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте;
  
• 
  выполнить вычисление Ax-b; если в результате получился нулевой вектор, задача решена верно.
  

A=[1 -2 1; 2 -5 -1; -7 0 1];

b=[2; -1; -2];

C=rref([A b]); %Приведение расширенной матрицы к треугольному виду

---

x=C(1:3,4:4)%Выделение последнего столбца из матрицы

Результатом будет:

x =

0.5200

0.0800

1.6400
Метод LU – разложения:

Рассмотрим пример решения системы



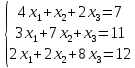
с предварительным LU-разложением матрицы.

A = [4 1 2; 3 7 1 ; 2 2 8];

f = [7; 11; 12];

Выполняем LU-разложение

[L, U] = lu(A);

и решаем последовательно две системы с треугольными матрицами, сначала с L, затем с U

y = L\f;

x = U\y
x =

1

1

1

Решение двух систем можно записать одним выражением

x = U\(L\f)

и результат получится тем же самым. Следует обратить внимание на важность использования скобок для определения порядка решения систем с треугольными матрицами.
Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.
Контрольные вопросы:

1. 
   Какая функция называется аналитической?
   
2. 
   В чем заключается решение систем уравнений методом Крамера?
   
3. 
   Для каких матриц существуют обратные матрицы?
   
4. 
   В каких случаях нельзя пользоваться формулами Крамера?
   
5. 
   Суть метода Гаусса.
   
6. 
   В каких случаях возможно решение систем уравнений методом Крамера?
   
7. 
   С помощью какой функции в Матлаб можно вычислить определитель матрицы?
   
8. 
   С помощью какой функции в Матлаб можно ввести матрицу?
   
9. 
   Что значит решить СЛАУ?
   
10. 
    Какие методы решения СЛАУ Вы знаете?
    

---

Лабораторная работа №6.

«Метод прогонки для трехдиагональных систем»

Цель: научиться вычислять корни систем линейных алгебраических уравнений различными методами.
Задание:Решить систему линейных алгебраических уравнений с помощью метода прогонки. И определить невязку и сделать анализ точности вычислений.

Варианты заданий:

№ варианта	Матрица системы				Правая часть
1	0.401 -0.029 0.000 0.000	0.301 -0.500 -0.050 0.000	0.000 -0.018 -1.400 -0.007	0.000 0.000 -0.039 -2.300	0.122 -0.253 -0.988 -2.082
2	-1.700 0.002 0.000 0.000	0.003 0.800 -0.002 0.000	0.000 0.001 -0.100 -0.003	0.000 0.000 0.030 -1.600	0.681 0.480 -0.802 -1.007
3	-3.000 -0.011 0.000 0.000	0.001 2.100 0.005 0.000	0.000 0.5200 1.200 -0.010	0.000 0.000 0.600 -0.300	1.514 1.478 1.083 -1.007
4	4.300 0.100 0.000 0.000	0.217 -3.400 0.090 0.000	0.000 -0.207 2.500 0.080	0.000 0.000 0.197 -1.600	2.663 2.778 2.533 1.928
5	-5.600 0.147 0.000 0.000	0.268 4.700 -0.150 0.000	0.000 0.271 -3.800 0.153	0.000 0.000 0.274 2.900	4.032 4.313 4.235 3.797
6	6.900 0.191 0.000 0.000	0.319 -6.000 -0.205 0.000	0.000 -4.040 5.100 0.020	0.000 0.000 0.000 4.200	5.664 6.112 6.201 5.937
№ варианта	Матрица системы				Правая часть
7	-8.200 0.234 0.000 0.000	0.370 7.300 0.260 0.000	0.000 5.600 -0.340 0.268	0.000 0.000 -0.422 5.500	7.559 8.175 8.421 8.322
8	9.500 0.278 0.000 0.000	0.422 8.601 0.315 0.000	0.000 0.459 7.700 0.351	0.000 0.000 0.496 6.803	9.719 10.500 10.915 10.978
9	10.800 0.321 0.000 0.000	-0.5760 9.900 0.369 0.000	0.000 7.300 9.000 0.416	0.000 0.000 -6.060 8.100	12.143 13.089 13.674 13.897
10	-1.100 0.365 0.000 0.000	0.528 0.113 -0.423 0.000	0.000 0.536 1.031 0.481	0.000 0.000 0.534 -0.570	14.830 15.941 16.969 17.081
11	13.400 -0.408 0.000 0.000	0.581 12.500 0.477 0.000	0.000 -0.650 -11.600 0.546	0.000 0.000 0.781 10.700	17.782 19.593 19.974 20.528
12	30.300 0.975 0.000 0.000	0.153 -29.400 0.117 0.000	0.000 0.011 -2.500 10.700	0.000 0.000 1.660 27.600	80.168 83.578 86.609 89.278
13	0.161 0.109 0.000 0.000	0.332 -0.301 -0.060 0.000	0.000 -0.150 0.171 0.145	0.000 0.000 0.051 -0.298	86.814 90.358 19.861 93.502
14	-22.500 0.714 0.000 0.000	-0.956 21.600 0.855 0.000	0.000 0.109 20.714 -0.996	0.000 0.000 0.124 19.800	45.802 48.261 50.343 52.453

---

№ варианта	Матрица системы				Правая часть
15	26.400 0.840 0.000 0.000	0.117 -25.513 0.105 0.000	0.000 0.198 24.600 0.000	0.000 0.000 -8.810 2.451	61.853 64.730 63.880 59.376

Теоретический материал:

Метод прогонки является одним из эффективных методов решения СЛАУ с трех - диагональными матрицами, возникающих при конечно-разностной аппроксимации задач для обыкновенных дифференциальных уравнений (ОДУ) и уравнений в частных производных второго порядка и является частным случаем метода Гаусса. Рассмотрим следующую СЛАУ:

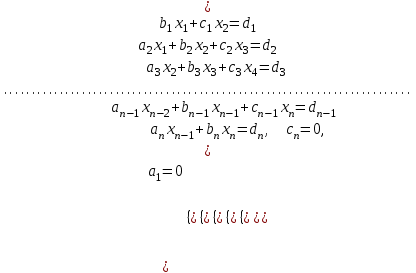решение, которое будем искать в виде: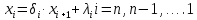



Где 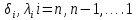- прогоночные коэффициенты, подлежащие определению.

, ;
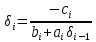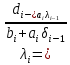Пример решения СЛАУ методом прогонки в MatLab :


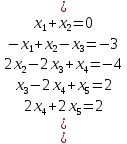
Решение:

Найти коэффициенты прогонки

,

1. 
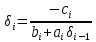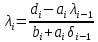
   Прямая прогонка
   

A=[1,1,0,0,0;-1,1,-1,0,0;0,2,-2,1,0;0,0,1,-2,1;0,0,0,2,2]

A =

1 1 0 0 0

-1 1 -1 0 0

0 2 -2 1 0

0 0 1 -2 1

0 0 0 2 2

>> B=[0;-3;-4;2;2]

B =

0

-3

-4

2

2

>> %обозначим коэффициенты прогонки δ=d, λ=n

>> d1=-A(1,2)/A(1,1)

d1 = -1

>> n1=B(1,1)/A(1,1)

n1 = 0

>>d2=-A(2,3)/(A(2,2)+A(2,1)*d1)

d2 = 0.5000

>> n2=(B(2,1)-A(2,1)*n1)/(A(2,2)+A(2,1)*d1)

n2 = -1.5000

>> d3=-A(3,4)/(A(3,3)+A(3,2)*d2)

d3 = 1

>> n3=(B(3,1)-A(3,2)*n2)/(A(3,3)+A(3,2)*d2)

n3 = 1

>> d4=-A(4,5)/(A(4,4)+A(4,3)*d3)

d4 = 1

>> n4=(B(4,1)-A(4,3)*n3)/(A(4,4)+A(4,3)*d3)

n4 = -1

>> n5=(B(5,1)-A(5,4)*n4)/(A(5,5)+A(5,4)*d4)

n5 = 1

2. 
   Получаем обратную прогонку
   

---