Файл: Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11.docx

>> plot(x1,y1,'-k',x,y,'ok')

13. 
    Из графика (см. Рисунок 7) можно сделать вывод, что полином вида Y=ax³+bx²+cх+d является аппроксимурующей кривой для исходных данных
    

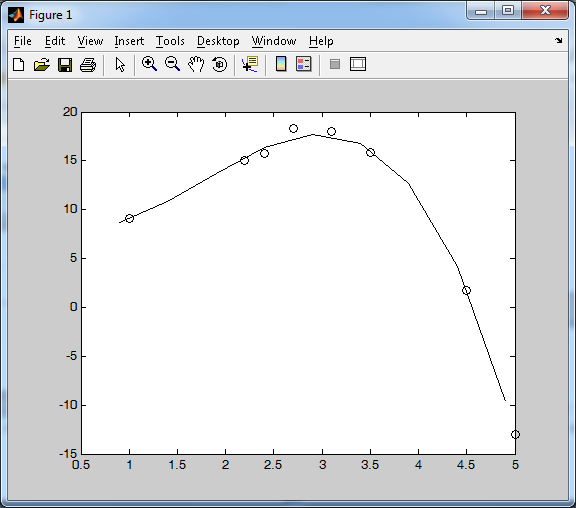
Рисунок 7. График функции
Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   В каком случае возникает необходимость постановки задачи аппроксимации?
   
2. 
   Сформулируйте задачу аппроксимации функции?
   
3. 
   Какая кривая называется линией регрессии?
   
4. 
   В чем заключается задача аппроксимации?
   
5. 
   Для чего используется аппроксимация функции на практике?
   
6. 
   В каком виде Вы искали линию регрессии?
   
7. 
   Для чего используется метод наименьших квадратов?
   
8. 
   Что называется аппроксимирующей кривой?
   

---

Лабораторная работа 13.

«Численное дифференцирование функции. Методы дифференцирования»

Цель: научиться применять интерполяционные формулы численного дифференцирования для нахождения первой и второй производной функции в точках.
Задание: Найти значения производных y’ и y’’ в точках x_i. Выполнить эту задачу также в системе MatLab.
Варианты заданий:

№	xi	1	2	3	4	5	6	х
1	yi	0,7	1,9	1,1	2,2	3,5	4,1	1; 3; 5;
2	yi	0,8	2,4	1,5	2,3	4,0	4,7	2; 4; 5;
3	yi	2,1	3,0	1,5	3,2	4,1	5,3	1; 4; 6;

№	xi	0,0	0,2	0,4	0,6	0,8	1	х
4	yi	1,000	1,221	1,491	1,822	2,225	2,742	0,0 0,4 0,8
5	yi	1,002	1,210	1,500	1,842	2,236	2,812	0,2; 0,6; 0,8;
6	yi	1,003	1,230	1,495	1,853	2,257	2,356	0,0;0,4;1,0;
№	xi	-0,4	-0,2	0,0	0,2	0,4	0,6	х
7	yi	0,67	0,82	1,00	1,22	1,49	1,82	-0,4 0,0; 0,4;
8	yi	0,78	0,95	1,23	1,51	1,78	2,00	-0,2 0,2; 0,6
9	yi	0,84	1,07	1,31	1,59	1,87	2,14	-0,4 0,2; 0,4
10	yi	0,53	0,72	1,04	1,42	1,64	1,93	-0,2 0,0; 0,6

---

№	xi	0,5	0,6	0,7	0,8	0,9	1,0	х
11	yi	0,479	0,564	0,644	0,7174	0,7833	0,841	0,5; 0,7; 1,0
12	yi	0,944	0,645	0,326	0,4717	0,3387	0,5184	0,6; 0,8; 0,9
13	yi	0.534	0.645	0.256	0.6235	0.5126	0.158	0.1; 0,3; 0,6
14	yi	0.456	0.542	0.632	0.3256	0.2365	0.125	0,2; 0,4; 0,6
15	yi	0,78	0,95	1,23	1,51	1,78	2,00	-0,2 0,2; 0,6

Теоретический материал:

Для определения производной функции представленной виде таблицы используются формулы приближенного дифференцирования.

1. 
   Формулы приближенного дифференцирования, основанные на формулах Ньютона
   

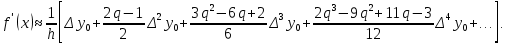
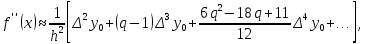
Что бы получить значение производной в точке, лежащей в конце таблицы, пользуются второй интерполяционной формулой Ньютона.

2. 
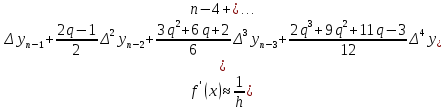
   Формулы приближенного дифференцирования, основанные на формуле Лагранжа
   

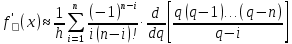
Произведем расчет для n=4, функция f(x) задана 5 табличными значениями. Имеем:

---

n = 4 (пять точек).











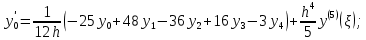
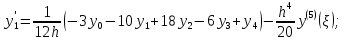
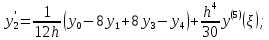
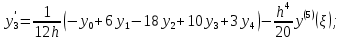
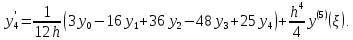
Где - точка отрезка [a, b], отличная от узлов интерполяции.

Как известно, численное дифференцирование строится на использовании аппарата конечных разностей и соответствующего многообразия аппроксимаций. Здесь полезны функции:

diff(X), diff(X, n), diff(X, n, dim) - вычисление конечных разностей (первых, n-го порядка или по указанному измерению); если Х -массив, берутся разности между столбцами:

>> F= [ 0 0.0998 0.1987 0.2955 0.3894 0.4794]

>> D=diff(F)

D = 0.0998 0.0988 0.0969 0.0939 0.0900

>> D2=diff(F,2)

D2 = -0.0010 -0.0020 -0.0030 -0.0039
Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.
Контрольные вопросы:

1. 
   Сформулируйте задачу численного дифференцирования?
   
2. 
   Запишите первую формулу Ньютона для нахождения первой производной.
   
3. 
   Запишите вторую формулу Ньютона для нахождения второй производной.
   
4. 
   Запишите формулу Логранжа для нахождения первой производной.
   
5. 
   Основные методы дифференцирования.
   
6. 
   Какой метод численного дифференцирования Вы выбрали? Почему?
   
7. 
   Численное дифференцирование для равностоящих точек, выраженные через значения функции в этих точках (формула?).
   
8. 
   Чему равна погрешность производной интерполирующей функции?
   
9. 
   Какая команда в матлабе возвращает конечные разности порядка n.
   

---

Лабораторная работа №14.

« Численное интегрирование функции»

Цель работы: научиться выполнять численное интегрирование заданной функции.
Задание:

1. 
   Выполнить численное интегрирование заданной функции f(x) в заданных пределах a, b. в системе MatLab.
   

Использовать методы:

1. 
   Метод прямоугольников
   
2. 
   Метод трапеций
   
3. 
   Метод Симпсона
   
4. 
   Метод Ньютона – Котеса
   

2. 
   Оценить погрешности квадратурных формул правилом Рунге.
   

Варианты заданий:

Вариант	f(x)	a	b
1	(4x – x2)	0	2
2	4/(1 + x2)	0	1
3	sin x/ x	0	1
4	(1 – x2)0,5	-1	1
5	sin2x/(1 + x5)	0	3
6	sin4x exp(-2x)	0	1
7	1/x0,5	0.04	2
8	1/(x2 + 0,1)	0	2
9	sin(1/x)	1/2p	1
10	exp(x2/2)	0	1
11		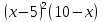0	1
12	(x – x2)	1	3
13	sin x/(1 + x5)	0	2
14		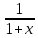0	2

Методы численного интегрирования

К вычислениям определенных интегралов сводятся многие практические задачи физики, химии, экологии, механики и других естественных наук. На практике взять интеграл аналитически не всегда удается. В этом случае используются методы численного интегрирования. В данной лабораторной работе рассматриваются методы Ньютона - Котеса, в частности методы прямоугольников, трапеций, Симпсона и метод Гаусса. Кроме того, в лабораторной работе рассматриваются способы аналитического и численного отыскания интегралов средствами MATLAB.

---