Файл: Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 253
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
«Решение нелинейных уравнений»
«Решение систем линейных алгебраических уравнений»
«Метод прогонки для трехдиагональных систем»
« Использование итерационных численных методов для решения СЛАУ»
« Использование итерационных численных методов для решения СЛАУ»
«Численное решение алгебраических проблем собственных значений»
«Интерполирование. Интерполяционные формулы»
Интерполяционная схема Эйткена
« Интерполирование. Интерполяционные формулы»
«Аппроксимация, построение аппроксимирующих кривых»
«Численное дифференцирование функции. Методы дифференцирования»
Теоретический материал:
Формула Лагранжа:
Наиболее общей формулой параболического интерполирования является интерполяционная формула Лагранжа.
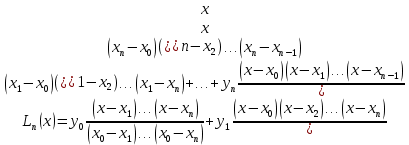
Интерполяционная схема Эйткена
Применение формулы Лагранжа для вычисления интерполяционного многочлена в точке неудобно из-за ее громоздкости. Существенно упростить расчет интерполяционного многочлена в конкретной точке можно, используя интерполяционную схему Эйткена, которая заключается в следующем.
На первом этапе строится последовательность многочленов первой степени по двум рядом стоящим узлам:
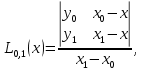
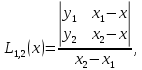
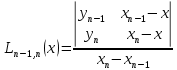
Очевидно, что все построенные многочлены являются многочленами Лагранжа (здесь
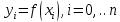 ) На втором этапе строится последовательность многочленов Лагранжа 2-й степени, при этом используются многочлены, вычисленные на предыдущем этапе. Расчеты выполняются по формулам
) На втором этапе строится последовательность многочленов Лагранжа 2-й степени, при этом используются многочлены, вычисленные на предыдущем этапе. Расчеты выполняются по формулам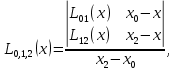
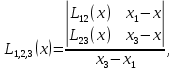
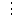
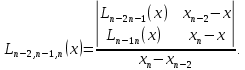
Количество таких многочленов будет на 1 меньше, чем на предыдущем этапе. Наконец на n-м этапе строится многочлен Лагранжа степени n по формуле
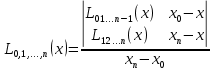
Это и будет значение многочлена Лагранжа степени n в точке x , построенного по узлам
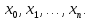
Пример построения интерполяционного многочлена Лагранжа в среде MatLab7.0 по таблице:
| x | -1 | 0 | 1 | 2 | X |
| y | 4 | 2 | 0 | 1 | 1.5 |
1.Введем данные:
>> x = [-1 0 1 2]
>> y = [4 2 0 1]
2.Построим интерполяционный многочлен (аппроксимация третьей степени):
>> p = polyfit(x, y, 3)
Коэффициенты интерполяции
p = 0.5000 0.0000 -2.5000 2.0000
Многочлен Лагранжа
L=0.5*x.^3-2.5*x+2
3.Построим график функции и узлы интерполяции (см. Рисунок 4). Для графика зададим больше значений, чем в исходной таблице
>> x1=[-1:0.1:2];
>> L=0.5*x1.^3-2.5*x1+2 ;
>> plot(x1, L, 'r', x, y, '*')
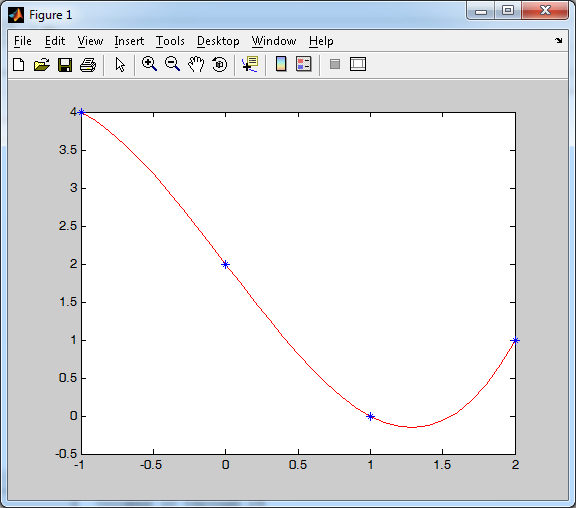
Рисунок 4. График функции
Содержание отчета:
-
Титульный лист. -
Цель лабораторной работы. -
Исходные данные, указываемые в задании и необходимые для достижения поставленной цели. -
Расчетная часть: описание выполнения задания -
Проверка результатов в среде MatLab. -
Выводы и анализ полученных результатов.
Контрольные вопросы:
-
Постановка задачи теории интерполирования; -
Интерполяционный многочлен Лагранжа; -
Остаточный член интерполяционной формулы Лагранжа и его оценка; -
Вычислительная схема Эйткена; -
Какими командами реализуется построение графиков в среде MatLab; -
Что означает запись: 0.5*x.^3 в среде MatLab;
Лабораторная работа №11.
« Интерполирование. Интерполяционные формулы»
Цель: научиться применять интерполяционные формулы для заданной совокупности данных.
Задание:
1. Подобрать интерполяционный полином по формулам Ньютона для следующей совокупности данных xi, yi., найти значение полинома в точках z1 и z2, найти погрешность.
2. Вычислить значения функции в точках z3 и z4, используя сплайн-интерполяцию.
3. Найти значения функции в точках z1, z2, z3, z4 используя среду MatLab.
Варианты заданий:
| Вариант | xi | 1 | 2 | 3 | 4 | 5 | z1 | z2 | z3 | z4 |
| | yi | 0,7 | 1,9 | 1,1 | 2,2 | 3,5 | 2,2 | 4,8 | 2,1 | 1,1 |
| | yi | 0,8 | 2,4 | 1,5 | 2,3 | 4,0 | 1,2 | 4,6 | 4,6 | 1,1 |
| | yi | 2,1 | 3,0 | 1,5 | 3,2 | 4,1 | 1,8 | 4,4 | 1,1 | 3,3 |
| | yi | 2,2 | 4,8 | 1,9 | 3,9 | 5,5 | 2,2 | 4,9 | 3,5 | 2,5 |
| | yi | 1,0 | 3,5 | 5,0 | 5,6 | 3,8 | 1,1 | 4,8 | 2,1 | 4,8 |
| | yi | 2,6 | 1,1 | 1,6 | 3,2 | 2,4 | 1,5 | 3,9 | 4,5 | 3,9 |
| | yi | 3,5 | 4,8 | 3,5 | 1,8 | 1,5 | 2,1 | 4,2 | 1,3 | 2,1 |
| | yi | 6,0 | 3,2 | 1,9 | 1,3 | 1,2 | 1,9 | 4,1 | 4,9 | 1,9 |
| | yi | 1,5 | 1,8 | 2,5 | 4,0 | 7,0 | 2,2 | 4,8 | 4,8 | 3,6 |
| | yi | 0 | 6,0 | 2,0 | 1,3 | 6,0 | 1,2 | 4,9 | 1,2 | 2,2 |
| | yi | 3,5 | 1,2 | 0 | 1,7 | 2,0 | 1,1 | 3,8 | 3,8 | 4,7 |
| | yi | 1,4 | 2,7 | 6,0 | 0 | 4,8 | 1,9 | 4,9 | 1,9 | 2,3 |
| | yi | 2,1 | 3,1 | 5,1 | 5,8 | 6,0 | 2,1 | 4,8 | 2,1 | 3,3 |
| | yi | 1,3 | 2,4 | 6,0 | 0 | 4,6 | 1,1 | 4,7 | 1,1 | 2,9 |
| | yi | 1,0 | 3,5 | 5,0 | 5,6 | 3,8 | 1,1 | 4,8 | 2,1 | 4,8 |
Теоретический материал:
Вычисление значений функции для значений аргумента, лежащих в начале таблицы, удобно проводить, пользуясь первой интерполяционной формулой Ньютона.
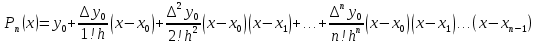
Для интерполирования в конце таблицы обычно применяют вторую интерполяционную формулу Ньютона.
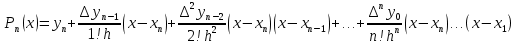
Примеры решения задач интерполяции в MatLab:
1. Интерполяция кубическими сплайнами в среде Matlab осуществляется с помощью функции spline, которая имеет вид:
Yi = spline(x, у, xi).
Здесь:
-
x — вектор узлов интерполяции; -
у — вектор значений функции в узлах интерполяции; -
xi — вектор аргументов функции y(x) из области ее определения, задаваемый пользователем.
Вместо вектора у функция у =f(x) может быть задана в виде формулы.
Функция spline не позволяет получить функцию интерполяции в виде формулы. В этом ее существенный недостаток.
Пусть в результате опыта получены данные:
| | Значение переменных | |||||||
| x | 1 | 4 | 7 | 9 | 13 | 18 | 21 | 27 |
| y | 0.4 | 1.55 | 2.9 | 3.9 | 5.86 | 8.3 | 9.8 | 12.8 |
Необходимо найти значения функции при
x = 3, 6, 10, 14, 20. Процедуры интерполяции будут иметь вид:
x= [1 4 7 9 13 18 21 27];
у= [0.4, 1.55, 2.9, 3.9, 5.86, 8.3, 9.8, 12.8];
xi =[3 6 10 14 20];
Yi = spline(х, у, xi)
После нажатия клавиши <Enter> на экране увидим ответ:
Yi= 1.1458 2.4261 4.3980 6.3444 9.2975
2.Функция interpl наиболее универсальна, она позволяет решать задачи интерполяции несколькими методами.
Функция имеет вид:
Yi = interpl (х, у, xi ,метод).
Здесь:
-
х, у, — векторы узлов и значений функции интерполяции; -
xi — вектор значений аргументов, задаваемый пользователем; -
метод— аргумент, позволяющий пользователю выбрать метод интерполяции.
Методами интерполяции в Matlab являются:
-
‘nearest’— ступенчатая; -
‘linear’ — линейная; -
‘cubic’— кубическая; -
‘spline’ — кубическими сплайнами.
Если метод не указан, то реализуется линейная интерполяция.
Пусть функция у = f(х) задана в виде таблицы значений
| | Значения переменных | ||||||
| x | 2 | 3 | 8 | 12 | 20 | 25 | 36 |
| y | 1 | 2.5 | 4.6 | 6.8 | 5.1 | 3.9 | 3 |
Необходимо определить значения функции при значениях аргументов x= 4, 6, 15, 30.
x=[2,