Файл: Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 11.12.2023

Просмотров: 252

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Лабораторная работа №2.

«Основы теории погрешностей»

Лабораторная работа №3-4.

«Решение нелинейных уравнений»

Лабораторная работа №5.

«Решение систем линейных алгебраических уравнений»

Лабораторная работа №6.

«Метод прогонки для трехдиагональных систем»

Лабораторная работа №7.

« Использование итерационных численных методов для решения СЛАУ»

Лабораторная работа №8.

« Использование итерационных численных методов для решения СЛАУ»

Лабораторная работа №9.

«Численное решение алгебраических проблем собственных значений»

Лабораторная работа №10.

«Интерполирование. Интерполяционные формулы»

Интерполяционная схема Эйткена

Лабораторная работа №11.

« Интерполирование. Интерполяционные формулы»

Лабораторная работа №12.

«Аппроксимация, построение аппроксимирующих кривых»

Лабораторная работа 13.

«Численное дифференцирование функции. Методы дифференцирования»

Лабораторная работа №14.

« Численное интегрирование функции»

Список использованной литературы

Лабораторная работа №3-4.

«Решение нелинейных уравнений»



Цель: Научиться находить корни нелинейных уравнений различными методами.
Задание:

  1. Отделить корни уравнения графическим и аналитическим методом.

  2. Уточнить один из коней с точностью =0,001 методом:

  1. Бисекций;

  2. Простой итерации;

  3. Ньютона;

  4. Хорд;

Решение данного задания должно быть выполнено как в «ручную» так и с использованием среды MatLab.

Варианты заданий:


Уравнение 1
Уравнение 2





  1. 2x-cosx=0.13


  1. x+ sin(x-0.23)=1.41


  1. tg(x+1.7)=2x2


  1. lnx-sinx= -0.2


  1. ln(x+1.1)+2sinx=0


  1. ctgx-x/2=0.41


  1. cosx-2lnx=1.4


  1. ln(2x-3)-tgx=1.2


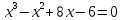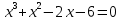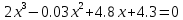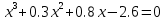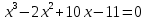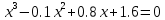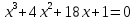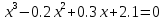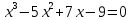Уравнение 1
Уравнение 2

  1. 3x – ex=0.41


  1. 0.4x+sin(x-2.3)=0.47


  1. (2-x)ex=0.3


  1. x2+sin(x+0.23)=0






  1. ln(x+1)-sinx=0


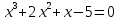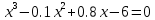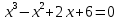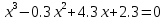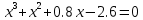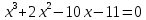Теоретический материал:

Графический метод отделения корней.

  1. Строят график функции y=f(x).

  2. Визуально определяют отрезки, в которых заключено только по одному корню (только одной абсциссе точек пересечения).

  3. Количество действительных корней уравнения y=f(x)определяется числом пересечения графика с осью ОХ.

  4. Если y=f(x) касается ось абсцисс, то уравнение имеет в этой точке двукратный корень

  5. Если y=f(x) имеет перегиб в точке пересечения с осью абсцисс то уравнение имеет в этой точке трехкратный корень

Аналитический метод.

  1. Найти первую производную f`(x)

  2. Составить таблицу знаков функции y=f(x), пологая аргумент х равным:

  • Критическим значениям

  • Граничным значениям

  • Определить интервалы, на концах которых функция принимает значения противоположных знаков. Внутри этих интервалов находится по одному, и только по одному, корню.

    Создание М-файлов в MatLab:

    М-файл- это список команд MATLAB, сохраненный на диске. Для подготовки, редактирования и отладки М-файлов служит специальный редактор, который можно вызвать, выполнив команду главного меню File -> New -> M-file. В результате работы этой команды будет создан новый М-файл. (см. Рисунок 2)

    Рисунок 2. Редактор для создания М-Файлов
    Привести операторы М-файла к выполнению можно несколькими способами:

    • вызвать команду Debug > Run из меню редактора М-файлов;

    • воспользоваться клавиатурой и нажать на кнопку F5;

    • набрать имя М-файла в командной строки и нажать ENTER.

    Текстовый комментарий в MATLAB – это строка, начинающаяся с символа %.
    Построение графиков в MatLab:
    MatLab обладает хорошо развитыми графическими возможностями для визуализации данных.

    Вывод функции одной переменной в виде графика состоит из следующих этапов:

    1. Задание вектора значений аргумента х.
    2. Вычисление вектора у значений функции y(х).

    3. Вызов команды  plot  для построения графика.
    Команды для задания вектора х и вычисления функции лучше завершать точкой с запятой для подавления вывода в командное окно их значений (после команды plot точку с запятой ставить необязательно, т. к. она ничего не выводит в командное окно).

    Пример решения нелинейного уравнения в среде MatLab:

    Уравнение имеет вид : 3x4+8x3+6x2-11=0

    1. Строим график (см. Рисунок 3)

    >> x=[-2:0.1:5]

    >> f= 3*x.^4-8*x.^3-18*x.^2+2

    >> plot(x,f)

    >> grid

    1. Функция имеет 4 точки пересечения с осью ОХ.

    -1

    -0,5

    0,5

     4,1



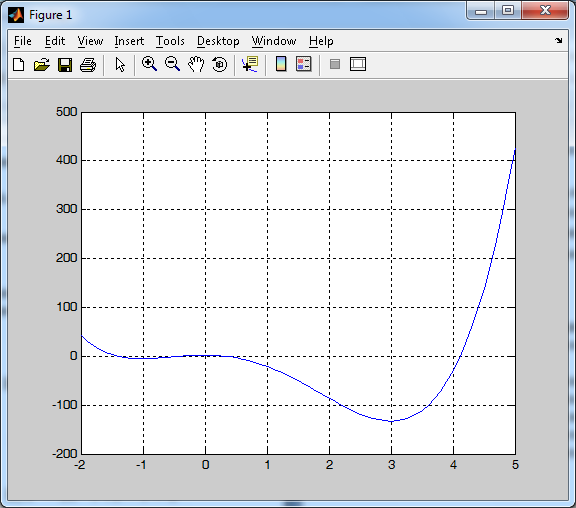
    Рисунок 3. График функции


    1. Уточним методом Бисекции корни уравнения, для этого создадим два м-файла с именами ex1.m , bisec.m


    function ex1

    % Решить уравнение f(x)=0,

    % Введём функцию f(x)

    f = inline('3*x.^4-8*x.^3-18*x.^2+2');

    root1 = bisec(f, -1.5, -0.4)

    root2 = bisec(f, -0.6, 0)

    root3 = bisec(f, 0, 0.5)

    root4 = bisec(f, 4.0, 4,3)
    function center = bisec(f, left, right)

    % Классический метод бисекции с точностью 2 eps

    while right - left > 0.0001

    center = (right - left) / 2 + left;

    if f(center) * f(left) > 0

    left = center;

    else

    right = center;

    end

    end


    1. Далее в командной строке введем ex1, и получим уточненные значения корней

    >> ex1

    root1 = -1.3933

    root2 = -0.3697

    root3 = 0.3145

    root4 = 4.1151


    1. Уточним методом Ньютона корни уравнения, для этого создадим два м-файла с именами ex2.m , newton.m

    function ex2

    % Решить уравнение f(x)=0, методом Ньютона

    % Введём функцию f(x)

    f = inline('3*x.^4-8*x.^3-18*x.^2+2');

    % Её производная

    df = inline('12*x.^3-24*x.^2-36*x');

    root1 = newton(f, df, -1)

    root2 = newton(f, df, -0.5)

    root3 = newton(f, df, 0.5)

    root4 = newton(f, df, 4.1)

    function root = newton(f, df, x0)

    root = x0 - f(x0) / df(x0);

    old_root = x0;

    while abs(old_root - root) > 2 * eps

    t = old_root;

    old_root = root;

    root = t - f(t) / df(t);

    end


    1. Далее в командной строке введем ex1, и получим уточненные значения корней

    root1 = Inf

    root2 = -0.3750

    root3 = 0.3528

    root4 = 4.1153
    Содержание отчета:

    1. Титульный лист.

    2. Цель лабораторной работы.

    3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

    4. Расчетная часть: описание выполнения задания в среде MatLab.

    5. Выводы и анализ полученных результатов.
    Контрольные вопросы:


    1. Этапы графического метода отделения корней нелинейного уравнения.

    2. Этапы аналитического метода отделения корней нелинейного уравнения

    3. Суть метод простых итераций(последовательных приближений).

    4. Суть метода Ньютона, уточнения корней нелинейного уравнения.

    5. Суть метод бисекций(половинного деления)

    6. Как создать M-файл?

    7. Как привести операторы М-файла к выполнению?

    8. Что означает данная запись abs(old_root - root) > 2 * eps в M-файле ?



    Лабораторная работа №5.

    «Решение систем линейных алгебраических уравнений»



    Цель работы: научиться вычислять корни систем линейных алгебраических уравнений различными методами.
    Задание 1:

    Решить систему линейных алгебраических уравнений с помощью:

    1. формул Крамера

    2. метода обратной матрицы.

    Предоставить в отчете результаты, как ручного решения, так и решение, реализованное в MatLab.
    Варианты заданий:
    4 x1 + 0,24 x2 – 0,08 x3 = 8;

    0,09x1 +3x2 – 0,15x3 = 9;

    0,04x1 – 0,08x2 + 4 x3 = 20.



    10 x1 +2 x2 + x3 = 35;

    x1+ 5 x2 + x3 = 29;

    2 x1 + 0,5 x2 + 4 x3 = 34.



    4 x1 + x2+ x3 = 24;

    x1 + 3 x2 + 2 x3 = – 10;

    2 x1 + x2 + 7 x3 = -28.



    7 x1 + 5 x2 + 2 x3 = 48;

    2 x1 + 10 x2 – x3 = 27;

    x1 + 2 x2– 3 x3 = 18.



    10 x1 + 2 x2 + x3 = 32;

    x1 + 5 x2 + x3 = 47;

    2 x1 + 0,5 x2+ 4 x3= 30.



    3,23x1+1,62x2+0,65x3=1,28

    1,62x1-2,33x2-1,43 x3=0,87

    0,65x1-1,43x2+2,18x3=-2,87





    14,38x1-2,41x2+1,39x3=5,86

    1,84x1-25,36x2-3,31x3=-2,28

    2,46x1-3,49x2+16,37x3=4,47



    2 x1– x2 + x3 = -3;

    3 x1 + 5 x2 – 2 x3 = 1;

    x1 – 4 x2 + 10 x3 = 0.



    5 x1 + x2 + 2 x3= 17;

    2 x1 + 7 x2 – x3 = -7;

    x1 – 2 x2 + 8 x3 = 36.



    5 x1 + 2 x2 -x3 = 19;

    x1 + 4 x2 + 2 x3 = 11;

    2 x1 + 3 x2 + 6 x3 = 21.



    2x1 + 0,5x2 + 0,5x3 = 12;

    x1 + 3 x2 + x3 = -4;

    3 x1 + 2 x2– 8 x3= 68.



    4 x1 – x2 –2 x3 = 15;

    3 x1 + 6 x2 – x3 = 19;

    x1 + 2 x2 + 3 x3 = 13.



    0,9x1+2,7x2-3,9 x3=2,41

    2,51x1+5,86x2+0,5x3=3,96

    4,45x1-2,27x2+3,9x3=-1,28



    2,3x1-4,21x2-11,61x3=14,41

    8,04x1+5,2x2+0,27x3=-6,44

    3,92x1-7,9x2+8,37x3=55,56



    2 x1– x2 + x3 = -3;

    3 x1 + 5 x2 – 2 x3 = 1;

    x1 – 4 x2 + 10 x3 = 0.

    • Смотрите также файлы