Файл: Пояснительная записка к расчетнографической работе по дисциплине "Теория вероятностей и математическая статистика".doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 79
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
5.Построение статистических оценок функции распределения
Статистическая функция распределения
Реализация статистической функции распределения F*(x) рассчитывается по формуле:
F*(x) =
где
Таким образом, график статистической функции распределения будет иметь следующий вид:
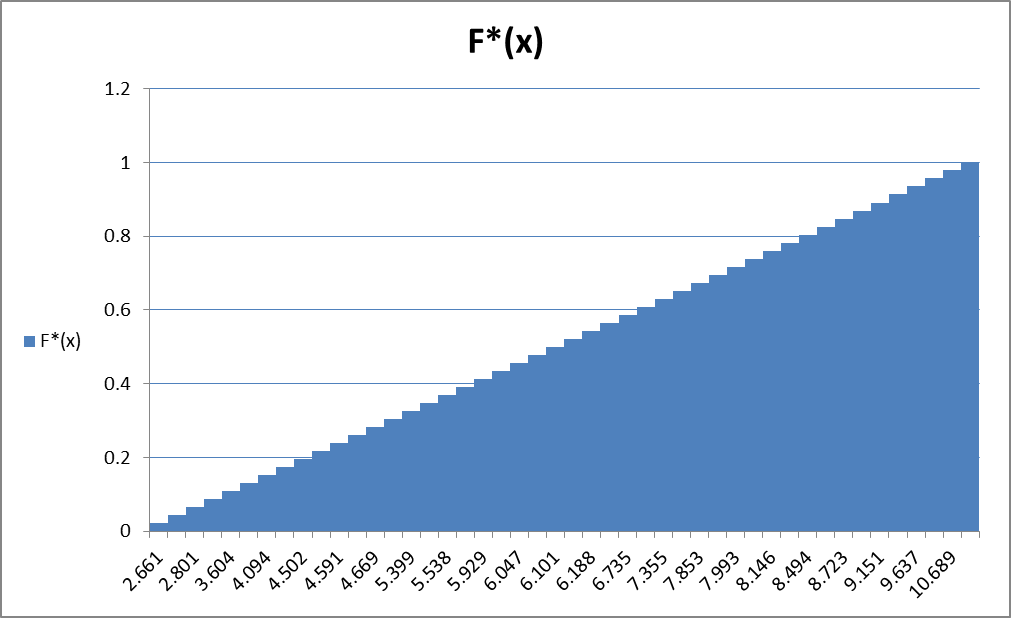 Рис.1 «График статистической функции распределения»
Рис.1 «График статистической функции распределения»Данные для построения статистической функции распределения приведены в приложении 4 (Критерий Колмогорова).
Кумулятивная ломаная
Кумулятивную ломаную (вторую оценку функции распределения) строим по формулам:
F** (x
F** (x
F** (x
……………………
F** (x
где
=1.
Результаты расчетов для построения кумулятивной ломаной из таблицы приложения 2 занесем в табл.4.
Таблица 4
| Номер интервала | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Границы интервалов | 2.661;3.861 | 3.861;5.061 | 5.061;6.261 | 6.261;7.461 | 7.461;8.661 | 8.661;9.861 | 9.861;11.061 |
| Относительная частота интервалов | 0.1304348 | 0.17391304 | 0.2391304 | 0.0869565 | 0.17391304 | 0.13043478 | 0.06521739 |
| F**(x) | 0.1304348 | 0.30434783 | 0.5434783 | 0.6304348 | 0.80434783 | 0.93478261 | 1 |
Таким образом, график кумулятивной ломаной будет иметь следующий вид:
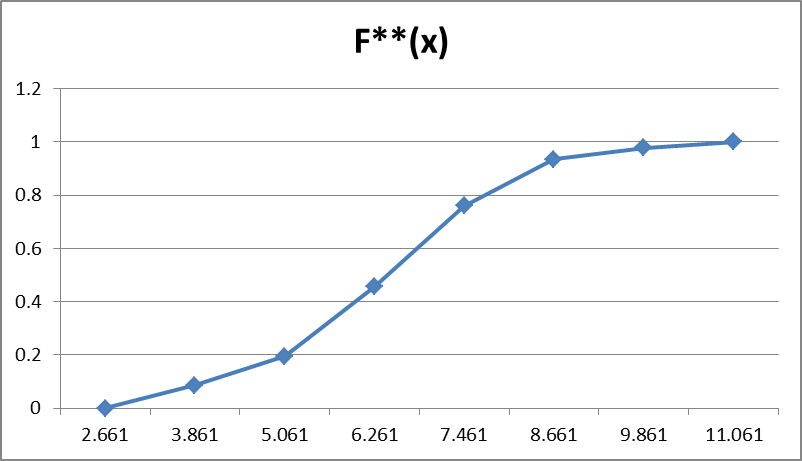
Рис.2 «График комулятивной ломаной»
6.Статистические оценки плотности распределения
Гистограммы относительных частот f*(x) и полигона частот f**(x)
Построим гистограмму на основе относительных частот.
Основаниями прямоугольников, из которых состоит гистограмма, служат интервалы длиной lj и высотой f*j.
Таким образом, гистограмма относительных частот строится следующим образом: на оси Оx отложим длины разрядов и на них, как на основаниях, построим прямоугольники, имеющие площадь p*j и высоту равную f*j.
Гистограмма изображена ниже:
Используем данные из табл. 3. “Статистический ряд” для построения оценок плотности распределения
f(x).
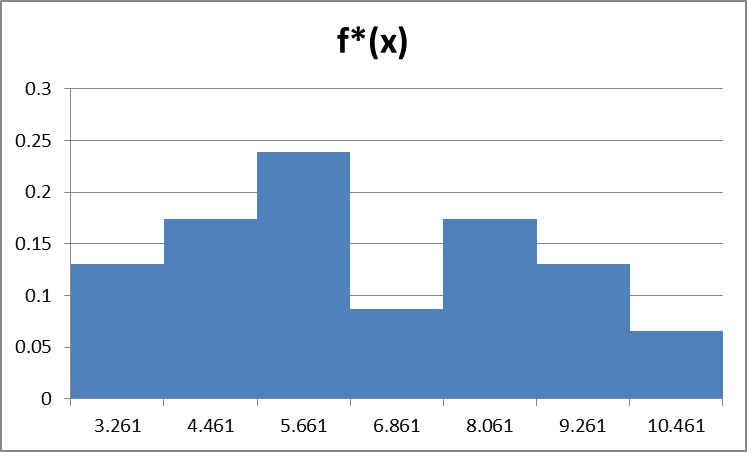
Рис.3. «Гистограмма относительных частот»
Полигон частот
Построим полигон частот (сглаженную гистограмму) – вторую оценку плотности распределения f(x). Полигон относительных частот строится по точкам (
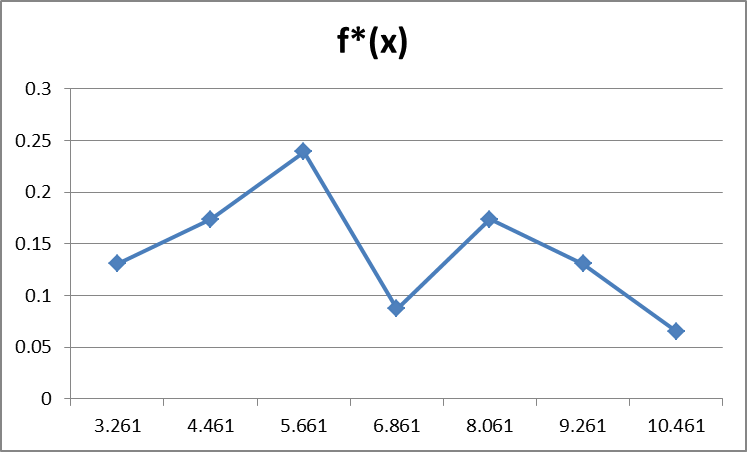
Рис.4 «Полигон относительных частот»
Полигон частот строим по точкам, координаты которых равны (
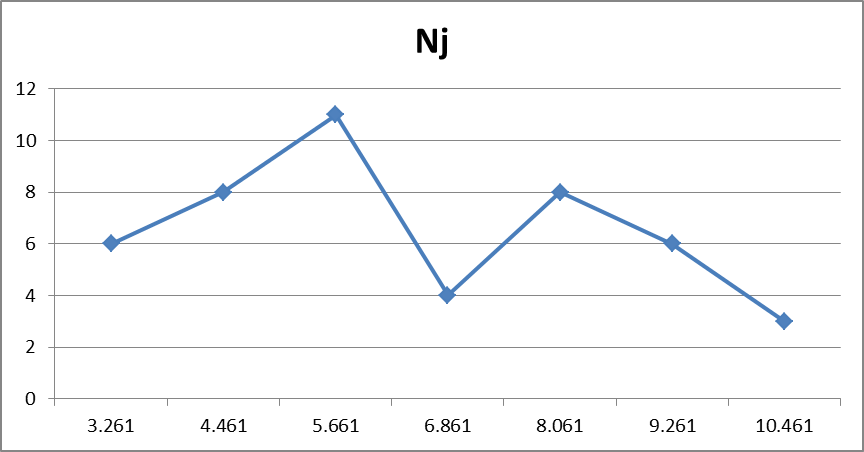
Рис.5 «Оценка плотности распределения по относительным частотам»
- 1 2 3 4 5 6 7
Проверка статистических гипотез о законе распределения СВ
-
Расчёты для проверки критерия согласия Колмогорова
Критерий Колмогорова позволяет проверить гипотезу о виде функции распределения случайной величины и ее параметрах. Выдвинем следующую гипотезу: случайная величина распределена по нормальному закону с функцией распределения
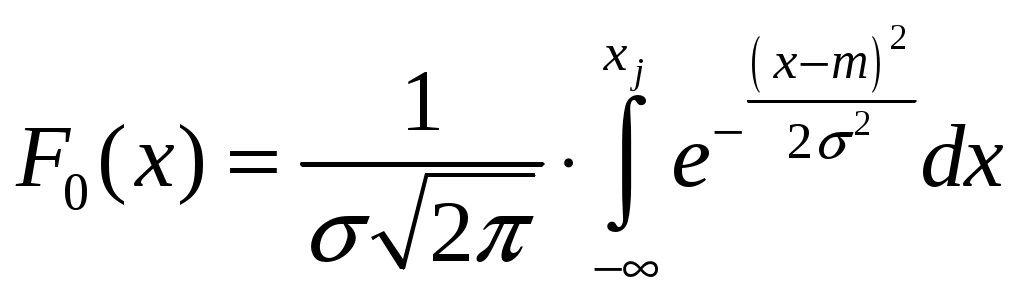 .
.В качестве оценок параметров нормального закона примем точечные оценки для математического ожидания и дисперсии:
Рассчитаем значение реализации статистики проверки гипотезы t: критерия Колмогорова по формуле:
где xi –элемент выборки,
Алгоритм проверки гипотезы:
-
Провести измерения Х и получить выборку хn; -
Построить вариационный ряд; -
Исключить грубые ошибки; -
Построить реализацию статистической функции распределения; -
Задать гипотезу, что F0(x) есть функция распределения Х; -
Рассчитать наблюдаемое значение критерия t, -
Задать значение уровня значимости а и с помощью таблицы Колмогорова найти критическое значение tα; -
Принять или отклонить гипотезу по правилу:
(
Зададим вероятность а=0,05 практически невозможного события, заключающегося в том, что оценка функции распределения отклонится от значения функции принятой в качестве гипотезы, на величину большую, чем tα P(
Значение параметра tα возьмем из таблицы Колмогорова (Приложение 5), исходя из значений вероятности а=0,05 и объема выборки n=46: tα=0,19625.
Наблюдаемое значение критерия (расчетное значение) получили t=0,0946, которое не превышает критического значения tα=0,19625. Следовательно, гипотеза о нормальном распределении случайной выборки принимается.
Расчёты критерия t представлены в Таблице №5.
Таблица 5
| | X | Y=(X-Xср)/S | Ф(y) | F0(x) | F*(x) | F*(x)-F0(x) |
| 1 | 2.661 | -1.736890105 | -0.4588 | 0.041203 | 0.021739 | 0.01946415 |
| 2 | 2.779 | -1.683082535 | -0.45382 | 0.04618 | 0.043478 | 0.0027013 |
| 3 | 2.801 | -1.673050616 | -0.45284 | 0.047159 | 0.065217 | 0.01805873 |
| 4 | 3.162 | -1.508435933 | -0.43428 | 0.065721 | 0.086957 | 0.02123503 |
| 5 | 3.604 | -1.306885545 | -0.40437 | 0.095626 | 0.108696 | 0.01306986 |
| 6 | 3.733 | -1.248062016 | -0.394 | 0.106004 | 0.130435 | 0.02443061 |
| 7 | 4.094 | -1.083447332 | -0.3607 | 0.139305 | 0.152174 | 0.01286895 |
| 8 | 4.213 | -1.029183767 | -0.3483 | 0.151697 | 0.173913 | 0.02221638 |
| 9 | 4.502 | -0.897400821 | -0.31525 | 0.184753 | 0.195652 | 0.01089964 |
| 10 | 4.505 | -0.896032832 | -0.31488 | 0.185118 | 0.217391 | 0.03227369 |
| 11 | 4.591 | -0.856817145 | -0.30423 | 0.195773 | 0.23913 | 0.04335746 |
| 12 | 4.662 | -0.824441404 | -0.29516 | 0.204844 | 0.26087 | 0.05602517 |
| 13 | 4.669 | -0.82124943 | -0.29425 | 0.205752 | 0.282609 | 0.07685659 |
| 14 | 4.888 | -0.721386229 | -0.26466 | 0.235336 | 0.304348 | 0.06901187 |
| 15 | 5.399 | -0.488372093 | -0.18736 | 0.312643 | 0.326087 | 0.0134438 |
| 16 | 5.421 | -0.478340173 | -0.1838 | 0.316204 | 0.347826 | 0.03162203 |
| 17 | 5.538 | -0.4249886 | -0.16458 | 0.335422 | 0.369565 | 0.03414272 |
| 18 | 5.912 | -0.254445964 | -0.10042 | 0.399576 | 0.391304 | 0.00827117 |
| 19 | 5.929 | -0.246694026 | -0.09743 | 0.402573 | 0.413043 | 0.01047096 |
| 20 | 6 | -0.214318285 | -0.08485 | 0.415149 | 0.434783 | 0.01963318 |
| 21 | 6.047 | -0.192886457 | -0.07648 | 0.423524 | 0.456522 | 0.03299779 |
| 22 | 6.065 | -0.184678523 | -0.07326 | 0.426741 | 0.478261 | 0.05152027 |
| 23 | 6.101 | -0.168262654 | -0.06681 | 0.433188 | 0.5 | 0.06681167 |
| 24 | 6.122 | -0.158686731 | -0.06304 | 0.436958 | 0.521739 | 0.08478128 |
| 25 | 6.188 | -0.128590971 | -0.05116 | 0.448841 | 0.543478 | 0.09463761 |
| 26 | 6.422 | -0.021887825 | -0.00873 | 0.491269 | 0.565217 | 0.07394867 |
| 27 | 6.735 | 0.120839033 | 0.048091 | 0.548091 | 0.586957 | 0.03886579 |
| 28 | 7.196 | 0.331053352 | 0.129698 | 0.629698 | 0.608696 | 0.02100225 |
| 29 | 7.355 | 0.403556772 | 0.156731 | 0.656731 | 0.630435 | 0.02629588 |
| 30 | 7.631 | 0.529411765 | 0.20174 | 0.70174 | 0.652174 | 0.04956617 |
| 31 | 7.853 | 0.630642955 | 0.235863 | 0.735863 | 0.673913 | 0.06194995 |
| 32 | 7.955 | 0.677154583 | 0.250846 | 0.750846 | 0.695652 | 0.05519389 |
| 33 | 7.993 | 0.694482444 | 0.25631 | 0.75631 | 0.717391 | 0.03891884 |
| 34 | 7.997 | 0.69630643 | 0.256882 | 0.756882 | 0.73913 | 0.01775109 |
| 35 | 8.146 | 0.764249886 | 0.277641 | 0.777641 | 0.76087 | 0.01677126 |
| 36 | 8.324 | 0.845417237 | 0.301061 | 0.801061 | 0.782609 | 0.01845234 |
| 37 | 8.494 | 0.922936617 | 0.32198 | 0.82198 | 0.804348 | 0.01763206 |
| 38 | 8.634 | 0.986776106 | 0.338124 | 0.838124 | 0.826087 | 0.01203684 |
| 39 | 8.723 | 1.027359781 | 0.347874 | 0.847874 | 0.847826 | 4.8372E-05 |
| 40 | 8.898 | 1.107159143 | 0.365887 | 0.865887 | 0.869565 | 0.00367778 |
| 41 | 9.151 | 1.22252622 | 0.389246 | 0.889246 | 0.891304 | 0.0020587 |
| 42 | 9.44 | 1.354309166 | 0.412181 | 0.912181 | 0.913043 | 0.00086236 |
| 43 | 9.637 | 1.444140447 | 0.42565 | 0.92565 | 0.934783 | 0.00913235 |
| 44 | 9.666 | 1.457364341 | 0.427492 | 0.927492 | 0.956522 | 0.02902966 |
| 45 | 10.689 | 1.923848609 | 0.472813 | 0.972813 | 0.978261 | 0.00544765 |
| 46 | 11.054 | 2.090287278 | 0.481704 | 0.981704 | 1 | 0.018296 |
| | | | | | max | 0.09463761 |
| | | | | | tкр | 0.19625 |