Файл: Пояснительная записка к расчетнографической работе по дисциплине "Теория вероятностей и математическая статистика".doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 84
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Выводы
В результате выполненных расчётов было установлено следующее:
-
При проведении опыта не были выявлены грубые ошибки измерения.
-
Точечные оценки математического ожидания и дисперсии исследуемой случайной величины соответственно равны:
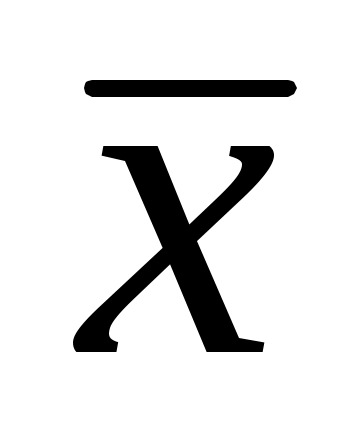 =6,47;
=6,47; 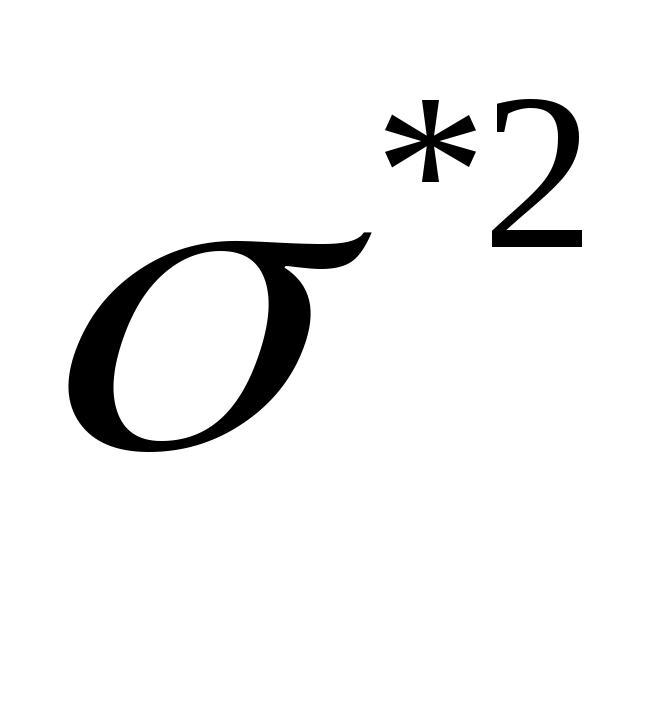 =4,809.
=4,809.
3. В результате проведенной проверки соответствия закона распределения случайной величины – время загрузки игрового сервера – нормальному закону, было установлено, что с вероятностью 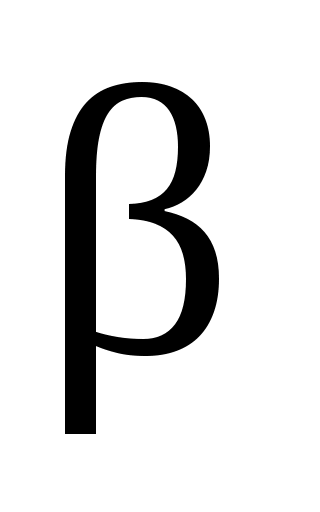 = 0,95 практически достоверного события выборочные данные согласуются с гипотезой о нормальном законе распределения исследуемого показателя.
= 0,95 практически достоверного события выборочные данные согласуются с гипотезой о нормальном законе распределения исследуемого показателя.
Conclusions
As a result of the calculations, the following was done:
1. During the experiment, gross measurement errors were not revealed.
2. Point estimates of the mathematical expectation and variance of the random variable under study are:
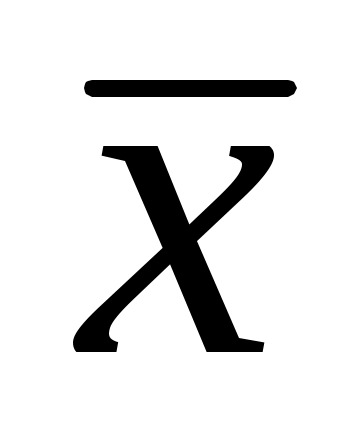 = 15,4358;
= 15,4358; 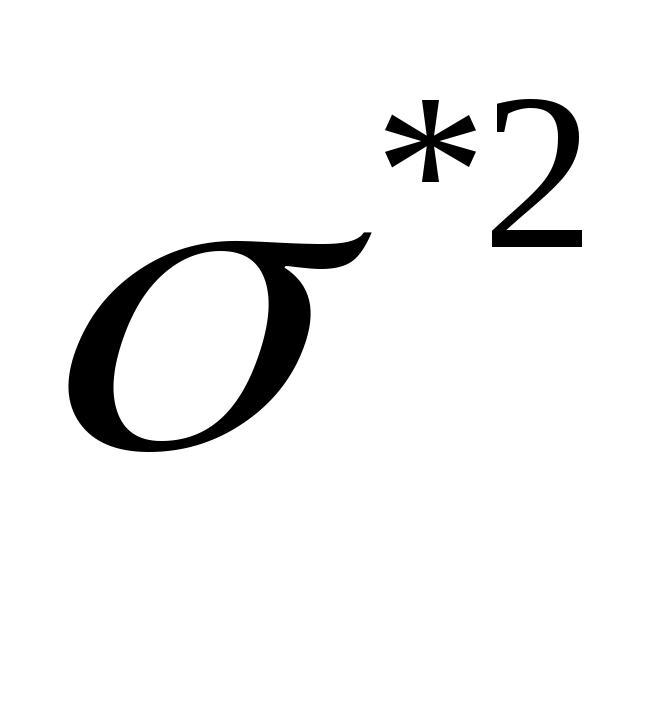 = 1,6545933.
= 1,6545933.
-
As a result of the verification of the correspondence of the law of distribution of a random variable — the load time of the game server — to the normal law, it was found that with probability = 0.95 of a practically reliable event, the selected data are consistent with the hypothesis of a normal distribution law of the indicator under study.
Список литературы
-
Нейман, Ю. Вводный курс теории вероятностей и математической статистики [Текст] / Пер. с. англ. Н. М. Митрофановой и А. П. Хусу ; Под ред. акад. Ю. В. Линника. - Москва : Наука, 1968. - 448 с. : черт.; 20 см.
-
Роднищев Н.Е. Теория вероятностей : учеб. пособие/ Н. Е. Роднищев; Мин-во образ-я и науки РФ, ФГБОУ ВПО КНИТУ-КАИ им. А.Н. Туполева. -Казань: Изд-во КНИТУ-КАИ, 2014. – 136 с.
-
Сидняев, Н. И. Теория планирования эксперимента и анализ статистических данных : учеб. пособие для магистров / Н. И. Сидняев. – М. : Юрайт, 2012. – 399 с.
-
Буре, В.М. Теория вероятностей и математическая статистика. [Электронный ресурс] : Учебники / В.М. Буре, Е.М. Парилина. — Электрон. дан. — СПб. : Лань, 2013. — 416 с. — Режим доступа: http://e.lanbook.com/book/10249.
-
Гусак, А.А. Теория вероятностей: справочное пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – Минск : ТетраСистемс, 2008.
-
William Feller. An Introduction to Probability Theory and Its Applications, Volume 1. January 15th 1968 by Wiley. – 528.
-
Sheldon M. Ross. A First Course in Probability. May 28th 2005 by Prentice Hall. – 576.
-
Kai Chung. A Course in Probability Theory 2nd Edition. Academic Press. 28th June 2014 – 365.
Приложения
Приложение 1. Исключение грубых ошибок
Выводы
В результате выполненных расчётов было установлено следующее:
-
При проведении опыта не были выявлены грубые ошибки измерения.
-
Точечные оценки математического ожидания и дисперсии исследуемой случайной величины соответственно равны:
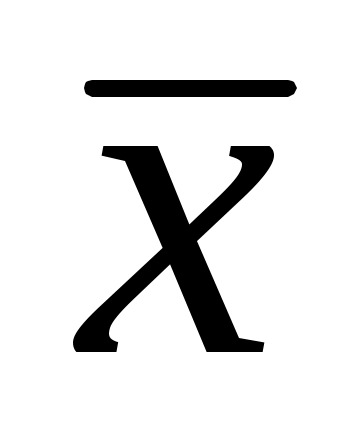 =6,47;
=6,47; 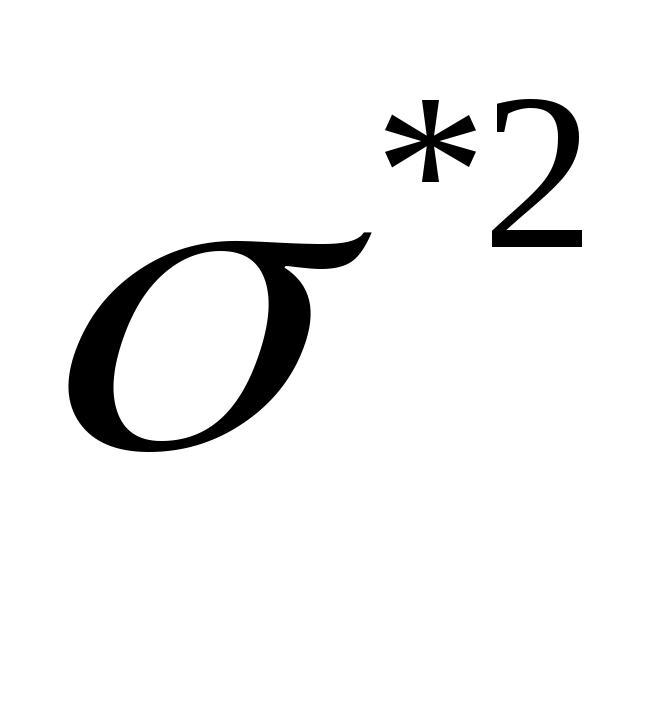 =4,809.
=4,809.
3. В результате проведенной проверки соответствия закона распределения случайной величины – время загрузки игрового сервера – нормальному закону, было установлено, что с вероятностью 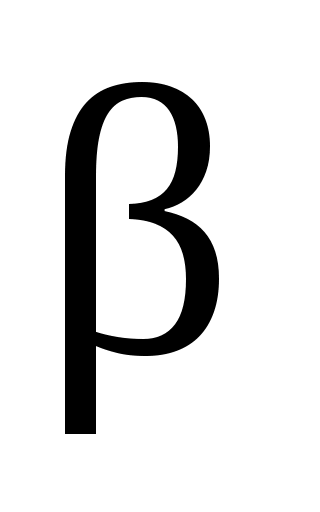 = 0,95 практически достоверного события выборочные данные согласуются с гипотезой о нормальном законе распределения исследуемого показателя.
= 0,95 практически достоверного события выборочные данные согласуются с гипотезой о нормальном законе распределения исследуемого показателя.
Conclusions
As a result of the calculations, the following was done:
1. During the experiment, gross measurement errors were not revealed.
2. Point estimates of the mathematical expectation and variance of the random variable under study are:
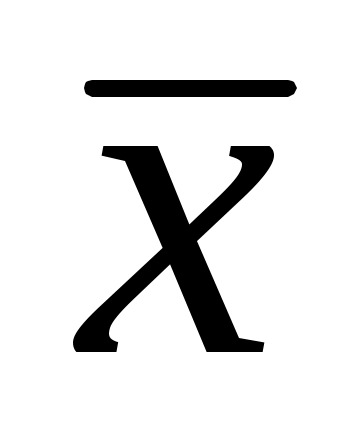 = 15,4358;
= 15,4358; 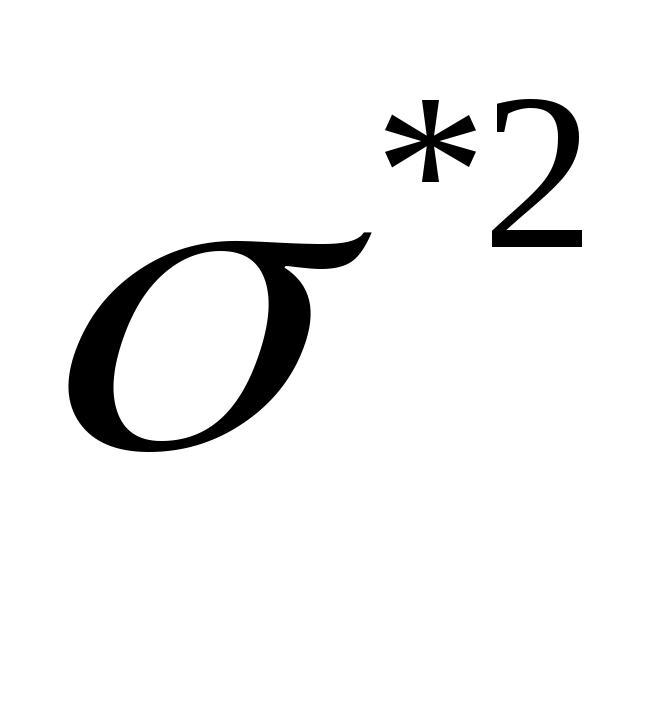 = 1,6545933.
= 1,6545933.
-
As a result of the verification of the correspondence of the law of distribution of a random variable — the load time of the game server — to the normal law, it was found that with probability = 0.95 of a practically reliable event, the selected data are consistent with the hypothesis of a normal distribution law of the indicator under study.
Список литературы
-
Нейман, Ю. Вводный курс теории вероятностей и математической статистики [Текст] / Пер. с. англ. Н. М. Митрофановой и А. П. Хусу ; Под ред. акад. Ю. В. Линника. - Москва : Наука, 1968. - 448 с. : черт.; 20 см.
-
Роднищев Н.Е. Теория вероятностей : учеб. пособие/ Н. Е. Роднищев; Мин-во образ-я и науки РФ, ФГБОУ ВПО КНИТУ-КАИ им. А.Н. Туполева. -Казань: Изд-во КНИТУ-КАИ, 2014. – 136 с.
-
Сидняев, Н. И. Теория планирования эксперимента и анализ статистических данных : учеб. пособие для магистров / Н. И. Сидняев. – М. : Юрайт, 2012. – 399 с.
-
Буре, В.М. Теория вероятностей и математическая статистика. [Электронный ресурс] : Учебники / В.М. Буре, Е.М. Парилина. — Электрон. дан. — СПб. : Лань, 2013. — 416 с. — Режим доступа: http://e.lanbook.com/book/10249.
-
Гусак, А.А. Теория вероятностей: справочное пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – Минск : ТетраСистемс, 2008.
-
William Feller. An Introduction to Probability Theory and Its Applications, Volume 1. January 15th 1968 by Wiley. – 528.
-
Sheldon M. Ross. A First Course in Probability. May 28th 2005 by Prentice Hall. – 576.
-
Kai Chung. A Course in Probability Theory 2nd Edition. Academic Press. 28th June 2014 – 365.
Приложения
Приложение 1. Исключение грубых ошибок
Выводы
В результате выполненных расчётов было установлено следующее:
-
При проведении опыта не были выявлены грубые ошибки измерения. -
Точечные оценки математического ожидания и дисперсии исследуемой случайной величины соответственно равны:
3. В результате проведенной проверки соответствия закона распределения случайной величины – время загрузки игрового сервера – нормальному закону, было установлено, что с вероятностью
Conclusions
As a result of the calculations, the following was done:
1. During the experiment, gross measurement errors were not revealed.
2. Point estimates of the mathematical expectation and variance of the random variable under study are:
-
As a result of the verification of the correspondence of the law of distribution of a random variable — the load time of the game server — to the normal law, it was found that with probability = 0.95 of a practically reliable event, the selected data are consistent with the hypothesis of a normal distribution law of the indicator under study.
Список литературы
-
Нейман, Ю. Вводный курс теории вероятностей и математической статистики [Текст] / Пер. с. англ. Н. М. Митрофановой и А. П. Хусу ; Под ред. акад. Ю. В. Линника. - Москва : Наука, 1968. - 448 с. : черт.; 20 см. -
Роднищев Н.Е. Теория вероятностей : учеб. пособие/ Н. Е. Роднищев; Мин-во образ-я и науки РФ, ФГБОУ ВПО КНИТУ-КАИ им. А.Н. Туполева. -Казань: Изд-во КНИТУ-КАИ, 2014. – 136 с. -
Сидняев, Н. И. Теория планирования эксперимента и анализ статистических данных : учеб. пособие для магистров / Н. И. Сидняев. – М. : Юрайт, 2012. – 399 с. -
Буре, В.М. Теория вероятностей и математическая статистика. [Электронный ресурс] : Учебники / В.М. Буре, Е.М. Парилина. — Электрон. дан. — СПб. : Лань, 2013. — 416 с. — Режим доступа: http://e.lanbook.com/book/10249. -
Гусак, А.А. Теория вероятностей: справочное пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – Минск : ТетраСистемс, 2008. -
William Feller. An Introduction to Probability Theory and Its Applications, Volume 1. January 15th 1968 by Wiley. – 528. -
Sheldon M. Ross. A First Course in Probability. May 28th 2005 by Prentice Hall. – 576. -
Kai Chung. A Course in Probability Theory 2nd Edition. Academic Press. 28th June 2014 – 365.
Приложения
Приложение 1. Исключение грубых ошибок
| | | x-x | (x-x)2 |
| 1 | 2.661 | -3.809 | 14.50848 |
| 2 | 2.779 | -3.691 | 13.62348 |
| 3 | 2.801 | -3.669 | 13.46156 |
| 4 | 3.162 | -3.308 | 10.94286 |
| 5 | 3.604 | -2.866 | 8.213956 |
| 6 | 3.733 | -2.737 | 7.491169 |
| 7 | 4.094 | -2.376 | 5.645376 |
| 8 | 4.213 | -2.257 | 5.094049 |
| 9 | 4.502 | -1.968 | 3.873024 |
| 10 | 4.505 | -1.965 | 3.861225 |
| 11 | 4.591 | -1.879 | 3.530641 |
| 12 | 4.662 | -1.808 | 3.268864 |
| 13 | 4.669 | -1.801 | 3.243601 |
| 14 | 4.888 | -1.582 | 2.502724 |
| 15 | 5.399 | -1.071 | 1.147041 |
| 16 | 5.421 | -1.049 | 1.100401 |
| 17 | 5.538 | -0.932 | 0.868624 |
| 18 | 5.912 | -0.558 | 0.311364 |
| 19 | 5.929 | -0.541 | 0.292681 |
| 20 | 6 | -0.47 | 0.2209 |
| 21 | 6.047 | -0.423 | 0.178929 |
| 22 | 6.065 | -0.405 | 0.164025 |
| 23 | 6.101 | -0.369 | 0.136161 |
| 24 | 6.122 | -0.348 | 0.121104 |
| 25 | 6.188 | -0.282 | 0.079524 |
| 26 | 6.422 | -0.048 | 0.002304 |
| 27 | 6.735 | 0.265 | 0.070225 |
| 28 | 7.196 | 0.726 | 0.527076 |
| 29 | 7.355 | 0.885 | 0.783225 |
| 30 | 7.631 | 1.161 | 1.347921 |
| 31 | 7.853 | 1.383 | 1.912689 |
| 32 | 7.955 | 1.485 | 2.205225 |
| 33 | 7.993 | 1.523 | 2.319529 |
| 34 | 7.997 | 1.527 | 2.331729 |
| 35 | 8.146 | 1.676 | 2.808976 |
| 36 | 8.324 | 1.854 | 3.437316 |
| 37 | 8.494 | 2.024 | 4.096576 |
| 38 | 8.634 | 2.164 | 4.682896 |
| 39 | 8.723 | 2.253 | 5.076009 |
| 40 | 8.898 | 2.428 | 5.895184 |
| 41 | 9.151 | 2.681 | 7.187761 |
| 42 | 9.44 | 2.97 | 8.8209 |
| 43 | 9.637 | 3.167 | 10.02989 |
| 44 | 9.666 | 3.196 | 10.21442 |
| 45 | 10.689 | 4.219 | 17.79996 |
| 46 | 11.054 | 4.584 | 21.01306 |
| | | | |
| Xср | 6.47 | | 216.4446 |
| | | | 4.809881 |
| | | S | 2.193144 |
| | | ta | 2.956 |
| | | | |
| | Xmin> | -0.01383 | |
| | Xmax> | 12.952 | |
Приложение 2. Интервальная таблица
| Номер интервала | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Границы интервалов | 2.661;3.861 | 3.861;5.061 | 5.061;6.261 | 6.261;7.461 | 7.461;8.661 | 8.661;9.861 | 9.861;11.061 |
| Длина интервалов | 1.2 | 1.2 | 1.2 | 1.2 | 1.2 | 1.2 | 1.2 |
| Частота интервала | 6 | 8 | 11 | 4 | 8 | 6 | 3 |
| Относительная частота интервалов | 0.1304348 | 0.17391304 | 0.2391304 | 0.0869565 | 0.17391304 | 0.13043478 | 0.06521739 |
| Плотность относительной частоты | 0.1086957 | 0.14492754 | 0.1992754 | 0.0724638 | 0.14492754 | 0.10869565 | 0.05434783 |
| Середина интервала | 3.261 | 4.461 | 5.661 | 6.861 | 8.061 | 9.261 | 10.461 |
| F**(x) | 0.1304348 | 0.30434783 | 0.5434783 | 0.6304348 | 0.80434783 | 0.93478261 | 1 |
Приложение 3. Точечные и интервальные оценки математического ожидания и дисперсии
| | | x-x | (x-x)2 | | | | | |
| 1 | 2.661 | -3.809 | 14.50848 | | | | | |
| 2 | 2.779 | -3.691 | 13.62348 | | | | | |
| 3 | 2.801 | -3.669 | 13.46156 | | | | | |
| 4 | 3.162 | -3.308 | 10.94286 | | | | | |
| 5 | 3.604 | -2.866 | 8.213956 | | | | | |
| 6 | 3.733 | -2.737 | 7.491169 | | | | | |
| 7 | 4.094 | -2.376 | 5.645376 | | | | | |
| 8 | 4.213 | -2.257 | 5.094049 | | | | | |
| 9 | 4.502 | -1.968 | 3.873024 | | | | | |
| 10 | 4.505 | -1.965 | 3.861225 | | | | | |
| 11 | 4.591 | -1.879 | 3.530641 | | | | | |
| 12 | 4.662 | -1.808 | 3.268864 | | | | | |
| 13 | 4.669 | -1.801 | 3.243601 | | | | | |
| 14 | 4.888 | -1.582 | 2.502724 | | | | | |
| 15 | 5.399 | -1.071 | 1.147041 | | | | | |
| 16 | 5.421 | -1.049 | 1.100401 | | | | | |
| 17 | 5.538 | -0.932 | 0.868624 | | | | | |
| 18 | 5.912 | -0.558 | 0.311364 | | | | | |
| 19 | 5.929 | -0.541 | 0.292681 | | | | | |
| 20 | 6 | -0.47 | 0.2209 | | | | | |
| 21 | 6.047 | -0.423 | 0.178929 | | | | | |
| 22 | 6.065 | -0.405 | 0.164025 | | | | | |
| 23 | 6.101 | -0.369 | 0.136161 | | | | | |
| 24 | 6.122 | -0.348 | 0.121104 | | | | | |
| 25 | 6.188 | -0.282 | 0.079524 | | | | | |
| 26 | 6.422 | -0.048 | 0.002304 | | | | | |
| 27 | 6.735 | 0.265 | 0.070225 | | | | | |
| 28 | 7.196 | 0.726 | 0.527076 | | | | | |
| 29 | 7.355 | 0.885 | 0.783225 | | | | | |
| 30 | 7.631 | 1.161 | 1.347921 | | | | | |
| 31 | 7.853 | 1.383 | 1.912689 | | | | | |
| 32 | 7.955 | 1.485 | 2.205225 | | | | | |
| 33 | 7.993 | 1.523 | 2.319529 | | | | | |
| 34 | 7.997 | 1.527 | 2.331729 | | | | | |
| 35 | 8.146 | 1.676 | 2.808976 | | | | | |
| 36 | 8.324 | 1.854 | 3.437316 | | | | | |
| 37 | 8.494 | 2.024 | 4.096576 | | | | | |
| 38 | 8.634 | 2.164 | 4.682896 | | | | | |
| 39 | 8.723 | 2.253 | 5.076009 | | | | | |
| 40 | 8.898 | 2.428 | 5.895184 | | | | | |
| 41 | 9.151 | 2.681 | 7.187761 | | | | | |
| 42 | 9.44 | 2.97 | 8.8209 | | | | | |
| 43 | 9.637 | 3.167 | 10.02989 | | | | | |
| 44 | 9.666 | 3.196 | 10.21442 | | | | | |
| 45 | 10.689 | 4.219 | 17.79996 | | | | | |
| 46 | 11.054 | 4.584 | 21.01306 | | | | | |
| | | | | | | | | |
| Xср | 6.47 | | 216.4446 | | tas | 2.014 | | |
| | | | 4.809881 | | | | | |
| | | S | 2.193144 | | m1 | 5.810662 | χ1 | 28.366 |
| | | | | | m2 | 7.127555 | χ2 | 65.41 |
| | | | | | | | | |
| | | | | | σ21 | 3.382579 | | |
| | | | | | σ22 | 7.79999 | | |
Приложение 4. Таблица значений функции F(x)=
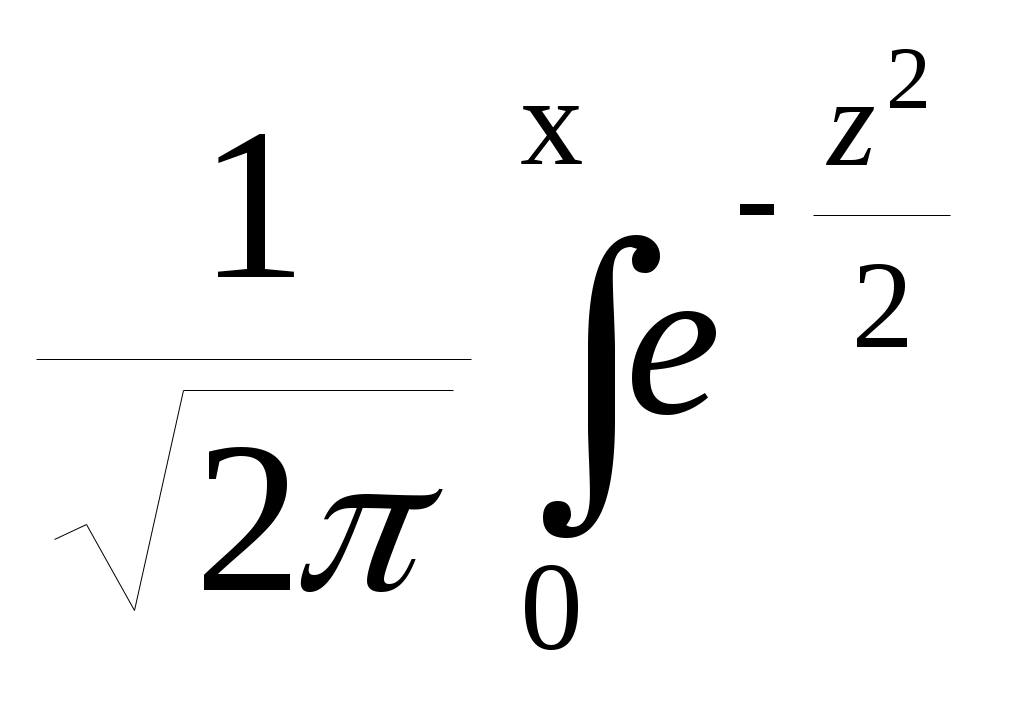 dz
dz| X | Ф (X) | X | Ф (х) | X | Ф (X) | X | Ф (х) |
| 1,26 | 0,3962 | 1,59 | 0,4441 | 1,92 | 0,4726 | 2,50 | 0,4938 |
| 1,27 | 0,3980 | 1,60 | 0,4452 | 1,93 | 0,4732 | 2,52 | 0,4941 |
| 1,28 | 0,3997 | 1,61 | 0,4463 | 1,94 | 0,4738 | 2,54 | 0,4945 |
| 1,29 | 0,4015 | 1,62 | 0,4474 | 1,95 | 0,4744 | 2,56 | 0,4948 |
| 1,30 | 0,4032 | 1,63 | 0,4484 | 1,96 | 0,4750 | 2,58 | 0,4951 |
| 1,31 | 0,4049 | 1,64 | 0,4495 | 1,97 | 0,4756 | 2,60 | 0,4953 |
| 1,32 | 0,4066 | 1,65 | 0,4505 | 1,98 | 0,4761 | 2,62 | 0,4956 |
| 1,33 | 0,4082 | 1,66 | 0,4515 | 1,99 | 0,4767 | 2,64 | 0,4959 |
| 1,34 | 0,4099 | 1,67 | 0,4525 | 2,00 | 0,4772 | 2,66 | 0,4961 |
| 1,35 | 0,4115 | 1,68 | 0,4535 | 2,02 | 0,4783 | 2,68 | 0,4963 |
| 1,36 | 0,4131 | 1,69 | 0,4545 | 2,04 | 0,4793 | 2,70 | 0,4965 |
| 1,37 | 0,4147 | 1,70 | 0,4554 | 2,06 | 0,4803 | 2,72 | 0,4967 |
| 1,38 | 0,4162 | 1,71 | 0,4564 | 2,08 | 0,4812 | 2,74 | 0,4969 |
| 1,39 | 0,4177 | 1,72 | 0,4573 | 2,10 | 0,4821 | 2,76 | 0,4971 |
| 1,40 | 0,4192 | 1,73 | 0,4582 | 2,12 | 0,4830 | 2,78 | 0,4973 |
| 1,41 | 0,4207 | 1,74 | 0,4591 | 2,14 | 0,4838 | 2,80 | 0,4974 |
| 1,42 | 0,4222 | 1,75 | 0,4599 | 2,16 | 0,4846 | 2,82 | 0,4976 |
| 1,43 | 0,4236 | 1,76 | 0,4608 | 2,18 | 0,4854 | 2,84 | 0,4977 |
| 1,44 | 0,4251 | 1,77 | 0,4616 | 2,20 | 0,4861 | 2,86 | 0,4979 |
| 1,45 | 0,4265 | 1,78 | 0,4625 | 2,22 | 0,4868 | 2,88 | 0,4980 |
| 1,46 | 0,4279 | 1,79 | 0,4633 | 2,24 | 0,4875 | 2,90 | 0,4981 |
| 1,47 | 0,4292 | 1,80 | 0,4641 | 2,26 | 0,4881 | 2,92 | 0,4982 |
| 1,48 | 0,4306 | 1,81 | 0,4649 | 2,28 | 0,4887 | 2,94 | 0,4984 |
| 1,49 | 0,4319 | 1,82 | 0,4656 | 2,30 | 0,4893 | 2,96 | 0,4985 |
| 1,50 | 0,4332 | 1,83 | 0,4664 | 2,32 | 0,4898 | 2,98 | 0,4986 |
| 1,51 | 0,4345 | 1,84 | 0,4671 | 2,34 | 0,4904 | 3,00 | 0,49865 |
| 1,52 | 0,4357 | 1,85 | 0,4678 | 2,36 | 0,4909 | 3,20 | 0,49931 |
| 1,53 | 0,4370 | 1,86 | 0,4686 | 2,38 | 0,4913 | 3,40 | 0,49966 |
| 1,54 | 0,4382 | 1,87 | 0,4693 | 2,40 | 0,4918 | 3,60 | 0,499841 |
| 1,55 | 0,4394 | 1,88 | 0,4699 | 2,42 | 0,4922 | 3,80 | 0,499928 |
| 1,56 | 0,4406 | 1,89 | 0,4706 | 2,44 | 0,4927 | 4,00 | 0,499968 |
| 1,57 | 0,4418 | 1,90 | 0,4713 | 2,46 | 0,4931 | 4,50 | 0,499997 |
| 1,58 | 0,4429 | 1,91 | 0,4719 | 2,48 | 0,4934 | 5,00 | 0,499997 |