Файл: Пояснительная записка к расчетнографической работе по дисциплине "Теория вероятностей и математическая статистика".doc

Первичная обработка результатов измерений

1.Построение вариационного ряда

Строим вариационный ряд, т.е. упорядочиваем элементы выборки x₁, …, x_n в порядке неубывания. Полученный вариационный ряд представлен в Таблице 2.

Таблица 2

№	Значение	№ измерения	Значение
1	2.661	24	6.122
2	2.779	25	6.188
3	2.801	26	6.422
4	3.162	27	6.735
5	3.604	28	7.196
6	3.733	29	7.355
7	4.094	30	7.631
8	4.213	31	7.853
9	4.502	32	7.955
10	4.505	33	7.993
11	4.591	34	7.997
12	4.662	35	8.146
13	4.669	36	8.324
14	4.888	37	8.494
15	5.399	38	8.634
16	5.421	39	8.723
17	5.538	40	8.898
18	5.912	41	9.151
19	5.929	42	9.44
20	6	43	9.637
21	6.047	44	9.666
22	6.065	45	10.689
23	6.101	46	11.054

---

2.Исключение грубых ошибок измерений

Выполним проверку выборки измерений на наличие грубых ошибок измерений. Для этого:

1. На основе данных об уровне значимости α =0,05 и начальном объеме выборки n=46 из таблицы Приложения 10 по входам n и α выбираем значение параметра t_α= 2,956.

2. Определим значения минимального и максимального элементов выборки, подлежащие проверке:

x₍₁₎ =x_min =2,661

x_(n) = x_max = 11,054.

3. Находим выборочное среднее: = =6,47.

4. Находим значение параметра s: s = 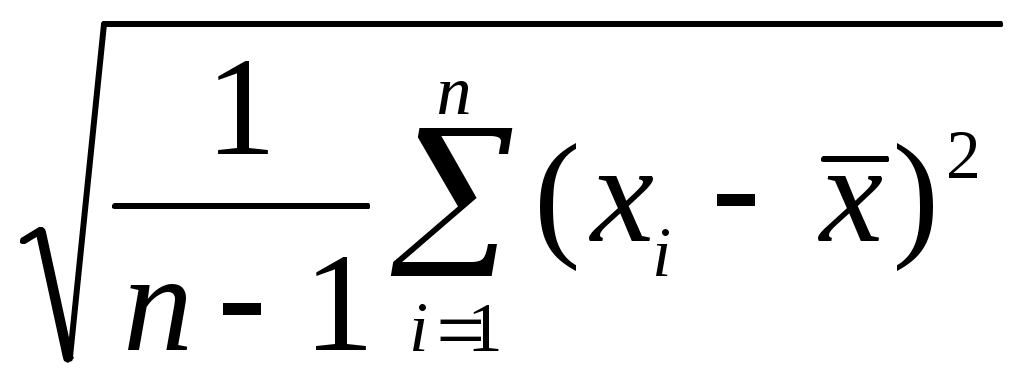= 2,193.

5. Выполняем проверку минимального элемента вариационного ряда на грубую ошибку:

Сравним x_min^*₌ -st_α=-0,013 c x_min=2,661, x_min> -st_α ,следовательно, х_min=2,661 не является грубой ошибкой.

6. Выполняем проверку максимального элемента вариационного ряда на грубую ошибку:
Сравним x_max^*₌ +st_α =12,952 с x_max=11,054, x_max< +st_α, следовательно, x_max=12,952 не является грубой ошибкой и остаётся в выборке.

Расчеты по данному алгоритму приведены в Приложении 1.

---

Таким образом, грубых ошибок в выборке нет. Заканчиваем их поиск.

После выполнения алгоритма выявления грубых ошибок объем выборки остался: n=46. Соответственно, и s не изменились. Вариационный ряд так же не изменился.

3.Построение статистических оценок математического ожидания и дисперсии

Расчет реализаций точечных оценок параметров распределения
Рассчитаем реализацию точечной оценки математического ожидания (выборочное среднее):

= =6,47 .

Если математическое ожидание m неизвестно, то в качестве математического ожидания берется его точечная оценка (выборочное среднее). Рассчитаем реализацию точечной оценки дисперсии (исправленную выборочную дисперсию):

= = 4,809.
Расчет интервальных оценок параметров распределения
Доверительная вероятность, с которой доверительный интервал накроет истинное значение параметра закона распределения случайной величины:

β =1 – α = 0,95.

Рассчитаем границы доверительного интервала для математического ожидания.

Реализация точечной оценки математического ожидания известна (рассчитана в предыдущем пункте).

Из таблиц распределения Стьюдента по значениям k=(n-1)=45 и α =0,05 находим значение :

=2,014.

Границы доверительного интервала для математического ожидания

---

:

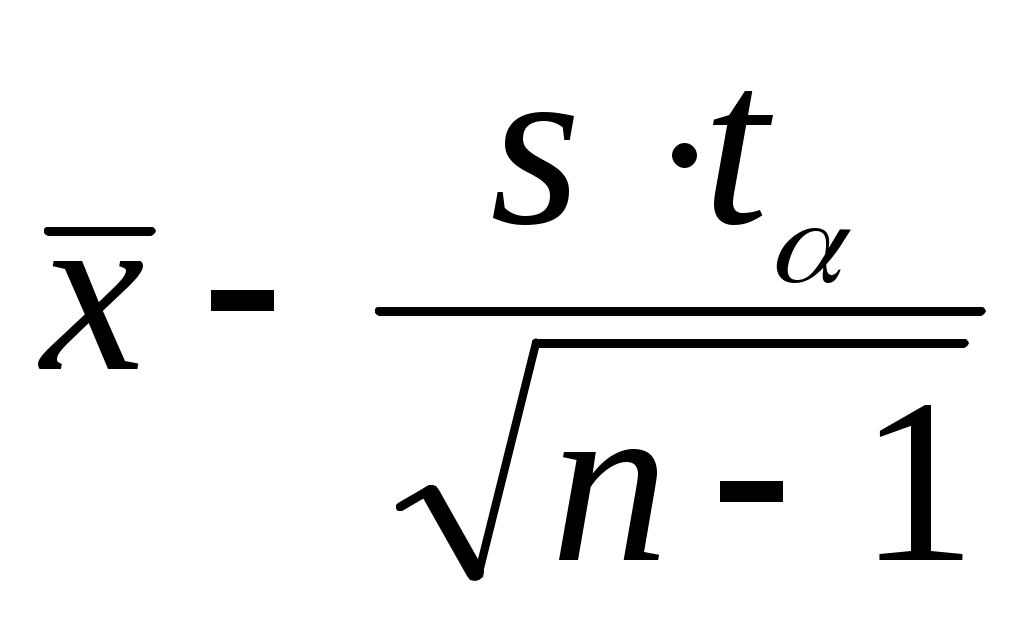= = 5,81,

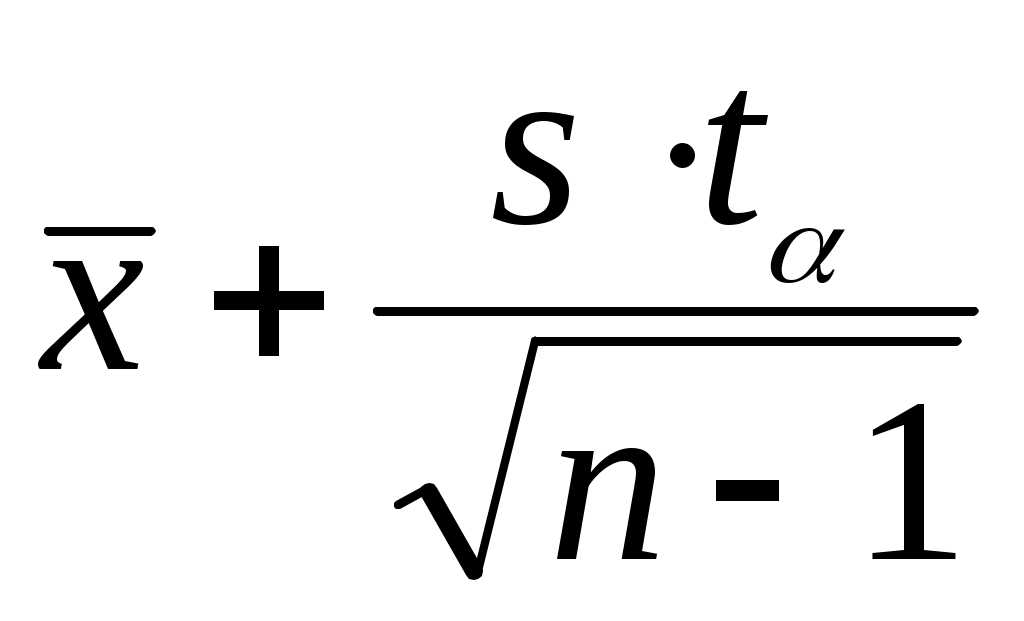= = 7,127.

Полученный доверительный интервал для математического ожидания:

= (5,81; 7,127).

Рассчитаем границы доверительного интервала для дисперсии.

Рассчитаем значения:

= 0,025 , = 0,975.

Из таблицы - распределения, по входам k=(n –1)=45 и =0,025, k=(n –-1) = 45 и =0,975 найдем значения критических точек и :

=28,366,

= 65,41.

Границы доверительного интервала рассчитаем по формулам:

= 3,382 ,

= 7,799.
Полученный доверительный интервал для дисперсии:

= (3,382; 7,799).

4.Построение интервального статистического ряда

Находим размах выборки:

r =х_max- x_min=11,054-2,661=8,393.

Находим количество разрядов (интервалов) q= 7, длину интервала делаем одинаковой:

---

l_i = r/q = 8,393/ 7 =1,2.

Выделяем представителей разрядов и подсчитываем число элементов выборки n_j, попавших в j-й разряд (интервал). Рассчитываем относительную частоту попадания элементов в разряды, т. е. относительные частоты разрядов p_j^* статистического ряда:

p_j^* = n_j / n , (j= ).

На основе относительных частот рассчитываем плотность относительной частоты для каждого разряда по формуле:

= , (j= ),

здесь – длина j-го разряда.

Интервальный статистический ряд представлен в Таблице 3.
Таблица 3

Номер интервала	1	2	3	4	5	6	7
Границы интервалов	2.661;3.861	3.861;5.061	5.061;6.261	6.261;7.461	7.461;8.661	8.661;9.861	9.861;11.061
Длина интервала	1.2	1.2	1.2	1.2	1.2	1.2	1.2
Частота интервала	6	8	11	4	8	6	3
Относительная частота интервалов	0.1304348	0.17391304	0.2391304	0.0869565	0.17391304	0.13043478	0.06521739
Плотность относительной частоты	0.1086957	0.14492754	0.1992754	0.0724638	0.14492754	0.10869565	0.05434783
Середина интервала	3.261	4.461	5.661	6.861	8.061	9.261	10.461

---