Файл: Правила проведения суммативного оценивания 5 Модерация и выставление баллов 6.docx

Типы заданий:

МВО – задания с множественным выбором ответов;

КО – задания, требующие краткого ответа;

РО – задания, требующие развернутого ответа.

Структура суммативного оценивания

Данный вариант состоит из 9 заданий, включающих вопросы с множественным выбором ответов, с кратким и развернутым ответами.

В вопросах с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов.

В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.

В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.

Характеристика заданий суммативного оценивания за 2 четверть

Раздел	Проверяемая цель	Уровень мыслительных навыков	Кол. заданий*	№ задания*	Тип задания*	Время на выполнение, мин*	Балл*	Балл за раздел
Преобразования плоскости	9.1.4.8 Знать виды, композиции движений и их свойства	Знание и понимание	5	1,2,3,4	МВО	6	4	20
	9.1.4.8 Знать виды, композиции движений и их свойства	Знание и понимание	5	5	КО	4	2
	9.1.4.9 Строить образы фигур при симметриях, параллельном переносе, повороте	Применение	1	6	КО	8	4
	9.1.4.12 Строить образы различных фигур при гомотетии	Применение	1	9	КО	6	2
	9.1.4.14 Знать и применять признаки подобия треугольников	Применение	1	8	РО	10	5
	9.1.4.16 Знать и применять свойство биссектрисы треугольника	Применение	1	7	КО	6	3
ИТОГО:			9			40		20
Примечание:-разделы,вкоторыеможновноситьизменения*

Образец заданий и схема выставления баллов Задания суммативного оценивания за 2 четверть

Какой из отрезков может быть образом отрезка АВпри движении?
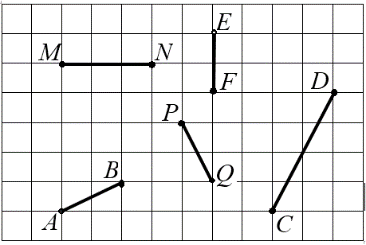1. МN
2. РQ
3. EF
4. DС

[1]

При каких значениях хи уточки А (x; 7) и В(–4; у)симметричны относительно начала координат?

A) х = – 4, у = –7 В) х = – 4, у = 7 C) х=4, у= –7

D) х= 4, у=7
[1]

Точка О— центр правильного восьмиугольника АВСDЕFКМ. Укажите образ стороны EF

при повороте вокруг точки Опо часовой стрелке на угол 135°.

А) AВ

ВС
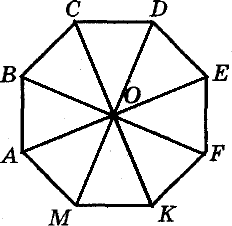СD
МA

[1]

Какая фигура имеет центр симметрии и ось симметрии?
1. равносторонний треугольник
2. параллелограмм
3. равнобокая трапеция
4. прямая

[1]

Параллельный перенос задан формулами:

^x^^^x^¹,

^y^^^y^⁵.

Найдите образ точки А(3; –4) при данном параллельном переносе.

[2]

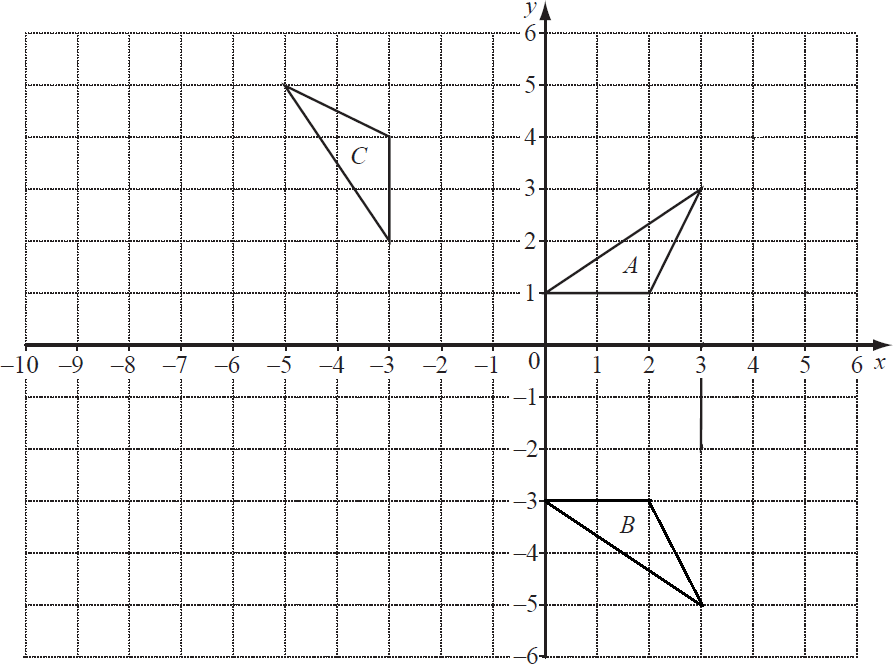На приведенном ниже рисунке показаны треугольники А, Ви С.

Поворот отображает треугольник Ав треугольник С. Найдите:
1. координаты центра этого поворота;
2. угол и направление этого поворота.

[2]

Опишите полностью преобразование, которое переводит треугольник Ав треугольник В.

[2]

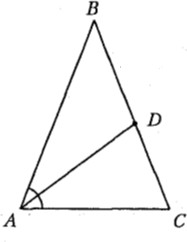В равнобедренном треугольнике АВС основание АС и боковая сторона АВ соответственно равны 5 см и 10 см. Биссектриса AD угла А при основании треугольника делит сторону ВС на отрезки ВDи DС. Найдите длины этих отрезков.

[3]

Диагонали трапеции ABCDпересекаются в точке О. Точка пересечения диагоналей трапеции делит диагональ AC на отрезки длиной 11 см и 7 см. Найдите основания трапеции ADи ВС, если их разность равна 16 см. Выполните чертеж по условию задачи.

[5]

Постройте трапецию, гомотетичную данной, с центром в точке (–3;0) и коэффициентом

1

равным ₃.

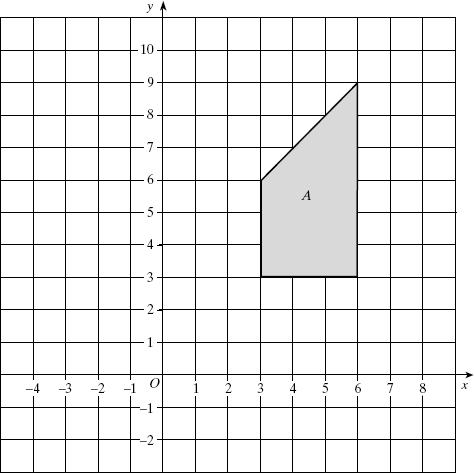
[2]

Схема выставления баллов

№	Ответ	Балл	Дополнительная информация
1	B	1
2	С	1
3	D	1
4	D	1
5	x'=3-1=2	1
5	y'=-4+5=1	1
6a	(–2; 0)	1
6a	Поворот на 90° против часовой стрелки или положительное направление	1	Принимается альтернативный ответ
6b	Симметрия относительно прямой	1
6b	^Прямаяy 1	1
7	DC х, ^BD^¹⁰^^х x_10  x 5 10	1	Использует свойство биссектрисы треугольника
	DC 3 ¹см 3	1
	BD 6 ²см 3	1
8	Выполнен чертеж по условию задачи	1
	^{Доказано} BOС DOA^(по^двум^углам)	1
	11 _x 16 7 x	1
	x 28	1
	BC= 28 см, AD = 44 см	1
9		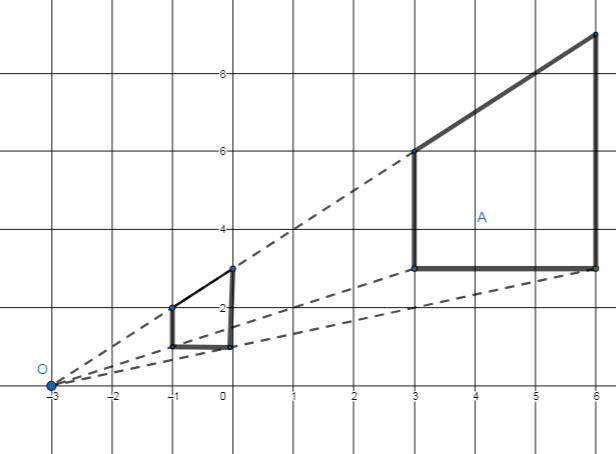1	Использован коэффициент гомотетии
9		1	Построена гомотетичная фигура
Итого:		20