Файл: Правила проведения суммативного оценивания 5 Модерация и выставление баллов 6.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 170
Скачиваний: 1
СОДЕРЖАНИЕ
Правила проведения суммативного оценивания
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 1 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 2 четверть
1 равным 3 . [2] Схема выставления баллов
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Структура суммативного оценивания
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 4 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
МВО – задания с множественным выбором ответов;
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 6 заданий, включающих вопросы с множественным выбором ответов, с кратким и развернутым ответами.
В вопросах с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
Характеристика заданий суммативного оценивания за 4 четверть
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задания* | Время на выполнение, мин* | Балл* | Балл за раздел |
| Окружность. Многоугольники | 9.1.2.2 Знать определение и свойства правильных многоугольников | Знание и понимание | 1 | 1 | МВО | 2 | 1 | 20 |
| 9.1.1.1 Выводить и применять формулу длины дуги | Применение | 1 | 2 | МВО | 2 | 1 | ||
| 9.1.2.1 Знать и применять свойства и признаки вписанных и описанных четырёхугольников | Применение | 1 | 3 | КО | 6 | 4 | ||
| 9.1.2.5 Знать и применять формулы, связывающие стороны, периметр, площадь правильного многоугольника и радиусы вписанной и описанной окружностей правильного многоугольника | Применение | 1 | 4 | РО | 8 | 4 | ||
| 9.1.2.6 Знать и применять свойства медиан треугольника | Применение | 1 | 5 | РО | 10 | 5 | ||
| 9.1.1.2 Выводить и применять формулу площади сектора, сегмента | Применение | 1 | 6 | РО | 12 | 5 | ||
| ИТОГО: | | | 6 | | | 40 | 20 | 20 |
| Примечание:*-разделы,вкоторыеможновноситьизменения | ||||||||
Образец заданий и схема выставления баллов Задания суммативного оценивания за 4 четверть
-
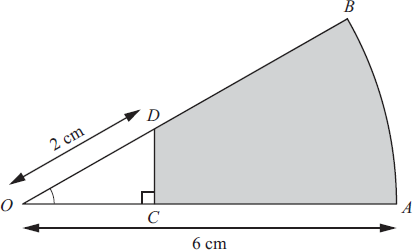
Найдите количество сторон правильного многоугольника, если сумма всех его внутренних углов равна 1440°.
А) 8
В) 9
С) 10
D) 12
[1]
-
Дана окружность радиуса 12 см . Чему равна длина ее дуги с градусной мерой 60°?
А) 4 см
В) 6 см
С) 8 см
D) 12 см
[1]
-
Три угла четырехугольника, вписанного в окружность, взятые в порядке следования, относятся как 2 : 6 : 7. Найдите углы четырехугольника.
[4]
-
В окружность вписан квадрат со стороной треугольника, описанного около этой окружности.
-
см. Найдите площадь правильного
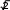 [4]
[4]-
Основание АВтреугольника АВСравно 26 см. Медианы АКи ВМ, проведенные к боковым сторонам, равны соответственно 30 см и 39 см. Найдите площадь треугольника АВС.
[5]
-
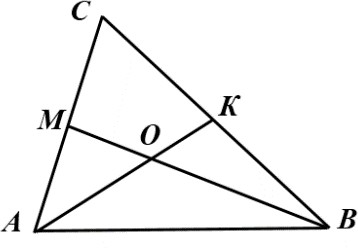
На рисунке изображен сектор круга с центром в точке Oи радиусом, равным 6 см.
 ОD=2 сми DOС 45°. Найдите площадь закрашенной области.
ОD=2 сми DOС 45°. Найдите площадь закрашенной области.[5]
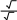
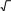
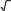
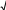
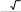

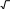

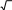
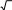
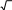 Схема выставления баллов
Схема выставления баллов | № | Ответ | Балл | Дополнительная информация |
| 1 | С | 1 | |
| 2 | А | 1 | |
| 3 | 2х+ 7х= 180° | 1 | |
| х= 20° | 1 | | |
| 40°, 120°, 140° | 1 | | |
| 180° – 120° = 60° | 1 | | |
| | R a 4 2 4 см | 1 | |
| | 2 2 | ||
| 4 | ra, 4 a 2 3 2 3 | 1 | Принимается альтернативное решение |
| | a 8 3 см | 1 | |
| | a2 3 8 32 3 S 48 3 см2 4 4 | 1 | |
| 5 | АО=2х,ОК=х 2х х 30 или ВО=2х,ОМ=х 2х х 39 | 1 | Применяет свойство медиан треугольника |
| АО= 20 см и ВО = 26 см | 1 | | |
| 20 26 26 Полупериметр р 36 см2 | 1 | | |
| S 36(36 20)(36 26)(36 26) 240 см2 AOB | 1 | | |
| S 3 240 720 см2 ABC | 1 | Применяет свойство медиан треугольника | |
| | r2 62 | 1 | |
| | Sсектора 360∘ 360° 45° 4,5 | ||
| | DC DOsin 45° | | Принимается |
| | 1 | альтернативное | |
| 6 | | решение | |
| DC 2 | 1 | | |
| | S 1 2 2 1 | 1 | |
| | 2 | ||
| | Sфигуры 4,5 1 | 1 | |
| Итого: | 20 | | |