Файл: Правила проведения суммативного оценивания 5 Модерация и выставление баллов 6.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 168
Скачиваний: 1
СОДЕРЖАНИЕ
Правила проведения суммативного оценивания
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 1 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 2 четверть
1 равным 3 . [2] Схема выставления баллов
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Структура суммативного оценивания
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 4 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 6 заданий, включающих вопросы с кратким и развернутым ответами.
В вопросах, требующих краткого ответа, обучащийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/ вопросов.
 Характеристика заданий суммативного оценивания за 3 четверть
Характеристика заданий суммативного оценивания за 3 четверть | Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задания* | Время на выполнение, мин* | Балл* | Балл за раздел |
| Решение треугольников | 9.1.3.8 Знать и применять формулы площади вписанного треугольника (S = abc , где a, b, c- 4R стороны треугольника, R-радиус описанной окружности), площади описанного многоугольника (S = p ∙ r, где r – радиус вписанной окружности, p - полупериметр многоугольника) | Применение | 1 | 1 | КО | 3 | 2 | 20 |
| 9.1.3.7 Знать и применять теорему синусов | Применение | 1 | 3 | КО | 4 | 2 | ||
| 9.1.3.6 Знать и применять теорему косинусов | Применение | 1 | 2 | КО | 6 | 3 | ||
| 9.1.3.9 Знать и применять формулы для нахождения радиуса окружности, используя площади вписанных и описанных треугольников | Применение | 1 | 4 | РО | 7 | 6 | ||
| 9.1.3.10 Применять теоремы синусов и косинусов для решения треугольников и прикладных задач | Навыки высокого порядка | 2 | 5 | РО | 10 | 3 | ||
| 6 | РО | 10 | 4 | |||||
| ИТОГО: | | | 6 | | | 40 | 20 | 20 |
| Примечание:*-разделы,вкоторыеможновноситьизменения | ||||||||
Образец заданий и схема выставления баллов Задания суммативного оценивания за 3 четверть
-
Радиус окружности, вписанной в треугольник, равен 3, а периметр треугольника – 20. Найдите площадь треугольника.
[2]
-
Не вычисляя углов треугольника, определите его вид (по величине углов), если стороны треугольника равны:
а) 2, 3 и 4; b) 6,10 и 11; с) 8, 15 и 17.
[3]
-
В треугольнике АВСизвестно, что АВ= 12 см, ВС= 10 см, sin A= 0,2. Найдите синус угла С треугольника.
[2]
-
Основания равнобокой трапеции ABCDравны 9 см и 21 см, а высота – 8 см. Найдите:-
диагональ трапеции АС; -
радиус окружности, описанной около трапеции.
-
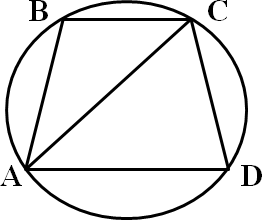
[6]
-
Определите ширину реки ABдля геодезических измерений как показано на рисунке:
В1050 ,
С 450 ,
ВС 250 м.
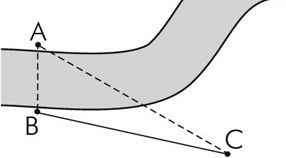
[3]
-
К одной точке приложили две силы: F1 = 10 H и F2= 20 H под углом 60°. Найдите равнодействующую этих двух сил. Выполните рисунок.
[4]
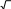 Схема выставления баллов
Схема выставления баллов | № | Ответ | Балл | Дополнительная информация | ||
| 1 | Полупериметр р = 10 см и использована формула r S p | 1 | | ||
| S 10 3 30 см | 1 | | |||
| 2 | 42 22 32 тупоугольный треугольник | 1 | Определяет знак косинуса угла | ||
| 112 102 62 остроугольный треугольник | 1 | Определяет знак косинуса угла | |||
| 172 152 82 прямоугольный треугольник | 1 | | |||
| 3 | 12 10 sin С 0,2 | 1 | | ||
| sin С= 0,24 | 1 | | |||
| 4 | Применяет теорему Пифагора | 1 | Принимается альтернативное решение | ||
| AB= CD= 10 см | 1 | ||||
| АС= 17 см | 1 | ||||
| S 1 8 21 84 см2 ACD 2 | 1 | ||||
| Использована формула R abc 172110 4S 4 84 | 1 | ||||
| R 85 10 5 см 8 8 | 1 | ||||
| 5 | А 300 | 1 | | ||
| 250 AB , 250 AB sin 300 sin 450 1 2 2 2 | 1 | | |||
| AB 250 2 м | 1 | | |||
| 6 | Рисунок соответствует условию задачи | 1 | | ||
| Второй угол построенного параллелограмма 120° | 1 | | |||
| F2 102 202 2 10 20 cos1200 | 1 | | |||
| F10 7H | 1 | | |||
| Итого: | 20 | | |||