Файл: Правила проведения суммативного оценивания 5 Модерация и выставление баллов 6.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 171
Скачиваний: 1
СОДЕРЖАНИЕ
Правила проведения суммативного оценивания
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 1 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 2 четверть
1 равным 3 . [2] Схема выставления баллов
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Структура суммативного оценивания
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 4 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 1 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 6 заданий, включающих вопросы с кратким и развернутым ответами.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
Характеристика заданий суммативного оценивания за 1 четверть
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задания* | Время на выполнение, мин* | Балл* | Балл за раздел |
| Векторы на плоскости | 9.1.4.5 Знать определение угла между двумя векторами | Знание и понимание | 1 | 1 | КО | 2 | 2 | 20 |
| 9.1.4.4 Раскладывать вектор по двум неколлинеарным векторам | Применение | 1 | 2 | РО | 5 | 2 | ||
| 9.1.4.2 Знать и применять правила сложения векторов и умножения вектора на число | Применение | 1 | 3 | КО | 3 | 2 | ||
| 9.1.3.3 Выполнять действия над векторами в координатах | Применение | 1 | 4 | РО | 5 | 3 | ||
| 9.1.3.4 Знать и применять скалярное произведение векторов и его свойства | Применение | 1 | 5 | РО | 10 | 5 | ||
| 9.1.4.7 Решать задачи векторным методом | Навыки высокого порядка | 1 | 6 | РО | 15 | 6 | ||
| ИТОГО: | | | 6 | | | 40 | 20 | 20 |
| Примечание:*-разделы,вкоторыеможновноситьизменения | ||||||||
Образец заданий и схема выставления баллов Задания суммативного оценивания за 1 четверть
-

 Четырехугольник АВСD– ромб. Диагональ ВDравна стороне ромба. Найдите угол между векторами ВАи АD.
Четырехугольник АВСD– ромб. Диагональ ВDравна стороне ромба. Найдите угол между векторами ВАи АD.
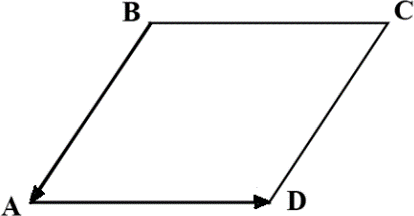
[2]
-
Точка Млежит на стороне ВСпараллелограмма АВСD, причем ВМ:МС= 3:1. Выразите



вектор АМчерез векторы
ВС а→
и ВА → .
b
[2]
-


 Четырехугольник АВСD– параллелограмм. Найдите
Четырехугольник АВСD– параллелограмм. Найдите
BА BC AD.
[2]
-
b
Найдите модуль вектора m→ 1 a→ 2 →
2
 , где
, гдеа 2i→ 4 →j
→
→ →
и b 3i 5 j.
[3]
5. Даны векторы m→ (4;3) , n→ (5;12) , a→ (2; x) . Найдите:
-
косинус угла между векторами m→ и n→ ; -
число x, если векторы m→ и a→ коллинеарны;
с) число x, если векторы n→ и a→ перпендикулярны.
[5]
 6. Решите задачу векторным методом. Выполните рисунок.
6. Решите задачу векторным методом. Выполните рисунок.Дан треугольник АВС. Известно, что АВ= 4 см, Найдите длину медианы ВМ.
ВС 6
-
см,
АВС 300 .
[6]

























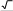 Схема выставления баллов
Схема выставления баллов | № | Ответ | Балл | Дополнительная информация |
| 1 | Углы ромба 60° и 120° | 1 | |
| ВА, AD 120∘ | 1 | | |
| 2 | AM AB BM, АВ bилиBM 3 a 4 | 1 | Принимается альтернативное решение |
| AM 3 a b 4 | 1 | | |
| 3 |    ВА ВС СА | 1 | Принимается альтернативное решение |
   CА AD СD | 1 | | |
| 4 | 1 2i→ 4 →j 23i→ 5 →j 2 | 1 | |
| m→ 5i→ 12 →j | 1 | | |
| m→ 13 | 1 | | |
| 5 | а) m→ 5 , n→ 13 | 1 | |
| m→ n→ 16 | 1 | | |
| cos(m,n) 16 65 | 1 | | |
| b) 4 3 х 3 2 х 2 | 1 | | |
| c) 5 2 12х 0 х 5 6 | 1 | | |
| | Выполнен рисунок по условию задачи | 1 | |
| | BM 1 BA BC | 1 | |
| | 2 | ||
| | BM2 1 BA BC2 1 BA2 2BA BC BC2 | 1 | Принимается альтернативное решение |
| | 4 4 | ||
| 6 | BM2 1 BA BC2 1 BA2 2 BA BC cos ABC BC2 4 4 | 1 | |
| | 2 1 3 BM 16 48 3 108 49 4 2 | 1 | |
| | BM 7 | 1 | |
| Итого: | 20 | | |