Файл: Таырып Доалатарды рельстерге ілінісу, ілінісу коэффициенті.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 269
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Тақырып Доңғалақтарды рельстерге ілінісу, ілінісу коэффициенті.
Пайдалану шарттары бойынша қарсылық күштерін жіктеу:
Дөңгелектердің рельстердегі үйкеліс сырғанау кедергісі
Рис. Доңғалақ жұбының А ұзындығындағы жолдың біркелкі простігін өтуі'.
6. Энергияның қоршаған ортаға таралу.
Методы экспериментального определения основного сопротивления движению.
Тема 5. Дополнительные силы сопротивления движению.
Тема 6. Добавочное сопротивление при трогании поезда с места.
ОБЩЕЕ СОПРОТИВЛЕНИЕ ДВИЖЕНИЮ ПОЕЗДА.
= (Р+Q) cosaμ·103 (2)
Wi — дополнительное сопротивление от уклона профиля пути, Н:
Wi = (Р+Q) sina• 103. (3)
Разделим все члены уравнения (1) на вес поезда (Р + Q) и определим удельное общее сопротивление движению поезда по подъему, Н/кН:
wK = w0 + wi (4)
где w0 — основное удельное сопротивление движению поезда, Н/кН;
wi — дополнительное удельное сопротивление от уклона профиля пути, Н/кН:
wi = 1000 sina (5)
При движении поезда по уклону любого знака, Н/кН:
wK = w0 ± wi (6)
знаки « + » — подъем, « - » — спуск.
Как отмечалось ранее (см. раздел 1.2), величина крутизны уклона профиля пути i по определению равна синусу угла а, увеличенному в 1000 раз, ‰, т.е.
i=1000 sina (7)
Сравнение уравнений (5) и (7) позволяет сделать вывод, что каждая тысячная уклона действует на поезд с силой в 1Н на каждый кН его веса, т.е.
1‰ - 1 Н/кН.
Многочисленными экспериментами было установлено, что в реальных условиях эксплуатации величина удельного сопротивления от уклона профиля пути wi меньше крутизны уклона i, т.е. wi < i. Это объясняется тем, что на спусках (-i) поезд сжат и увеличивается виляние вагонов; при движении по подъему (+i) поезд растянут и виляние вагонов уменьшается.
В среднем для вагонов, оборудованных автосцепками, Н/кН:
wi ≈ ±0,9i
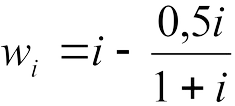
Известный русский ученый тяговик, создатель «Конторы опытов над паровозами» (ВНИИЖТ) проф. Ю.В. Ломоносов 1915 г. предложил следующую формулу для расчета удельного сопротивления движению ПС от уклона профиля пути, Н/кН:
где i— крутизна уклона, ‰.
В настоящее время при выполнении тяговых расчетов погрешностью 5— 10 % между величинами wi и i пренебрегают и считают
wi = I
Максимально возможная крутизна подъема, которую может преодолеть локомотив с составом, в основном, зависит от веса поезда и условий сцепления колес локомотива с рельсами.
От кривизны пути. Дополнительное сопротивление ПС в кривых участках пути возникает по следующим основным причинам.
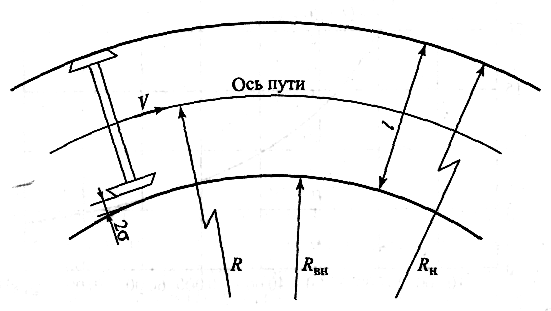
Рис. Движение колесной пары в кривой радиусом R
При выполнении тяговых расчетов принимают, что колпары ПС проходят путь Sпо кривой радиусом R, т.е. по средней линии (оси) пути (рис.), м:
S=2πR (1)
Однако левое колесо колпары движется по радиусу наружного рельса RН, который больше R, м:
RH = R+ l/2
где l—ширина колеи, м.
Правое колесо колпары - по внутреннему рельсу радиусом RBH, м:
RВН = R- l/2
Из формулы (1) следует, что разница в радиусах наружного и внутреннего рельсов должна приводить к тому, что путь, проходимый колесом по
наружному рельсу, будет больше, чем по внутреннему рельсу. Конусность бандажей колпары уменьшает эту разницу в радиусах RН и RBH, тем не менее, при движении экипажей по кривой всегда возникает проскальзывание колес, вызывающее появление дополнительных сил трения скольжения.
Из-за сложности учета всех факторов, действующих на экипаж ПС в кривых, во многих странах мира обычно пользуются эмпирическими формулами, учитывающими основной фактор — радиус кривизны пути R.
При расчете величины удельного сопротивления от кривизны пути обычно применяют два вида формул, Н/кН:
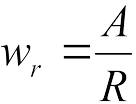 и
и 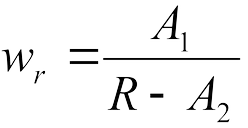
где A, A1, А2 — эмпирические коэффициенты; R—радиус кривой, м.
На железных дорогах РФ и РК удельное сопротивление от кривизны пути для всех видов ПС определяется по следующей эмпирической формуле при А= 700, Н/кН:
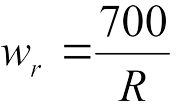 (2)
(2)
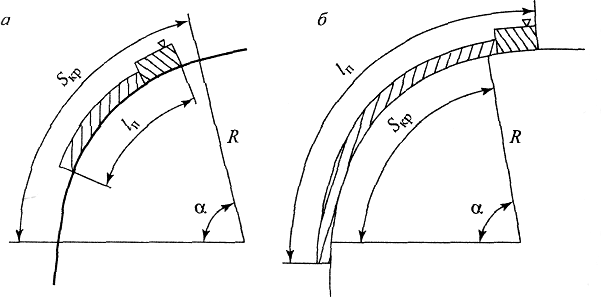
Рис. Схемы прохождения поездом длиной lп кривых участков пути
В том случае, если кривая задана не радиусом R, а центральным углом а(в градусах) и длиной кривой Sкр (рис.), формулу (2) преобразуют. Так как окружность имеет центральный угол а = 360°, a ее длина S=2πR, то длина кривой Sкр, м, с центральным углом а° будет равна:
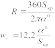
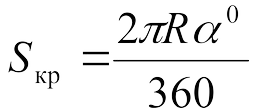 откуда подставив в формулу (2) (3)
откуда подставив в формулу (2) (3)
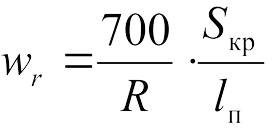 Необходимо отметить, что применение формул (2) и (3) возможно при условии, что весь поезд размещается в кривой, т.е. длина поезда lп меньше или равна длине кривой Sкр (рис. а). Если длина поезда превышает длину кривой (рис. б), то дополнительное сопротивление движению wr будет испытывать та часть поезда, которая находится в кривой. В этом случае в формулы (2) и (3) вводится поправка Sкр / lп, например, формула (2) примет вид, Н/кН:
Необходимо отметить, что применение формул (2) и (3) возможно при условии, что весь поезд размещается в кривой, т.е. длина поезда lп меньше или равна длине кривой Sкр (рис. а). Если длина поезда превышает длину кривой (рис. б), то дополнительное сопротивление движению wr будет испытывать та часть поезда, которая находится в кривой. В этом случае в формулы (2) и (3) вводится поправка Sкр / lп, например, формула (2) примет вид, Н/кН:
Если кривая совпадает с уклоном профиля пути, то определяют суммарный приведенный уклон, ‰:
iс = wr ± i
Знак « + » соответствует подъему; « - » — спуску.
С ростом скорости (дополнительное удельное сопротивление wr сначала снижается, затем вновь возрастает. Минимальные значения величины wr наблюдаются в диапазоне скоростей 60—70 км/ч у грузовых вагонов и 40—50 км/ ч у локомотивов. Объясняется это заметным влиянием на величину удельного сопротивления от кривизны пути абсолютного непогашенного ускорения т в кривой, м/с2:
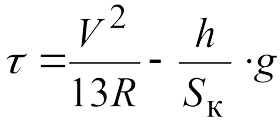 (4)
(4)
где h— возвышение наружного рельса, мм;
Sк — расстояние между кругами катания колес ПС, Sк = 1600 мм; g— ускор. свободного падения, g= 9,81 м/с2.
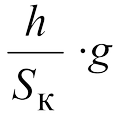 Из формулы (4) следует, что величина непогашенного ускорения экипажа в кривой τпредставляет разницу между центробежным ускорением V2/13Rи ускорением, которое создает горизонтальная составляющая веса вагона
Из формулы (4) следует, что величина непогашенного ускорения экипажа в кривой τпредставляет разницу между центробежным ускорением V2/13Rи ускорением, которое создает горизонтальная составляющая веса вагона
.
На рис. показана схема сил, действующих на вагон весом q, при прохождении кривой. Для уравновешивания центробежной силы наружному рельсу кривой придают возвышение hнад внутренним рельсом, что создает горизонтальную составляющую веса вагона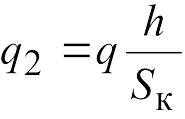 , направленную в сторону, противоположную действию центробежной силы.
, направленную в сторону, противоположную действию центробежной силы.
При τ = 0, когда центробежная сила и горизонтальная составляющая веса вагона равны, удельное сопротивление от кривизны пути минимальное (диапазон скоростей V = 60—70 км/ч). При высоких скоростях движения более 70 км/ч центробежное ускорение превышает величину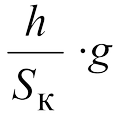 и величина τ положительна, центробежная сила прижимает гребни бандажей к внутренней боковой грани наружного рельса. Чем выше скорость движения, тем сильнее прижатие гребней к рельсу и дополнительное сопротивление от кривизны пути заметно увеличивается. В диапазоне скоростей 20—60 км/ч величина τ отрицательная, под
и величина τ положительна, центробежная сила прижимает гребни бандажей к внутренней боковой грани наружного рельса. Чем выше скорость движения, тем сильнее прижатие гребней к рельсу и дополнительное сопротивление от кривизны пути заметно увеличивается. В диапазоне скоростей 20—60 км/ч величина τ отрицательная, под
Wi — дополнительное сопротивление от уклона профиля пути, Н:
Wi = (Р+Q) sina• 103. (3)
Разделим все члены уравнения (1) на вес поезда (Р + Q) и определим удельное общее сопротивление движению поезда по подъему, Н/кН:
wK = w0 + wi (4)
где w0 — основное удельное сопротивление движению поезда, Н/кН;
wi — дополнительное удельное сопротивление от уклона профиля пути, Н/кН:
wi = 1000 sina (5)
При движении поезда по уклону любого знака, Н/кН:
wK = w0 ± wi (6)
знаки « + » — подъем, « - » — спуск.
Как отмечалось ранее (см. раздел 1.2), величина крутизны уклона профиля пути i по определению равна синусу угла а, увеличенному в 1000 раз, ‰, т.е.
i=1000 sina (7)
Сравнение уравнений (5) и (7) позволяет сделать вывод, что каждая тысячная уклона действует на поезд с силой в 1Н на каждый кН его веса, т.е.
1‰ - 1 Н/кН.
Многочисленными экспериментами было установлено, что в реальных условиях эксплуатации величина удельного сопротивления от уклона профиля пути wi меньше крутизны уклона i, т.е. wi < i. Это объясняется тем, что на спусках (-i) поезд сжат и увеличивается виляние вагонов; при движении по подъему (+i) поезд растянут и виляние вагонов уменьшается.
В среднем для вагонов, оборудованных автосцепками, Н/кН:
wi ≈ ±0,9i
Известный русский ученый тяговик, создатель «Конторы опытов над паровозами» (ВНИИЖТ) проф. Ю.В. Ломоносов 1915 г. предложил следующую формулу для расчета удельного сопротивления движению ПС от уклона профиля пути, Н/кН:
где i— крутизна уклона, ‰.
В настоящее время при выполнении тяговых расчетов погрешностью 5— 10 % между величинами wi и i пренебрегают и считают
wi = I
Максимально возможная крутизна подъема, которую может преодолеть локомотив с составом, в основном, зависит от веса поезда и условий сцепления колес локомотива с рельсами.
От кривизны пути. Дополнительное сопротивление ПС в кривых участках пути возникает по следующим основным причинам.
-
Колеса одной колпары проходят разный путь по наружному и внутреннему рельсам, что приводит к увеличению проскальзывания колес и дополнительным потерям энергии поезда.

Рис. Движение колесной пары в кривой радиусом R
При выполнении тяговых расчетов принимают, что колпары ПС проходят путь Sпо кривой радиусом R, т.е. по средней линии (оси) пути (рис.), м:
S=2πR (1)
Однако левое колесо колпары движется по радиусу наружного рельса RН, который больше R, м:
RH = R+ l/2
где l—ширина колеи, м.
Правое колесо колпары - по внутреннему рельсу радиусом RBH, м:
RВН = R- l/2
Из формулы (1) следует, что разница в радиусах наружного и внутреннего рельсов должна приводить к тому, что путь, проходимый колесом по
наружному рельсу, будет больше, чем по внутреннему рельсу. Конусность бандажей колпары уменьшает эту разницу в радиусах RН и RBH, тем не менее, при движении экипажей по кривой всегда возникает проскальзывание колес, вызывающее появление дополнительных сил трения скольжения.
-
За счет действия центробежных сил (MV2)/R в кривой гребни колес прижимаются к внутренней боковой грани наружного рельса, в результате возникают силы бокового трения скольжения. При увеличении радиуса кривой величина центробежных сил уменьшается, соответственно, снижается дополнительное сопротивление от кривизны пути. -
Тележки ПС (локомотива и вагонов) поворачиваются относительно оси кузова. В опорах, шкворневых устройствах и буксах возрастают силы трения скольжения.
Из-за сложности учета всех факторов, действующих на экипаж ПС в кривых, во многих странах мира обычно пользуются эмпирическими формулами, учитывающими основной фактор — радиус кривизны пути R.
При расчете величины удельного сопротивления от кривизны пути обычно применяют два вида формул, Н/кН:
где A, A1, А2 — эмпирические коэффициенты; R—радиус кривой, м.
На железных дорогах РФ и РК удельное сопротивление от кривизны пути для всех видов ПС определяется по следующей эмпирической формуле при А= 700, Н/кН:

Рис. Схемы прохождения поездом длиной lп кривых участков пути
В том случае, если кривая задана не радиусом R, а центральным углом а(в градусах) и длиной кривой Sкр (рис.), формулу (2) преобразуют. Так как окружность имеет центральный угол а = 360°, a ее длина S=2πR, то длина кривой Sкр, м, с центральным углом а° будет равна:
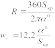
Если кривая совпадает с уклоном профиля пути, то определяют суммарный приведенный уклон, ‰:
iс = wr ± i
Знак « + » соответствует подъему; « - » — спуску.
С ростом скорости (дополнительное удельное сопротивление wr сначала снижается, затем вновь возрастает. Минимальные значения величины wr наблюдаются в диапазоне скоростей 60—70 км/ч у грузовых вагонов и 40—50 км/ ч у локомотивов. Объясняется это заметным влиянием на величину удельного сопротивления от кривизны пути абсолютного непогашенного ускорения т в кривой, м/с2:
где h— возвышение наружного рельса, мм;
Sк — расстояние между кругами катания колес ПС, Sк = 1600 мм; g— ускор. свободного падения, g= 9,81 м/с2.
.
На рис. показана схема сил, действующих на вагон весом q, при прохождении кривой. Для уравновешивания центробежной силы наружному рельсу кривой придают возвышение hнад внутренним рельсом, что создает горизонтальную составляющую веса вагона
При τ = 0, когда центробежная сила и горизонтальная составляющая веса вагона равны, удельное сопротивление от кривизны пути минимальное (диапазон скоростей V = 60—70 км/ч). При высоких скоростях движения более 70 км/ч центробежное ускорение превышает величину