ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 248
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
задачи. Ценность задач подобного рода состоит в том, что при их решении учащиеся обнаруживают общие видовые сходства и отличия. Таким образом, получаем, что:


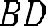

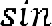
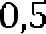



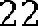

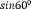

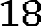




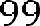


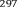
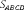
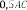
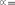
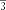
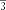
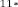 .
.

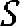
 Поскольку по условию задачи с одной стороны площадь правильного треугольника со стороной х равна площади трапеции, а с другой стороны вычисляется по формуле
Поскольку по условию задачи с одной стороны площадь правильного треугольника со стороной х равна площади трапеции, а с другой стороны вычисляется по формуле 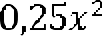 , то получаем уравнение
, то получаем уравнение

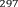


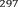







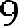
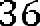

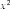
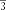


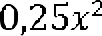 или . Так как 297=9*3*11, то наше уравнение принимает вид или .
или . Так как 297=9*3*11, то наше уравнение принимает вид или .







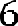
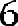


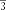
 Откуда следует, что . Ответ: .
Откуда следует, что . Ответ: .
В качестве домашнего задания можно предложить учащимся следующие
задачи.
ВС= 15 см.
Выводы по второй главе.
«Площадь многоугольника».
Сформулируем основные выводы и полученные результаты проведенного исследования.
планиметрических задач.
«Вписанные и описанные многоугольники» .
3. С. 56-62.
С.2-9.
классы: пособие для учителей общеобразоват. организаций/ составитель Т.А. Бурмистрова. – М.: Просвещение, 2011. – 95 с.
«Математическое просвещение», выпуск 16, (2002).






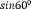







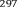
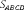
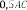
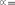
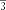
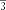
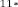 .
.
 Поскольку по условию задачи с одной стороны площадь правильного треугольника со стороной х равна площади трапеции, а с другой стороны вычисляется по формуле
Поскольку по условию задачи с одной стороны площадь правильного треугольника со стороной х равна площади трапеции, а с другой стороны вычисляется по формуле 
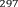


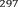








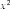
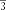











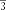
 Откуда следует, что . Ответ: .
Откуда следует, что . Ответ: .В качестве домашнего задания можно предложить учащимся следующие
задачи.
-
Найти сторону квадрата, зная, что его площадь численно равна площади ромба ABCD с диагоналями AC=24 см и BD=0,36 м. -
Найти сторону правильного треугольника, зная, что его площадь численно равна площади прямоугольника ABCD со сторонами АВ=27 см,
ВС= 15 см.
-
 Найти площадь квадрата, зная, что его сторона равна стороне правильного треугольника с высотой .
Найти площадь квадрата, зная, что его сторона равна стороне правильного треугольника с высотой .
Выводы по второй главе.
-
Раскрыты формы, методы и средства обучения по решению планиметрических задач. -
Рассмотрены методические рекомендации по обучению темы
«Площадь многоугольника».
-
Разработана система задач ОГЭ по теме «Площадь многоугольника».
ЗАКЛЮЧЕНИЕ
Сформулируем основные выводы и полученные результаты проведенного исследования.
-
Рассмотрено понятие логико-математического анализа тем школьного курса математики на примере содержания темы «Площадь многоугольника». Выявлено, что материал по данной теме организован на дедуктивной основе, так как всем фигурам, вводимым в теме, даются определения. -
Выявлено, что в методической литературе понятие площадиопределяют как величинучасти плоскости, которая заключена внутри плоской замкнутой фигуры; через площадь фигуры - как частьплоскости, занимаемой этой фигурой. -
Представлен сравнительный анализ особенностей школьных учебников разных авторов по теме «Площадь многоугольника». -
Раскрыты формы, методы и средства обучения решения
планиметрических задач.
-
Рассмотрены методические рекомендации по обучению темы
«Вписанные и описанные многоугольники» .
-
Разработана анализ системы задач ОГЭ по данной теме.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
-
Александров, А.Д. О геометрии. // Математика в школе. 1980. №
3. С. 56-62.
-
Атанасян, Л.С. Геометрия: Доп. Главы к шк. Учеб. 8кл.: Учеб. пособие для учащихся шк. Классов с углубленным изучением математики / Л. С. Атанасян, В.Ф. Бутузова, C.Б. Кадомцев и др.- М.: Просвещение, 2005. -205 c.
-
Атанасян, Л.С. Изучение геометрии в 7 – 9 классах [Текст]: пособие для учителей / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др. – 7-е изд. – М.: Просвещение, 2009. – 255 с. -
Бескин, Н.М. Методика геометрии [Текст]: учебник для педагогиче- ских институтов / Н.М. Бескин. – М.: Учпедгиз, 1947. – 276 с. -
Болтянский, В.Г. О понятиях площади и объема. //Квант. 1977. №5.
С.2-9.
-
Бурмистрова, Т.А. Геометрия. Сборник рабочих программ. 7 – 9
классы: пособие для учителей общеобразоват. организаций/ составитель Т.А. Бурмистрова. – М.: Просвещение, 2011. – 95 с.
-
Вавилов В. В., Устинов А. В. Многоугольники на решетках. — М.: МЦНМО, 2006. — 72 с. -
Гейдман, Б.П., Площади многоугольников, Библиотека
«Математическое просвещение», выпуск 16, (2002).
-
Глаголев, Н.А. Элементарная геометрия. Планиметрия. Для 6-8 клас- сов семилетней и средней школы [Текст] / Н.А. Глаголев. – Ч.1. – М.: Учпед- гиз, 1954. – 236 с. -
Гусев, В.А. Методика обучения геометрии: учеб. пособие для студ. высш. пед. учеб. заведений [Текст] / В.А. Гусев, В.В. Орлов, В.А. Панчищина и др.; под ред. В.А. Гусева. – М.: Издат. центр «Академия», 2004. – 368 с. -
Евсеевичева, А.Н. [Электронный ресурс]. Геометрия. Тригонометрия./ Режим доступа: https://www.litres.ru/raznoe/geometriya- trigonometriya-matematika-eto-legko/ . Последнее обновление: 15.06.2018. -
Карасев, Р.Н. Математическое просвещение. Третья серия, выпуск 21, С.228.
-
Колягин, Ю.М. Методика преподавания математики в средней шко- ле. Общая методика [Текст]: учеб. пособие для студентов физ.-мат. фак. пед. Институтов / Ю.М. Колягин. – М.: Просвещение, 1975. – 462 с. -
Кольман, Э. История математики в древности / Э. Кольман. – М.: Физматлит, 1961. – 236 с. -
Лихачев Б.Т.. Педагогика: Курс лекций [Текст]: учеб. пособие для студентов педагог, учеб. заведений и слушателей ИПК и ФПК. — 4-е изд., перераб. и доп. — М.: Юрайт-М.—С.7. 2001. -
Лященко, Е.И. Лабораторные и практические работы по методике преподавания математики : учеб. пособие / Е. И. Лященко [и др.]; под ред. Е. И. Лященко. - Москва : Просвещение, 1988. - 223 с. : ил. - (Учебное пособие для педагогических институтов). - Библиогр.: с. 214-222. -
Мищенко Т.М. Дидактические материалы и методические рекомендации для учителя по геометрии: 8 класс: к учебнику Л.С. Атанасяна и др. «Геометрия. 7-9 классы». ФГОС (к новому учебнику) / Т.М. Мищенко. – М.: Издательство «Экзамен», 2016. – 174 с. -
Погорелов А.В. Геометрия. 7-9 классы : учеб. для общеобразоват. организаций/ А.В. Погорелов. – 2-е изд. – М. : Просвещение, 2014. – 240 с. -
Погорелов А.В. Геометрия: Учебник для 7-11 классов средней школы. М. 1987. -
Прицкер Б.С. Площадь четырехугольника // Математика в школе. – 1990. – №4. – С. 66-67. -
Саранцев, Г.И. Методика обучения математике: методология и теория [Текст]: учеб. пособие для студентов бакалавриата высших учебных заведений по направлению «Педагогическое образование» (профиль