ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 255
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 см.


 Решение: Подсчитав клетки, найдем: а = 6см, h = 3см. С помощью формулы получим: S = ∙
Решение: Подсчитав клетки, найдем: а = 6см, h = 3см. С помощью формулы получим: S = ∙






 a ∙ h =
a ∙ h =
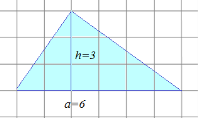
Рис.1. Треугольник
Фигура, представленная в виде многоугольника, дает возможность пользоваться следующими методами.
Метод разбиения:
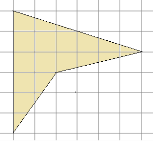 Для примера, методом разбиения нам необходимо вычислить площадь фигуры, которая изображена с размером клетки 1 см на 1 см на рисунке 2.
Для примера, методом разбиения нам необходимо вычислить площадь фигуры, которая изображена с размером клетки 1 см на 1 см на рисунке 2.
Решение. Существует большое количество способов разбиения. Для упрощения задачи мы можем разбить фигуру на прямоугольник и прямоугольные
треугольники, показанные на рисунке 3.






 Площади треугольников будут равны: S1
Площади треугольников будут равны: S1
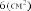
S2 = , S3 =












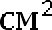

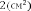
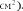 Сложив площади всевозможных фигур, получаем: S = 6 + 2 + 2 + 3 = 13(
Сложив площади всевозможных фигур, получаем: S = 6 + 2 + 2 + 3 = 13(
Рис.2. Многоугольник
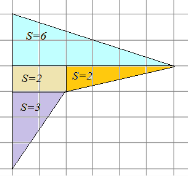
Рис.3. Метод
 разбиения
разбиения
Метод дополнительного построения:
В качестве примера, при помощи метода дополнительного построения нам потребуется вычислить площадь многоугольника, которая изображена с размером клетки 1см на 1 см на рисунке 2.
 Решение: Необходимо достроить данную фигуру до самого прямоугольника, на рисунке 4.
Решение: Необходимо достроить данную фигуру до самого прямоугольника, на рисунке 4.
Рис.4. Метод дополнения многоугольника
У большого прямоугольника площадь будет равна: Sб.пр. = 6 ∙ 6 = 36 см2.


 Внутренний прямоугольник: Sпр. = 3 ∙ 4 = 12см2. Площадь оставшихся треугольников: S1 = ∙6 ∙ 2 =
Внутренний прямоугольник: Sпр. = 3 ∙ 4 = 12см2. Площадь оставшихся треугольников: S1 = ∙6 ∙ 2 =




 6см2, S2 = =2см2,
6см2, S2 = =2см2,





 S3 = см2.
S3 = см2.
Рис.4. Метод
дополнения
Площадь искомой фигуры будет равна: S = 36 – 12 – 6 – 2 – 3 = 13см2. Также мы еще имеем право использовать метод, являющихся формулой Пика. Покажем ее на примере:
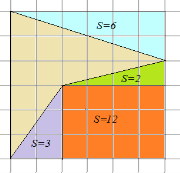
Нам дан многоугольник, имеющий только целочисленные вершины. Узлами решетки мы считаем точки, обе координаты которых целые. Многоугольник может являться и выпуклым и невыпуклым.




 Площадь многоугольника, данная с целочисленными вершинами будет равна: S = B + Г – целочисленное точки, находящиеся на границе
Площадь многоугольника, данная с целочисленными вершинами будет равна: S = B + Г – целочисленное точки, находящиеся на границе
многоугольника.
 К примеру, на изображенном рисунке 5 многоугольника.
К примеру, на изображенном рисунке 5 многоугольника.
В качестве примера нам дан рисунок 2, размер клетки 1см на 1 см. По формуле Пика нам нужно вычислить площадь
фигуры.
Рис.5. Узлы формулы Пика
Решение: Ориентируясь на рисунок 6, В = 9, Г =
Для вычисления площадей формула Пика является универсальной, она применима к любой фигуре. Но
есть большая вероятность допустить ошибку в подсчетах узлов решетки, если многоугольник
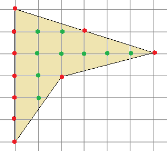
Рис.6. Многоугольник.
Формула Пика
занимает большую площадь. Исследуя подобные задачи ОГЭ, можно сделать вывод, что лучше пользоваться традиционными методами (дополнение или разбиение), а сам результат проверить с помощью формулы Пика.
Методическая система, включающая в себя планиметрические задачи по теме «Площадь многоугольника», ориентированная на формирование у школьников умений и навыков, применять теоретические знания к решению задач
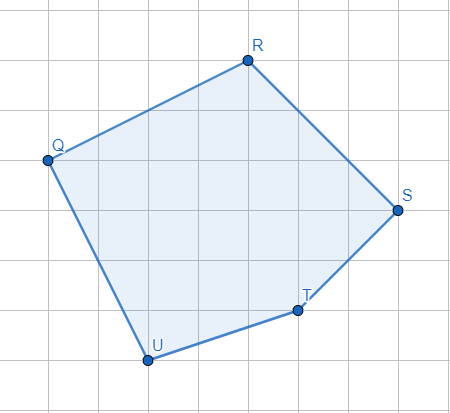
Рис.7. Многоугольник на клетчатой бумаге
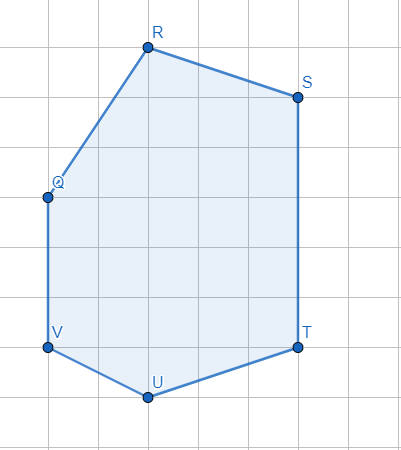
Рис.8. Многоугольник на
клетчатой бумаге
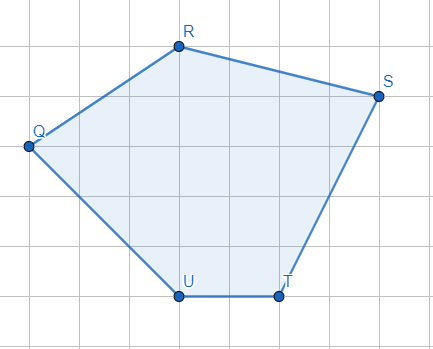
Рис.9. Многоугольник на клетчатой бумаге
Рис.10. Многоугольник на
33
параллелограмм QRST (Рис. 14). Найти
Задача №1. Найти площадь равностороннего треугольника со стороной равной стороне квадрата, площадь которого равна 16.
Дано: квадрат; Площадь квадрата равна 16;
Правильный треугольник; Сторона треугольника равна стороне квадрата.
Найти: Площадь треугольника.
 Решение. Так как площадь данного квадрата равна 16, то длина его стороны равна 4. Здесь учащимся необходимо напомнить, что площадь
Решение. Так как площадь данного квадрата равна 16, то длина его стороны равна 4. Здесь учащимся необходимо напомнить, что площадь


 правильного треугольника со стороной авычисляется по формуле .
правильного треугольника со стороной авычисляется по формуле .





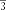 Согласно этой формуле получаем,
Согласно этой формуле получаем,


 Решение: Подсчитав клетки, найдем: а = 6см, h = 3см. С помощью формулы получим: S = ∙
Решение: Подсчитав клетки, найдем: а = 6см, h = 3см. С помощью формулы получим: S = ∙





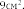 a ∙ h =
a ∙ h =
Рис.1. Треугольник
-
Фигура представлена многоугольником.
Фигура, представленная в виде многоугольника, дает возможность пользоваться следующими методами.
Метод разбиения:
-
Нахождение суммы всех площадей фигур;
-
Нахождение площади, получившихся фигур;
-
Разбиение многоугольника на треугольники и прямоугольники.
 Для примера, методом разбиения нам необходимо вычислить площадь фигуры, которая изображена с размером клетки 1 см на 1 см на рисунке 2.
Для примера, методом разбиения нам необходимо вычислить площадь фигуры, которая изображена с размером клетки 1 см на 1 см на рисунке 2.Решение. Существует большое количество способов разбиения. Для упрощения задачи мы можем разбить фигуру на прямоугольник и прямоугольные
треугольники, показанные на рисунке 3.






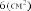
S2 = , S3 =













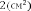
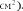 Сложив площади всевозможных фигур, получаем: S = 6 + 2 + 2 + 3 = 13(
Сложив площади всевозможных фигур, получаем: S = 6 + 2 + 2 + 3 = 13(Рис.2. Многоугольник

Рис.3. Метод
 разбиения
разбиенияМетод дополнительного построения:
-
До самого прямоугольника достроить фигуру;
-
Найти площадь прямоугольника и площадь, полученную дополнительными фигурами; -
От самой площади прямоугольника отнять площади всех оставшихся фигур.
В качестве примера, при помощи метода дополнительного построения нам потребуется вычислить площадь многоугольника, которая изображена с размером клетки 1см на 1 см на рисунке 2.
 Решение: Необходимо достроить данную фигуру до самого прямоугольника, на рисунке 4.
Решение: Необходимо достроить данную фигуру до самого прямоугольника, на рисунке 4.Рис.4. Метод дополнения многоугольника
У большого прямоугольника площадь будет равна: Sб.пр. = 6 ∙ 6 = 36 см2.


 Внутренний прямоугольник: Sпр. = 3 ∙ 4 = 12см2. Площадь оставшихся треугольников: S1 = ∙6 ∙ 2 =
Внутренний прямоугольник: Sпр. = 3 ∙ 4 = 12см2. Площадь оставшихся треугольников: S1 = ∙6 ∙ 2 =



 6см2, S2 = =2см2,
6см2, S2 = =2см2,




 S3 = см2.
S3 = см2.Рис.4. Метод
дополнения
Площадь искомой фигуры будет равна: S = 36 – 12 – 6 – 2 – 3 = 13см2. Также мы еще имеем право использовать метод, являющихся формулой Пика. Покажем ее на примере:
Нам дан многоугольник, имеющий только целочисленные вершины. Узлами решетки мы считаем точки, обе координаты которых целые. Многоугольник может являться и выпуклым и невыпуклым.




 Площадь многоугольника, данная с целочисленными вершинами будет равна: S = B + Г – целочисленное точки, находящиеся на границе
Площадь многоугольника, данная с целочисленными вершинами будет равна: S = B + Г – целочисленное точки, находящиеся на границемногоугольника.
 К примеру, на изображенном рисунке 5 многоугольника.
К примеру, на изображенном рисунке 5 многоугольника.В качестве примера нам дан рисунок 2, размер клетки 1см на 1 см. По формуле Пика нам нужно вычислить площадь
фигуры.
Рис.5. Узлы формулы Пика
Решение: Ориентируясь на рисунок 6, В = 9, Г =
-

 Используя формулу Пика: S = 9 + – 1 = 13см2.
Используя формулу Пика: S = 9 + – 1 = 13см2.
Для вычисления площадей формула Пика является универсальной, она применима к любой фигуре. Но
есть большая вероятность допустить ошибку в подсчетах узлов решетки, если многоугольник

Рис.6. Многоугольник.
Формула Пика
занимает большую площадь. Исследуя подобные задачи ОГЭ, можно сделать вывод, что лучше пользоваться традиционными методами (дополнение или разбиение), а сам результат проверить с помощью формулы Пика.
Методическая система, включающая в себя планиметрические задачи по теме «Площадь многоугольника», ориентированная на формирование у школьников умений и навыков, применять теоретические знания к решению задач
-
На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.7). Найти площадь данного многоугольника.
-
На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.1). Найти площадь данного многоугольника.
-
На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.9). Найти площадь данного многоугольника.
-
 На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.10). Найти площадь данного многоугольника.
На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.10). Найти площадь данного многоугольника.

Рис.7. Многоугольник на клетчатой бумаге

Рис.8. Многоугольник на
клетчатой бумаге

Рис.9. Многоугольник на клетчатой бумаге
Рис.10. Многоугольник на
-
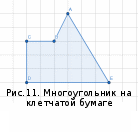 На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.11). Найти площадь данного многоугольника.
На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.11). Найти площадь данного многоугольника.
-
 На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.12). Найти площадь данного многоугольника.
На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.12). Найти площадь данного многоугольника.
-
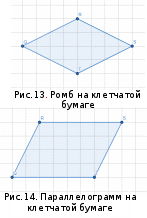 На клетчатой бумаге с размерами клетки 4×4 задан ромб QRST (Рис.13). Найти
На клетчатой бумаге с размерами клетки 4×4 задан ромб QRST (Рис.13). Найти-
площадь ромба; -
длины диагоналей ромба; -
тангенс его острого угла; -
тангенс его тупого угла; -
радиус окружности, вписанной в ромб.
-
-
На клетчатой бумаге с размерами клетки 4×4 задан
33
параллелограмм QRST (Рис. 14). Найти
-
площадь параллелограмма; -
длину диагонали QS; -
длину диагонали RT; -
тангенс ∠RST; -
синус ∠RQT; -
косинус ∠QTS; -
синус угла между его диагоналями.
-
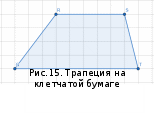 На клетчатой бумаге с размерами клетки 4×4 задана трапеция QRST (Рис. 15). Найти
На клетчатой бумаге с размерами клетки 4×4 задана трапеция QRST (Рис. 15). Найти
-
площадь трапеции; -
среднюю линию трапеции; -
длины боковых сторон трапеции; -
косинусы тупых углов трапеции; -
косинусы острых углов трапеции.
Задача №1. Найти площадь равностороннего треугольника со стороной равной стороне квадрата, площадь которого равна 16.
Дано: квадрат; Площадь квадрата равна 16;
Правильный треугольник; Сторона треугольника равна стороне квадрата.
Найти: Площадь треугольника.
 Решение. Так как площадь данного квадрата равна 16, то длина его стороны равна 4. Здесь учащимся необходимо напомнить, что площадь
Решение. Так как площадь данного квадрата равна 16, то длина его стороны равна 4. Здесь учащимся необходимо напомнить, что площадь

 правильного треугольника со стороной авычисляется по формуле .
правильного треугольника со стороной авычисляется по формуле .




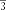 Согласно этой формуле получаем,
Согласно этой формуле получаем,