ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 238
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
что .

 Ответ: .
Ответ: .

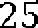
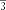 Задача №2. Найти площадь квадрата со стороной равной стороне правильного треугольника площади .
Задача №2. Найти площадь квадрата со стороной равной стороне правильного треугольника площади .
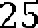
 Дано: правильный треугольник; Площадь треугольника равна ;
Дано: правильный треугольник; Площадь треугольника равна ;
Сторона квадрата равна стороне треугольника.
Найти: Площадь квадрата.

 Решение. Учащимся необходимо обратить внимание на тот факт, что эта задача взаимосвязана с предыдущей. Поскольку в ней известна площадь правильного треугольника, а найти следует площадь квадрата. Используем известную формулу для вычисления площади правильного треугольника
Решение. Учащимся необходимо обратить внимание на тот факт, что эта задача взаимосвязана с предыдущей. Поскольку в ней известна площадь правильного треугольника, а найти следует площадь квадрата. Используем известную формулу для вычисления площади правильного треугольника








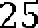
 . Составляем уравнение . Откуда находим, что
. Составляем уравнение . Откуда находим, что 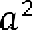
Поскольку площадь квадрата равна квадрату длины его стороны, значит, она равна 100.
Ответ: 100.
Задача №3. Найти площадь квадрата со стороной равной диагонали прямоугольника со сторонами 3 см. и 4 см.
Дано: прямоугольник;
Стороны прямоугольника равны 3см. и 4 см.
Квадрат; Сторона квадрата равна стороне треугольника. Найти: Площадь квадрата.
Решение: Обозначим заданный прямоугольник через ABCD. Пусть АВ=3см, а CD=4см. Важно обратить внимание учащихся на тот факт, что





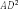 треугольник ADC является прямоугольным. Значит, к нему можно применить теорему Пифагора. Следовательно,
треугольник ADC является прямоугольным. Значит, к нему можно применить теорему Пифагора. Следовательно, 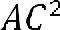
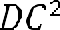
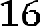

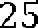 . Так как сторона квадрата равна диагонали, то площадь этого
. Так как сторона квадрата равна диагонали, то площадь этого
квадрата будет равна квадрату диагонали. Таким образом, получаем, что площадь квадрата равна 25.
Ответ: 25.
Задача №4. Найти сторону квадрата, зная, что он равновелик с параллелограммом,
боковая сторона которого равна 5см, а высота, проведенная к этой стороне равна 6 см.
Дано: параллелограмм АBCD; АВ=5см, DH= 6 см. ;
Квадрат; Площадь квадрата равна площади параллелограмма; Найти: сторону квадрата.


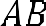
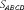 Решение. В начале решения этой задачи необходимо вспомнить совместно с учениками формулу для вычисления площади параллелограмма. Важно отметить, что эта формула справедлива как в случае, когда основанием служит сторона AD, так и в случае, когда основанием служит боковая сторона АВ. Согласно этой формуле получаем, что
Решение. В начале решения этой задачи необходимо вспомнить совместно с учениками формулу для вычисления площади параллелограмма. Важно отметить, что эта формула справедлива как в случае, когда основанием служит сторона AD, так и в случае, когда основанием служит боковая сторона АВ. Согласно этой формуле получаем, что



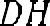
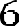
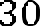
 . Так как площадь квадрата с одной стороны равна площади параллелограмма, а с другой стороны квадрату его стороны, значит, сторона квадрата равна .
. Так как площадь квадрата с одной стороны равна площади параллелограмма, а с другой стороны квадрату его стороны, значит, сторона квадрата равна .
 Ответ: .
Ответ: .
Задача №5. Найти сторону квадрата, зная, что он равновелик с трапецией, диагонали которой равны 15 см и 12 см, а угол между ними равен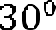 .
.
Дано: трапеция АBCD;
 АС=15см, ВD= 12 см. ,
АС=15см, ВD= 12 см. , 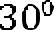 ;
;
Квадрат ; Площадь квадрата равна площади трапеции ABCD; Найти: сторону квадрата.
Решение. Важно обратить внимание учащихся на тот факт, что для вычисления площади трапеции можно использовать различные формулы и способы. В данном случае трапеция задана диагоналями и углом между ними, поэтому для нее можно использовать более общую формулу, которую обычно используют для вычисления площади четырехугольника. Здесь важное значение приобретает тот факт, что трапеция это есть частный случай четырехугольника. Таким образом, получаем, что





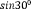




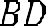
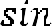
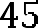
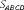
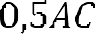
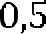 .
.

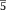
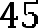 Поскольку заданный нам квадрат имеет площадь равную площади трапеции, то квадрат его стороны х равен 45. Значит имеем уравнение . Решая это уравнение, находим, что сторона квадрата равна .
Поскольку заданный нам квадрат имеет площадь равную площади трапеции, то квадрат его стороны х равен 45. Значит имеем уравнение . Решая это уравнение, находим, что сторона квадрата равна .
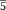 Ответ:
Ответ:
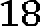
 Задача №6. Найти сторону правильного треугольника, зная, что его площадь численно равна площади параллелограмма ABCD с диагоналями AC= см и BD=22 см и углом между ними
Задача №6. Найти сторону правильного треугольника, зная, что его площадь численно равна площади параллелограмма ABCD с диагоналями AC= см и BD=22 см и углом между ними 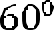 .
.
Дано: параллелограмм АBCD;
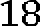
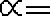
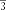 АС= см, ВD= 22 см. ,
АС= см, ВD= 22 см. , 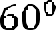 ;
;
Правильный треугольник ;
Площадь правильного треугольника равна площади параллелограмма ABCD; Найти: сторону треугольника.
 Решение. Обычно учащиеся правильно решившие предыдущую задачу и хорошо усвоившие ход ее решения быстро ориентируются в том, что параллелограмм это тоже частный случай четырехугольника. Поэтому для вычисления его площади можно использовать более общую формулу, а именно ту, которую мы использовали при решении предыдущей
Решение. Обычно учащиеся правильно решившие предыдущую задачу и хорошо усвоившие ход ее решения быстро ориентируются в том, что параллелограмм это тоже частный случай четырехугольника. Поэтому для вычисления его площади можно использовать более общую формулу, а именно ту, которую мы использовали при решении предыдущей

 Ответ: .
Ответ: .
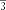 Задача №2. Найти площадь квадрата со стороной равной стороне правильного треугольника площади .
Задача №2. Найти площадь квадрата со стороной равной стороне правильного треугольника площади . Дано: правильный треугольник; Площадь треугольника равна ;
Дано: правильный треугольник; Площадь треугольника равна ;Сторона квадрата равна стороне треугольника.
Найти: Площадь квадрата.

 Решение. Учащимся необходимо обратить внимание на тот факт, что эта задача взаимосвязана с предыдущей. Поскольку в ней известна площадь правильного треугольника, а найти следует площадь квадрата. Используем известную формулу для вычисления площади правильного треугольника
Решение. Учащимся необходимо обратить внимание на тот факт, что эта задача взаимосвязана с предыдущей. Поскольку в ней известна площадь правильного треугольника, а найти следует площадь квадрата. Используем известную формулу для вычисления площади правильного треугольника







 . Составляем уравнение . Откуда находим, что
. Составляем уравнение . Откуда находим, что Поскольку площадь квадрата равна квадрату длины его стороны, значит, она равна 100.
Ответ: 100.
Задача №3. Найти площадь квадрата со стороной равной диагонали прямоугольника со сторонами 3 см. и 4 см.
Дано: прямоугольник;
Стороны прямоугольника равны 3см. и 4 см.
Квадрат; Сторона квадрата равна стороне треугольника. Найти: Площадь квадрата.
Решение: Обозначим заданный прямоугольник через ABCD. Пусть АВ=3см, а CD=4см. Важно обратить внимание учащихся на тот факт, что




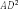 треугольник ADC является прямоугольным. Значит, к нему можно применить теорему Пифагора. Следовательно,
треугольник ADC является прямоугольным. Значит, к нему можно применить теорему Пифагора. Следовательно, 
квадрата будет равна квадрату диагонали. Таким образом, получаем, что площадь квадрата равна 25.
Ответ: 25.
Задача №4. Найти сторону квадрата, зная, что он равновелик с параллелограммом,
боковая сторона которого равна 5см, а высота, проведенная к этой стороне равна 6 см.
Дано: параллелограмм АBCD; АВ=5см, DH= 6 см. ;
Квадрат; Площадь квадрата равна площади параллелограмма; Найти: сторону квадрата.


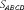 Решение. В начале решения этой задачи необходимо вспомнить совместно с учениками формулу для вычисления площади параллелограмма. Важно отметить, что эта формула справедлива как в случае, когда основанием служит сторона AD, так и в случае, когда основанием служит боковая сторона АВ. Согласно этой формуле получаем, что
Решение. В начале решения этой задачи необходимо вспомнить совместно с учениками формулу для вычисления площади параллелограмма. Важно отметить, что эта формула справедлива как в случае, когда основанием служит сторона AD, так и в случае, когда основанием служит боковая сторона АВ. Согласно этой формуле получаем, что


 . Так как площадь квадрата с одной стороны равна площади параллелограмма, а с другой стороны квадрату его стороны, значит, сторона квадрата равна .
. Так как площадь квадрата с одной стороны равна площади параллелограмма, а с другой стороны квадрату его стороны, значит, сторона квадрата равна . Ответ: .
Ответ: .Задача №5. Найти сторону квадрата, зная, что он равновелик с трапецией, диагонали которой равны 15 см и 12 см, а угол между ними равен
Дано: трапеция АBCD;
 АС=15см, ВD= 12 см. ,
АС=15см, ВD= 12 см. , Квадрат ; Площадь квадрата равна площади трапеции ABCD; Найти: сторону квадрата.
Решение. Важно обратить внимание учащихся на тот факт, что для вычисления площади трапеции можно использовать различные формулы и способы. В данном случае трапеция задана диагоналями и углом между ними, поэтому для нее можно использовать более общую формулу, которую обычно используют для вычисления площади четырехугольника. Здесь важное значение приобретает тот факт, что трапеция это есть частный случай четырехугольника. Таким образом, получаем, что





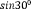




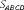

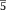
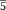 Ответ:
Ответ: Задача №6. Найти сторону правильного треугольника, зная, что его площадь численно равна площади параллелограмма ABCD с диагоналями AC= см и BD=22 см и углом между ними
Задача №6. Найти сторону правильного треугольника, зная, что его площадь численно равна площади параллелограмма ABCD с диагоналями AC= см и BD=22 см и углом между ними Дано: параллелограмм АBCD;
 АС= см, ВD= 22 см. ,
АС= см, ВD= 22 см. , Правильный треугольник ;
Площадь правильного треугольника равна площади параллелограмма ABCD; Найти: сторону треугольника.
 Решение. Обычно учащиеся правильно решившие предыдущую задачу и хорошо усвоившие ход ее решения быстро ориентируются в том, что параллелограмм это тоже частный случай четырехугольника. Поэтому для вычисления его площади можно использовать более общую формулу, а именно ту, которую мы использовали при решении предыдущей
Решение. Обычно учащиеся правильно решившие предыдущую задачу и хорошо усвоившие ход ее решения быстро ориентируются в том, что параллелограмм это тоже частный случай четырехугольника. Поэтому для вычисления его площади можно использовать более общую формулу, а именно ту, которую мы использовали при решении предыдущей