Файл: 3.doc

По ДЕСТу 8239-72 (додаток 6) приймаємо двутавр №22а, у якого: I_y=206см⁴; =32.8см²; b=12см.

Момент інерції:

Радіус інерції:

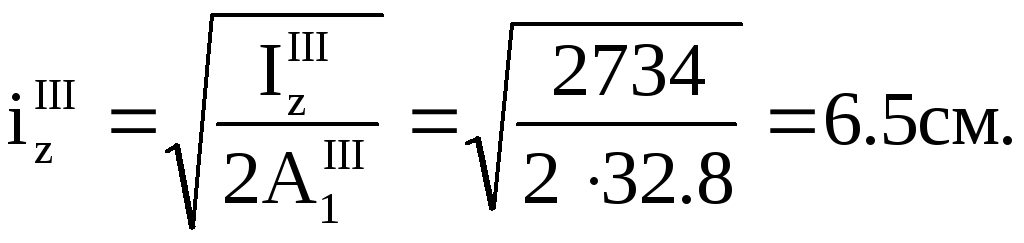
Гнучкість стійки:

.

Ці гнучкості відповідає (додаток 5):

.

ІV наближення ,

.

.

Ми бачимо, що по ДЕСТу 8239-72 (додаток 6) необхідно знову брати двутавр №22а, так як двутавр №22 має А₁=30.6см², що менше А₄=30.85см².

Перевіримо яке еквівалентне напруження буде виникати в стійці із двутавра №22а:

160МПа.

Недонапруження складе:

5.

Спробуємо взяти двутавр №22, у якого ;I_y=157см⁴; b=11см; і_y=9.13см.

Радіус інерції:

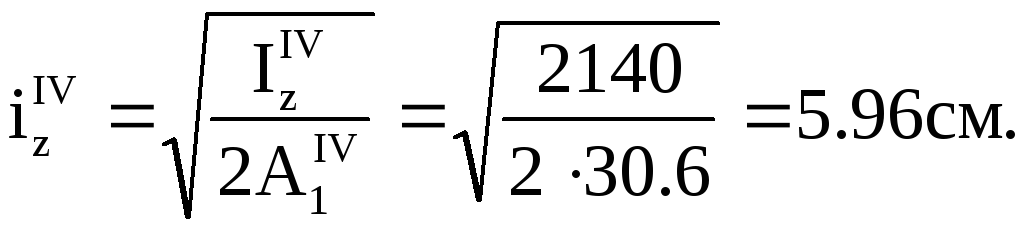
Гнучкість:

Що відповідає:

.

Еквівалентне напруження буде:

,

_е=164МПа_ст=160МПа.

Перенапруження складає:

5.

Тому можна підбір перерізу на цьому закінчити.

Перевіримо стійкість стержня в плоскості XOZ для двутавра №22.

Гнучкість:

,

.

А тому стійкість стійки, яка складається з двох двутаврів №22 в обох площинах забезпечена.

12. Наближений розрахунок на удар

Напруження і переміщення, викликані дією ударного навантаження, в k_д раз більше напружень і переміщень, які викликані дією такого ж по величині, але статично прикладеного навантаження, тобто

_д=k_д_ст;

_д=k_д_ст;

_д=k_д_ст.

Динамічний коефіцієнт розраховують по наступній формулі, яка отримана без врахування власної ваги системи, яка піддається удару:

,

де h – висота падіння вантажу,

_ст – величина переміщення від статичної дії сили, яка дорівнює вазі вантажу, який вдаряє.

Якщо врахувати, що (v – швидкість вантажу, який падає, на початку удару), то отримаємо

.

Приклад 1

На стальний ломаний брус, зображений на рис.12.1,а, падає вантаж Q.

Визначити максимальні розрахункові напруження в конструкції (без врахування її маси), а також вертикальне переміщення перерізу А.

Елемент АВ вважати абсолютно жорстким.

Брус ВКС зазнає згину силою Q і кручення моментом Qa – схема навантаження приведена на рис.12.1,б.

Для визначення небезпечного перерізу бруса ВКС побудуємо епюри згинаючих моментів М_z і крутних моментів М_x. Епюра М_z, згідно схемі навантаження рис.12.2,a, представлена на рис.12.2,б, а епюра М_x та схема навантаження, дані на рис.12.2,д,е. Із аналізу цих епюр робимо висновок, що небезпечним може бути або переріз С, або К. Хоча для другого М_z менше, чим для першого, але і діаметр його теж менше. Той переріз, для якого статичні еквівалентні напруження виявляться більшими, є небезпечним.

Переріз С:

М_z=Q(l₁+l₂)=250(60+120)=45000Нсм;

М_x=Qа=25050=12500Нсм.

а)б)

Рис.12.1

Статичні еквівалентні напруження розрахуємо по гіпотезі найбільших дотичних напружень:

де .

Переріз К: М_z=Ql₂=250120=30000Нсм; М_x=Qа=12500Нсм;

де .

Отже, небезпечним є переріз К.

Визначимо статичне вертикальне переміщення перерізу А. Повне переміщення можна розглядати як суму переміщення f₁, обумовленого згином бруса ВКС і переміщення f₂, обумовленого закручуванням того ж бруса (рис.12.1,б).

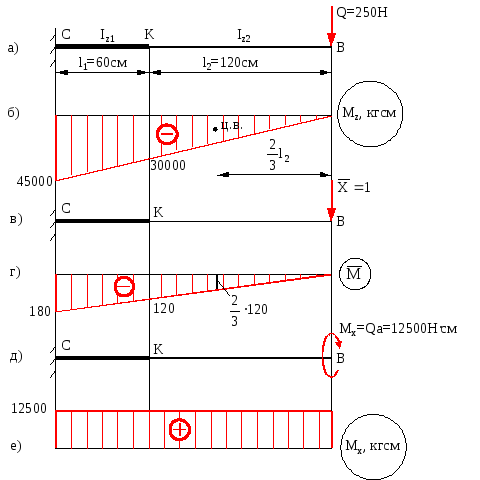
Рис.12.2

Переміщення f₁ дорівнює прогину f_В перерізу В від сили Q (нагадаємо, що по умові задачі брус АВ - абсолютно жорсткий):

f₂=_Ba,

де _B – кут повороту перерізу В бруса ВКС в результаті його закручування.

Величину f₁ визначимо методом Мора з застосуванням правила Верещагіна (рис.12.2,а-г):

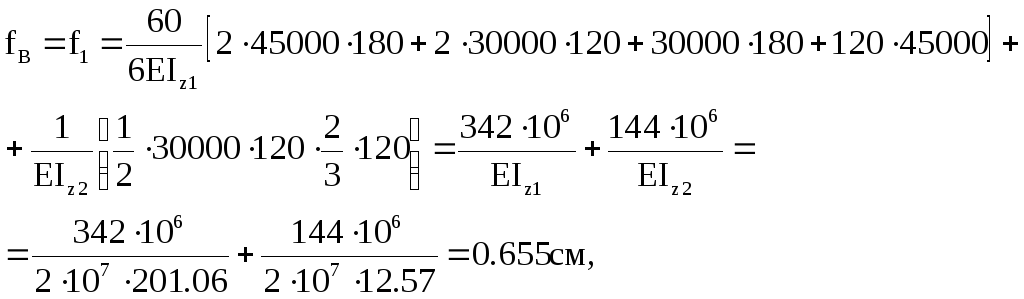
де ;.

Знаходимо кут повороту перерізу В:

де ;.

Переміщення, обумовлене закручуванням бруса

f₂=a_B=507.6910^-3=0.3845см.

Статичне вертикальне переміщення перерізу А

_ст=f_A=f₁+f₂=0.655+0.3845=1.04см.

Визначаємо динамічний коефіцієнт:

.

Для небезпечного перерізу К максимальні еквівалентні динамічні напруження

.

Динамічне вертикальне переміщення перерізу А

_д=k_д_ст=3.61.04=3.74см.

Приклад 2

На стальний ступінчастий стержень падає вантаж Q (рис.12.3). Вважаючи, що стійкість стержня забезпечена, визначити найбільше стискаюче напруження, яке виникає в поперечному перерізі стержня.

Максимальні статичні (стискаючі) напруження

де .

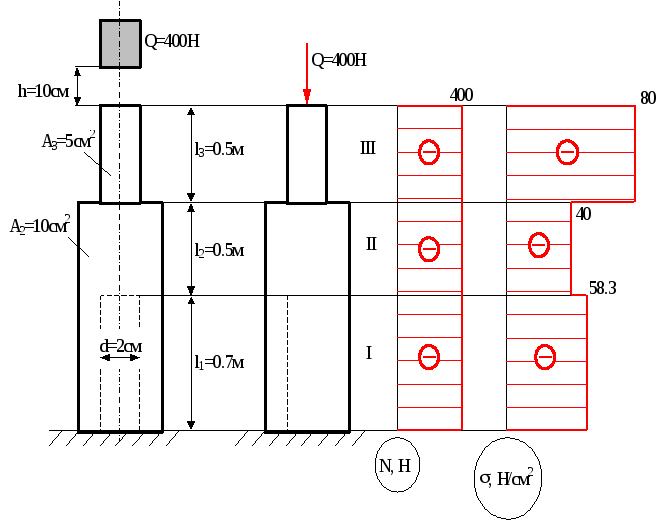
Рис.12.3

Статичне переміщення в місці удару дорівнює, очевидно, вкороченню стержня при статичному прикладенні вантажу Q:

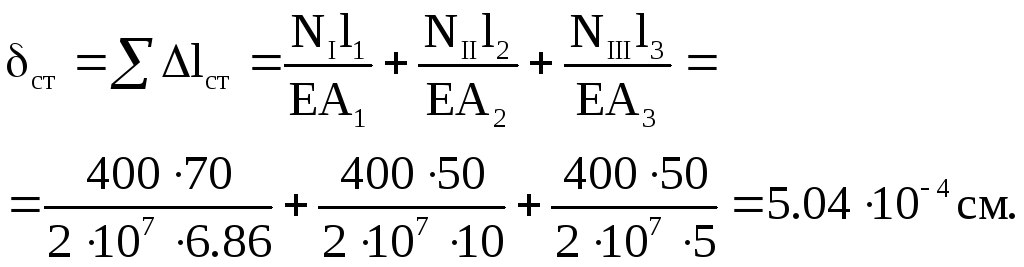
Визначаємо динамічний коефіцієнт:

.

Динамічне напруження

_д=k_д_ст=200.2180=16016.6Н/см².

Динамічне переміщення

_д=k_д_ст=200.215.0410^-4=0.1см.

Отриманий результат має сенс лише при умові, що межа пропорційності матеріалу стержня вище знайденого динамічного напруження.