Файл: 3.doc

В системі координат z0 і y0, знаходимо центр ваги складного перерізу с і проводимо головні центральні осі zc і yc (ось yc для даного перерізу є головною як ось симетрії).

Визначимо головний центральний момент інерції відносно осі Y_C (додаток 7):

Застосовуючи формули моментів інерції при паралельному переносі осей визначимо головний центральний момент інерції відносно осі Z_C:

де а₁=y₁-y_C=12.55-7.76=4.79см, а₂=y₂-y_C=5-7.76=-2.76см,

а₃=y₃-y_C=1-7.76=-6.76см – відстані від центру ваги півкола, прямокутника і трикутника до центральної осі Z_C.

Координати точки прикладення рівнодіючої F в центральні системі координат Z_С і Y_С.

y_F=8см; z_F=-5см.

Площа перерізу:

А=А₁+A₂-А₃=56.55+120-9=167.55см².

Радіуси інерції:

, .

Визначимо положення нейтральної лінії відносно поперечного перерізу бруса.

З рівняння нейтральної осі:

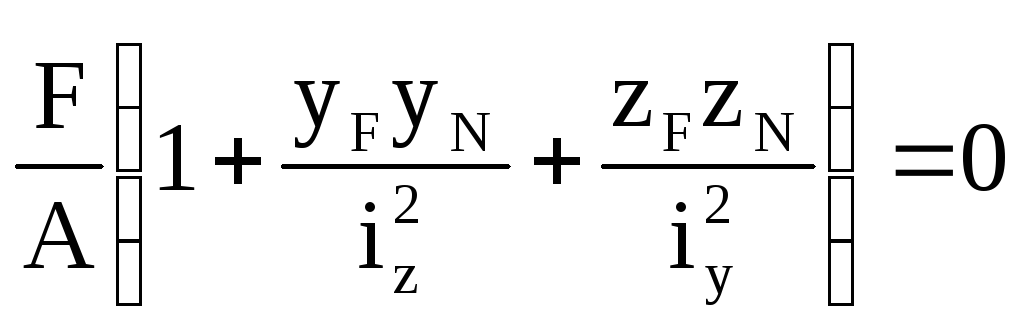
при z_N=0 знайдемо, що:

Аналогічно, при y_N=0

Проводимо нейтральну лінію. Так як нейтральна лінія проходить через перерізи стержня, то в поперечному перерізі його одночасно діють стискаючі і розтягуючі напруження.

Тому, для матеріалу стержня, неоднаково працюючому на стиск і розтяг, необхідна перевірка по умовам міцності на стиск і розтяг.

З рівнянь міцності визначаємо допустиме навантаження:

,

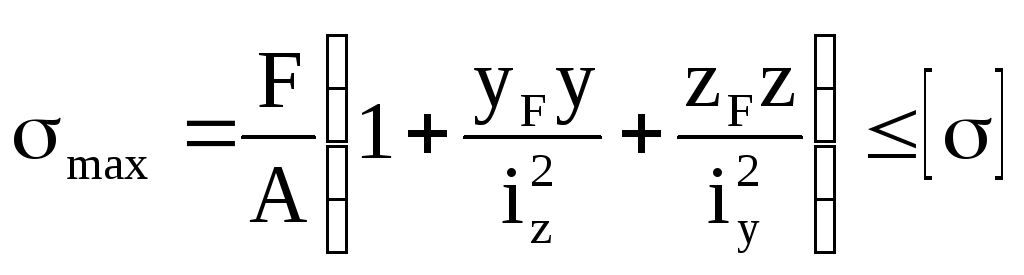звідки:

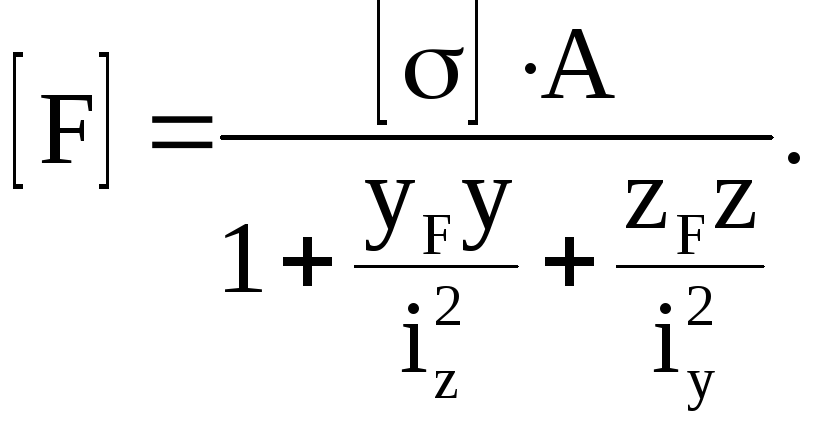
Величина навантаження [F] в зоні стиску, з рівняння міцності для найбільш віддаленої від нейтральної осі точки А.

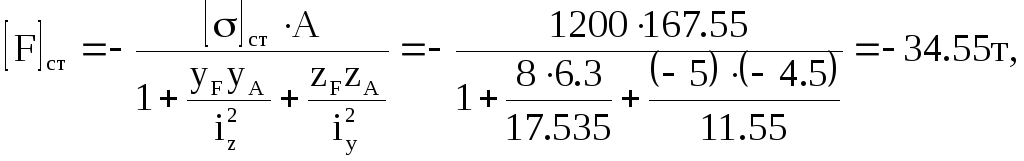
де y_A=6.3см і z_A=-4.5см – координати небезпечної точки (т.А) в центральній системі осей в зоні стиску.

Величина навантаження [F] в зоні розтягу:

де y_B=-7.76см і z_B=6см – координати небезпечної точки (т.B)

Знак “-” тому, що сила F стискуюча.

З двох отриманих значень за допустиме навантаження приймаємо найменше по модулю:

[F]=9.78т

Знаючи величину навантаження F, визначаємо напруження в характерних точках перерізу, підставивши в формулу для напружень 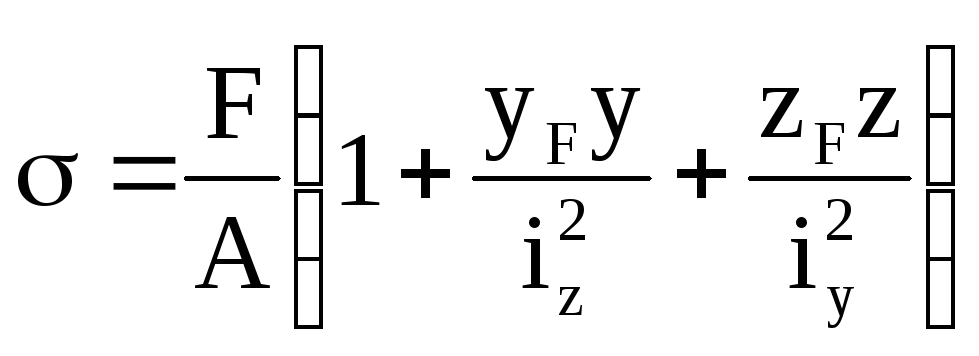координати цих точок в головній центральній системі осей:

Точка 1 (y₁=8.24см; z₁=0)

Точка А (y_А=6.3см; z_А=-4.5см)

Точка 2 (y₂=2.3см; z₂=-6см)

Точка 3 (y₃=-7.76см; z₃=-6см)

Точка 4 (y₄=-7.76см; z₄=-3см)

Точка 5 (y₅=-4.76см; z₅=0)

Рис.7.3

Точка 6 (y₆=-7.76см; z₆=3см)

Точка В (y_В=-7.76см; z_В=6см)

Точка 7 (y₇=2.3см; z₇=6см)

Знайдені напруження в точках в масштабі відкладаємо на аксонометричному рисунку стержня. Отримаємо просторову епюру розподілу напружень в перерізі стержня (рис.7.3).

Наприклад, побудуємо епюру розподілу напружень на лінії 3-4.

Для цього відкладаємо напруження в точці 4 і, так як воно додатне, спрямовуємо його вверх. З кінця вектора ₄ проводимо пряму лінію через нульову точку К (так як тут н.о. перетинає цю грань) до перетину з ребром 3 стержня. Отриманий відрізок на ребрі в масштабі дасть напруження в точці 3. І так далі.

8. Згин з крученням

Згин з крученням зустрічається найбільш часто при розрахунку валів круглого поперечного перерізу.

Розрахунок валу полягає, як правило, у визначенні необхідного діаметру (або діаметрів – якщо вал пустотілий) при заданому навантаженні, яке сприймається валом.

При одночасній дії згину і кручення в поперечному перерізі валу діють як дотичні, так і нормальні напруження, і матеріал знаходиться в плоскому напруженому стані. Для визначення розрахункового напруження в небезпечній точці використовують одну із теорій міцності. Частіше всього використовують ІІІ теорію найбільших дотичних напружень або IV – енергетичну теорію формозміни.

При крученні максимальні дотичні напруження виникають в кожній точці контуру перерізу. Тому при спільні дії кручення і згину небезпечними будуть дві точки перерізу вала, де одночасно з найбільшими дотичними напруженнями діють найбільші нормальні напруження (в одні точці – розтягуюче, а в другій – стискаюче).

З метою зменшення об’єму обчислень розрахункові напруження, визначають по формулам:

,

і в даному випадку виражають через внутрішні сили і геометричну характеристику перерізу, враховуючи умови міцності по ІІІ і IV теоріях:

або

де М – величина згинаючого моменту в небезпечному перерізі,

М_кр – величина крутного моменту в небезпечному перерізі,

W_z – осьовий момент опору перерізу.

Так як у випадку круглого перерізу косий згин бруса неможливий, то для визначення небезпечного перерізу і значення М в цьому перерізі доцільно побудувати спочатку епюри згинаючих моментів M_z і M_y в горизонтальній і вертикальній площинах. Тоді ординати сумарної епюри згинаючих моментів визначаються як геометрична сума моментів M_z і M_y у відповідних перерізах.

Вектори М в різних перерізах знаходяться в різних площинах (які проходять через ось валу). Тому для зручності при побудові сумарної епюри їх умовно поєднують в площині креслення і знак згинаючого моменту не вказують.

Належить відмітити, що на ділянках, де прямі, які обмежують епюри M_z і M_y, перетинаються з віссю епюр в різних точках, епюра М обмежується кривою, орієнтованою опуклістю вниз (до осі).

Приклад

Стальний вал трансмісії робить n об/хв і передає через два ведених шківа потужності N₂ і N₃, діаметри шківів D₁=0.8м, D₂=0.6м, D₃=0.5м, а=1м. Визначити діаметр вала, якщо []=100МН/м², N₂=50кВт, N₃=30кВт, ₁=60⁰, ₂=120⁰, n=955об/хв.

Визначаємо потужність на ведучому шківі:

N₁=N₂+N₃=50+30=80кВт.

Визначаємо крутні моменти, які виникають на кожному шківі:

,

,

.

Крутні моменти на окремих ділянках вала будуть:

На ділянці cd

М_кр=0.3кНм.

На ділянці de

М_кр=0.8кНм.

По отриманим даним будуємо епюру крутних моментів (рис.8.2,б).

Розрахуємо тиск, який передається шківами на вал, вважаючи натяг ведучої гілки паса в два рази більшим, чим натяг веденої.

Розглянувши рис.8.1,б можна записати:

,

але Т_і=2t_i

,

звідки: ,

де t_i – натяг веденої гілки паса і-того шківа,

T_i - натяг ведучої гілки паса і-того шківа.

Тиск на вал запишеться так:

F_і=Т_і+t_і=2t_і+t_і

звідки: F_і=3t_і.

а)б)

Рис.8.1

Натяг веденої гілки паса кожного шківа буде: