ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 289
Скачиваний: 0
СОДЕРЖАНИЕ
5. Геометричні характеристики поперечних перерізів бруса.
Зміна моментів інерції при повороті осей. Головні осі і головні моменти інерції
6. Розрахунок на міцність при згині
7. Позацентровий розтяг (стиск) стержня високої жорсткості
9. Визначення переміщень в пружних системах
10. Статично невизначені системи
11. Розрахунок стиснутих стержнів на стійкість
12. Наближений розрахунок на удар
Механічні характеристики вуглецевих конструкційних сталей
Додаток 2 Механічні характеристики чавуну
Додаток 3 Орієнтовні значення основних допустимих напруг на розтяг і стиск
Ділянка
АВ:
![]()
MF1=0,
![]()
Ділянка
ВC:
![]()
![]()
![]()
Ділянка CD: 0x3l
![]()
![]()
Кут повороту перерізу В

Розрахований кут повороту має додатній знак, отже напрямок повороту перерізу співпадає з напрямком одиничного моменту.
2. Спосіб Верещагіна.
Будуємо
епюру згинаючих моментів МF
від заданого навантаження (вантажну).
Вона представлена на рис.9.4,б. В тому
перерізі, де необхідно визначити прогин,
прикладаємо одиничну силу
![]() (рис.9.4,в) і будуємо від неї одиничну
епюру згинаючих моментів
(рис.9.4,в) і будуємо від неї одиничну
епюру згинаючих моментів![]() (рис.9.4,г). Виконуючи перемноження
вантажної епюри МF
і одиничної епюри
(рис.9.4,г). Виконуючи перемноження
вантажної епюри МF
і одиничної епюри
![]() отримаємо лінійне переміщення перерізу
А:
отримаємо лінійне переміщення перерізу
А:
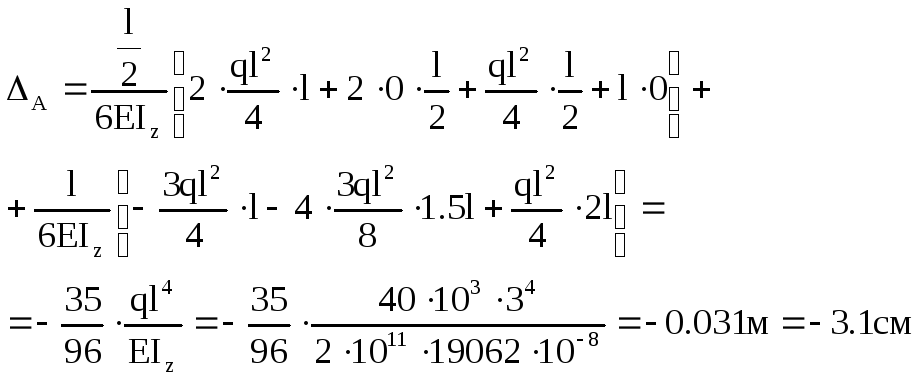
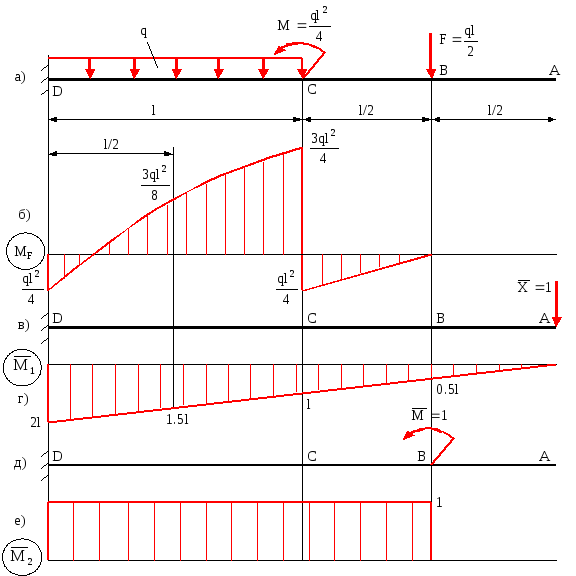
Рис.9.4
В
тому перерізі де необхідно визначити
кут повороту прикладаємо одиничний
момент
![]() (рис.9.4,д) і будуємо від нього одиничну
епюру згинаючих моментів
(рис.9.4,д) і будуємо від нього одиничну
епюру згинаючих моментів![]() (рис.9.4,е). Виконуючи перемноження
вантажної епюри МF
і одиничної епюри
(рис.9.4,е). Виконуючи перемноження
вантажної епюри МF
і одиничної епюри
![]() отримаємо кут повороту перерізу В:
отримаємо кут повороту перерізу В:

10. Статично невизначені системи
Статично невизначеними називаються системи, силові фактори в елементах яких не можуть бути визначені тільки з рівнянь рівноваги твердого тіла. В таких системах зв’язків більше, чим це необхідно для рівноваги. Таким чином, частина зв’язків є зайвою, а відповідні зусилля є зайвими невідомими. По числу зайвих зв’язків або зайвих невідомих зусиль встановлюють ступінь статичної невизначеності системи.
Ступінь статичної невизначеності плоских систем може бути визначена по формулі
s=3k-ш
де k – число замкнутих контурів,
ш – число шарнірів в перерахунку на поодинокі.
Основа (земля) розглядається як стержень нескінченної жорсткості (ЕІ=).
При розрахунку статично невизначених систем можна в якості невідомих приймати як сили або силові фактори, так і переміщення або деформаційні фактори. В першому випадку маємо так званий метод сил, в другому – метод переміщень.
Розрахунок по методу сил проводять в такій послідовності.
Встановлюють ступінь статичної невизначеності.
Шляхом видалення зайвих зв’язків замінюють початкову систему статично визначеною, яка називається основною системою. Таких систем можна побудувати кілька, тому необхідно додержуватись при цьому умови їх геометричної незмінності.
Основну систему навантажують заданими зовнішніми силами і зайвими невідомими зусиллями, які заміняють дію видалених зв’язків, в результаті чого отримують еквівалентну систему.
Для забезпечення еквівалентності початкової і основної систем невідомі зусилля повинні бути підібрані так, щоб деформації основної системи не відрізнялись від деформацій початкової статично невизначеної системи. Для цього переміщення точок прикладення зайвих невідомих по напрямку їх дії прирівнюють до нуля. З отриманих таким чином рівнянь визначають значення зайвих невідомих зусиль. Визначення переміщень відповідних точок можна виконувати будь яким способом, однак краще використовувати при цьому найбільш загальний метод Мора.
Додаткові рівняння переміщень, які виражають рівність нулю переміщень по напрямку зайвих невідомих, зручно складати в так звані канонічній формі, тобто по визначеній закономірності.
Рівняння переміщень для будь-якої n раз статично невизначеної системи в канонічній формі можуть бути записані так
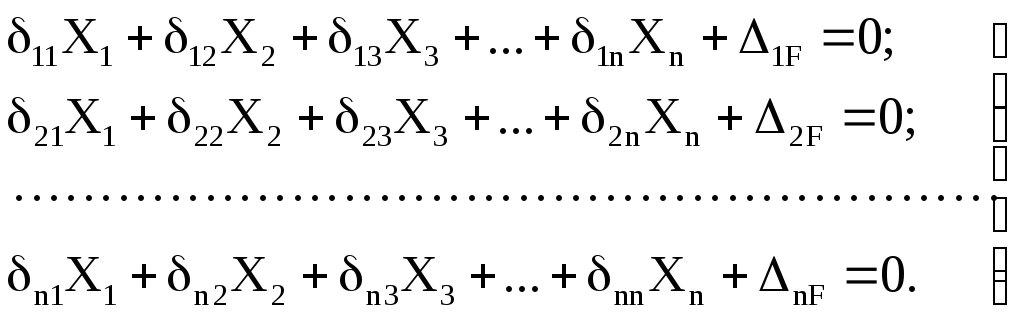
Приклад
Для заданої статично невизначеної рами (рис.10.1) побудувати епюри поперечних сил, осьових зусиль і згинаючих моментів, а також підібрати двутавровий переріз.
Допустиме напруження матеріалу рами []=160МН/м2, а=1м, q=2кН/м, F=5кН, М=3кНм.
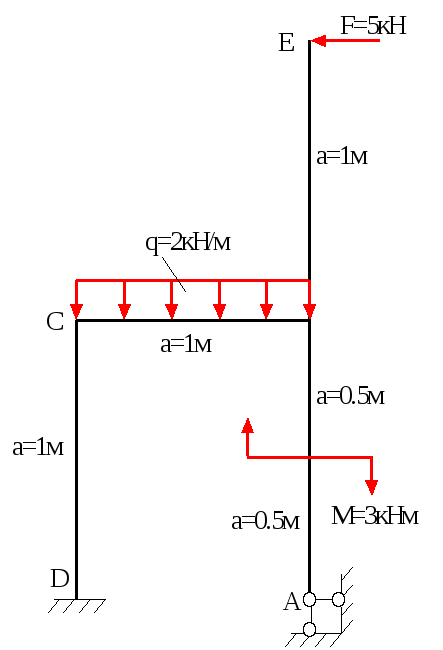
Рис.10.1
Дана задача двічі статично невизначена, так як
S=3к-Ш=32-4=2,
де S – ступінь статичної невизначеності рами,
к=2 – число замкнутих контурів,
Ш=4 – число поодиноких шарнірів.
Із статично невизначеної системи шляхом видалення зв’язків отримуємо основну систему (тобто статично визначену і геометрично незмінну систему) (рис.10.2,а).
Відкидаючи опору А і замінивши її дію на раму невідомими реакціями X1 і X2, які прикладаємо в довільному напрямку, а також прикладаючи до основної системи зовнішні навантаження, отримуємо еквівалентну систему (рис.10.2,б).
а) б)
б)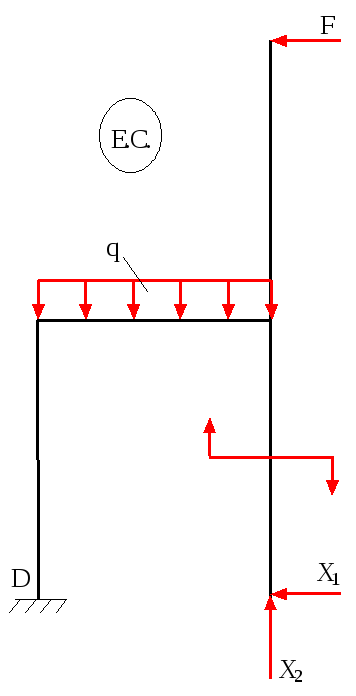
Рис.10.2
Для знаходження невідомих складаємо систему канонічних рівнянь:
11X1+12X2+1F=0
21X1+22X2+2F=0
Число рівнянь стільки, скільки невідомих X1 і X2.
Перший індекс при коефіцієнтах показує напрямок переміщення, другий – причину переміщення.
Коефіцієнти і вільні члени рівнянь визначаються по формулі Мора:
![]()
Замінимо
інтегрування перемноженням епюр по
правилу Верещагіна (або Симпсона-Карнаухова).
Для цього побудуємо епюри згинаючих
моментів від одиничних сил
![]() і
і![]() ,
а також епюру МF
від зовнішнього навантаження.
,
а також епюру МF
від зовнішнього навантаження.
Епюра
згинаючих моментів від
![]() і
і![]() (рис.10.3).
(рис.10.3).
а) б)
б)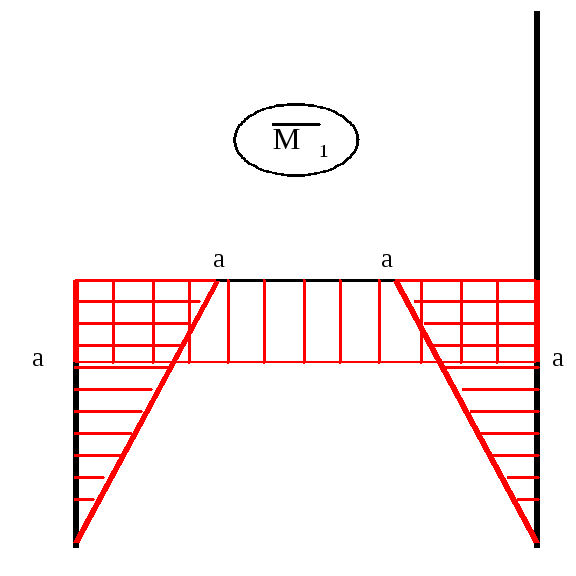
в)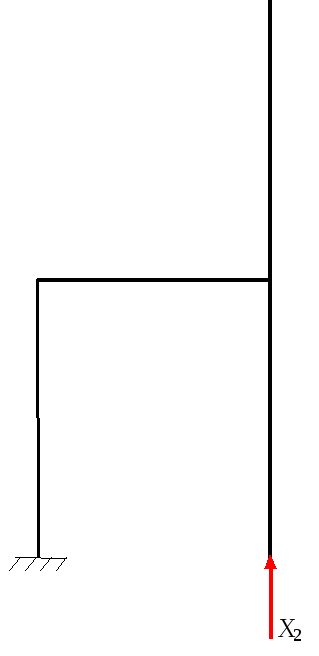 г)
г)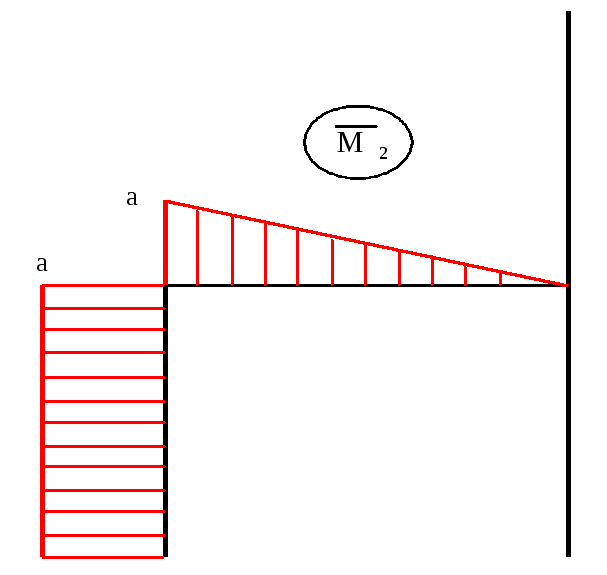
Рис.10.3
Будуємо епюри згинаючих моментів від зовнішнього навантаження (рис.10.4).
а)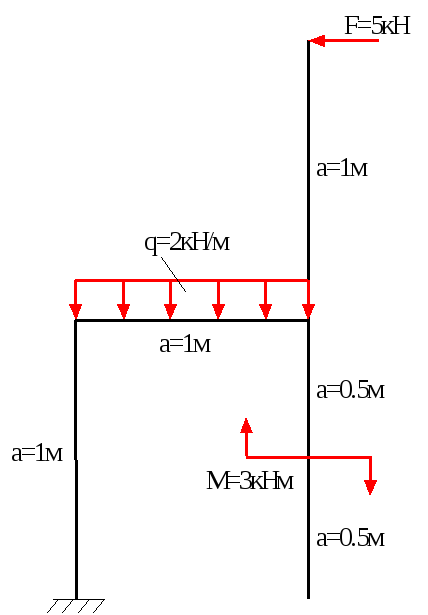 б)
б)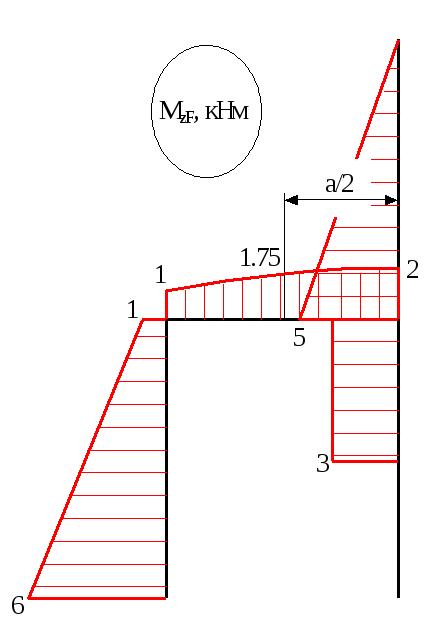
Рис.10.4
Визначаємо коефіцієнти канонічних рівнянь:
![]() ,
,
![]() ,
,
![]() .
.
Вантажні члени рівнянь:
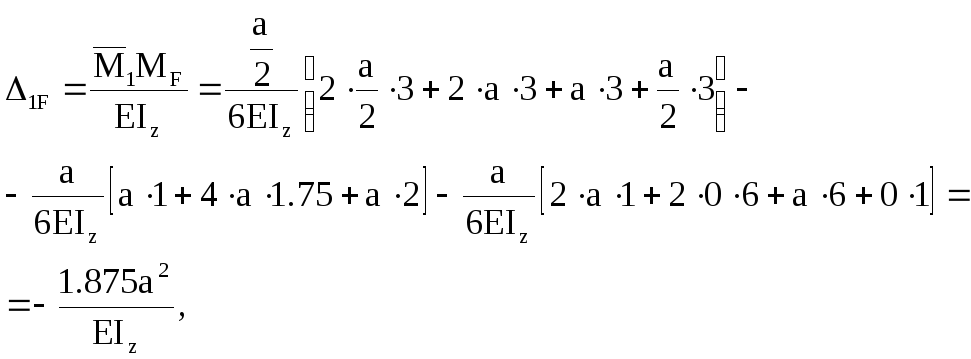
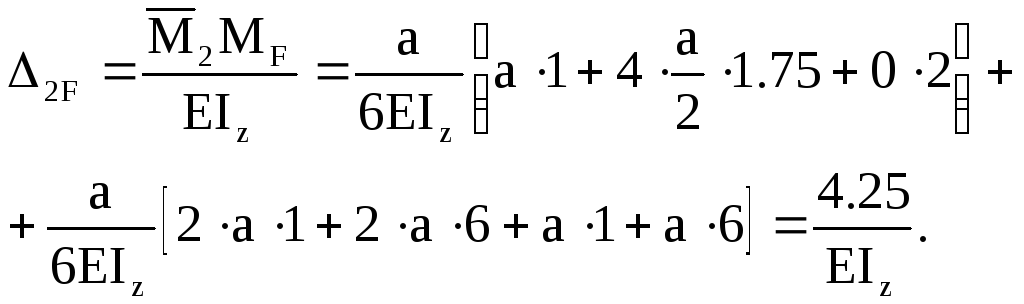
Підставляємо замість а=1м, отримаємо:
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
Підставляємо
в рівняння і скорочуючи на
![]() ,
запишемо:
,
запишемо:
![]() ,
,
![]() .
.
Розв’язуючи спільно систему рівнянь, знайдемо:
X1=-1.43кН, X2=-4.26кН.
Знак мінус говорить про те, що напрямки реакцій X1 і X2 протилежні вибраним.
Будуємо сумарну епюру згинаючих моментів Mz, а також епюри поперечних сил Qy і повздовжніх сил N (рис.10.5).
Деформаційна перевірка
Деформаційна перевірка виражає суть канонічних рівнянь, тобто