Файл: 3.doc

Переріз 3-3 (0X150см)

Y=0; N₃-G₃+F₂-G₂-G₁-F₁=0,

,

N₃(x=0)=A₃0-F₂+A₂b+A₁a+F₁=78.510^-3600-4000+

+78.510^-340100+78.510^-320100+2000=-1529Н,

N₃(x=150)=A₃150-F₂+A₂b+A₁a+F₁=78.510^-360150-4000+

+78.510^-340100+78.510^-320100+2000=-822.5Н.

Переріз 4-4 (0X50см)

Y=0; N₄-G₄-F₃-G₃+F₂-G₂-G₁-F₁=0,

,

; A₄=A₃-A_отв=60-19.6=40.4см²,

N₄(x=0)=A₄0+F₃+A₃c-F₂+A₂b+A₁a+F₁=

=78.510^-340.40+3000+78.510^-360150-4000+78.510^-340100+

+78.510^-320100+2000=2177.5Н,

N₄(x=50)=A₄50+F₃+A₃с-F₂+A₂b+A₁a+F₁=

=78.510^-340.450+3000+78.510^-360150-4000+78.510^-340100+

+78.510^-320100+2000=2336Н.

Епюра осьових зусиль є графік розподілу осьових зусиль по довжині стержня (рис.1.2,е). В масштабі по вертикалі відкладається довжина стержня в сантиметрах, по горизонталі – осьові зусилля N в кілограмах.

2. Епюри крутних моментів

Деформація кручення найбільш розповсюджена в валах. Якщо навантаження на прямолінійний стержень (вал) складається тільки з моментів М_к, площини яких перпендикулярні до осі стержня, то з шести зусиль і моментів в будь-якому перерізі залишається тільки крутний момент М_кр.

Внутрішній момент М_кр виражається через зовнішні М_к: М_кр в перерізі дорівнює сумі зовнішніх моментів М_к, розташованих по одну сторону від перерізу. Якщо стержень (вал) обертається рівномірно, то алгебраїчна сума всіх М_к дорівнює нулю. Тому результат буде отримано один і той же, чи будемо при розрахунку М_кр брати суму моментів М_к, розташованих зліва чи справа від перерізу.

Крутний момент М_кр вважається додатним, якщо при спостеріганні з торця вздовж осі частини, яка розглядається, він намагається обертати переріз за годинниковою стрілкою (рис.2.1).

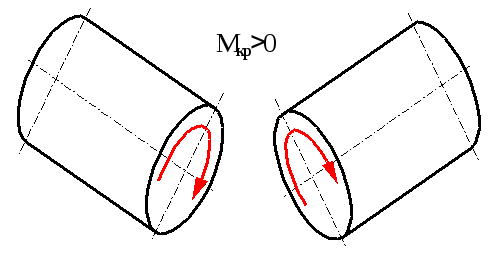
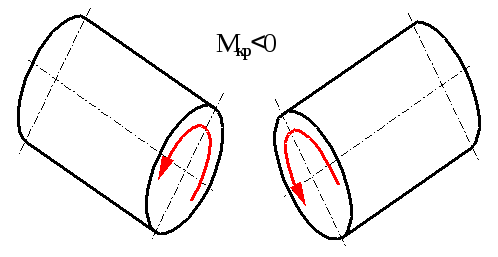
Рис.2.1

Приклад

Побудувати епюри крутних моментів для вала з насадженими на нього шківами (рис.2.2), якщо: М=40кНм; М₁=М; М₂=2М; М₃=2.5М; М₄=1.5М; m=100кНм/м; а=0.6м

При розрахунках на міцність і жорсткість знак крутного моменту не грає ніякої ролі, але для зручності побудови епюр пропонується вважати крутний момент додатнім, якщо дивлячись в торець відсіченої частини бруса цей момент є направленим за годинниковою стрілкою.

Величина М₀ визначається з умови рівноваги вала, знак приймається по вище приведеному правилу, причому дивитися будемо з правого торця вала. Напрямок обертання М₀ орієнтовно показуємо за годинниковою стрілкою.

М=0 М₁+М₀-М₂+ma-М₃+М₄=0,

М₀=-М₁+М₂-ma+М₃-М₄=-40+80-1000.6+100-60=20кНм.

Крутний момент М₀ отримано зі знаком плюс, таким чином напрямок визначили правильно. Якщо М₀ з умови рівноваги виявиться відємним, то необхідно змінити його напрямок на протилежний і в подальшому знак мінус не враховувати.

Для визначення величини крутних моментів вал розбивається на ділянки між суміжними шківами, виконуються переріз на кожній ділянці, одна частина системи відкидається, її дія заміняється М_кр, величина якого знаходиться з умови рівноваги частини, яка залишилася. Розглянемо переріз 1-1 (рис.2.2,б). Відкинута права частина, напрямок М_кр1 необхідно приймати за годинниковою стрілкою, якщо дивитися в торець відсіченої частини вала.

Переріз 1-1

М=0, М₁+М_кр1=0,

М_кр1=-М₁=-40кНм.

Аналогічно розглядаємо інші перерізи, складаючи рівняння рівноваги для лівих частин вала.

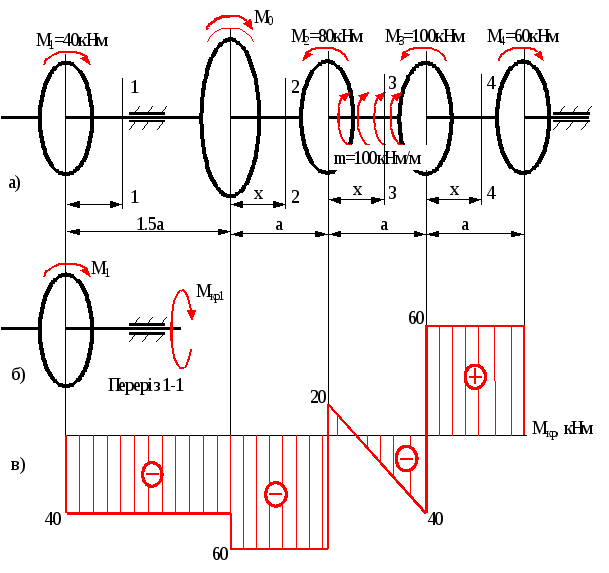
Рис.2.2

Переріз 2-2

М=0, М₁+М₀+М_кр2=0,

М_кр2=-М₁-М₀=-40-20=-60кНм.

Переріз 3-3 (0xa)

М=0, М₁+М₀-М₂+mx+М_кр3=0,

М_кр3(x=0)=-М₁-М₀+М₂-m0=-40-20+80-1000=20кНм,

М_кр3(x=a)=-М₁-М₀+М₂-ma=-40-20+80-1000.6=-40кНм.

Переріз 4-4

М=0 М₁+М₀-М₂+ma-M₃+М_кр4=0,

М_кр4=-М₁-М₀+М₂-ma+М₃=-40-20+80-1000.6+100=60кНм.

Епюрою крутних моментів називається графік розподілу моментів по довжині вала. В масштабі по горизонталі відкладаються довжина вала в метрах, по вертикалі – крутні моменти в кНм. Вверх відкладаються додатні моменти, вниз - від’ємні (рис.2.2,в).

3. Побудова епюр внутрішніх силових факторів при згині балок

Згином вважається такий вид деформації, при якому в поперечних перерізах бруса виникають згинаючі моменти.

Якщо згинаючий момент є єдиним силовим фактором в перерізі бруса, то згин називають чистим.

В більшості випадків в поперечних перерізах бруса наряду з згинаючим моментом М виникає і поперечна сила Q. В цьому випадку згин називається поперечним.

Брус, який працює в основному на згин називається балкою.

Побудову епюр Q і М починають з визначення повної системи навантажень, в які входять як задані сили, так і реакції опор, тому, при необхідності, спочатку визначають реакції опор. Визначивши реакції опор і зробивши перевірку правильності їх визначення, балку розбивають на ділянки. При цьому керуються правилом, що межами ділянок є: точки прикладення зосереджених сил, зосереджених моментів, а також місця різкої зміни інтенсивності розподіленого навантаження.

Далі, використовуючи метод перерізів, будують епюри Q і М на кожні з ділянок балки. З методу перерізів випливає, що:

1. поперечна сила Q в перерізі балки чисельно дорівнює алгебраїчній сумі проекцій на вертикальну ось перерізу всіх сил, які діють по одну сторону від нього;

2. згинаючий момент М в перерізі балки чисельно дорівнює алгебраїчній сумі моментів відносно поперечної осі перерізу, який розглядається, всіх сил, які розташовані по одну сторону від цього перерізу.

При цьому вводяться наступні правила знаків для Q і М. Для Q: навантаження, яке намагається повернути відсічену частину балки відносно перерізу, який розглядається, за годинникової стрілкою, дасть у виразі для Q додатній доданок. Графічно це правило можна зобразити так

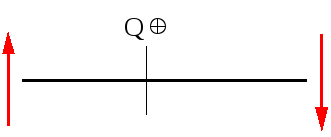
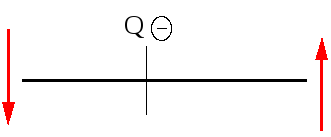
Рис.3.1

Для М: навантаження, яке створює відносно перерізу, який розглядається, момент, який згинає балку опуклістю вниз і, який створює стиск в верхніх волокнах, дасть у виразі для М додатній доданок. Графічно це правило зображають так

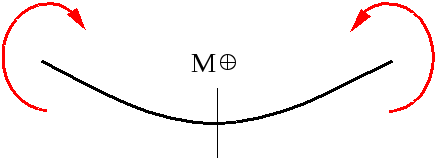
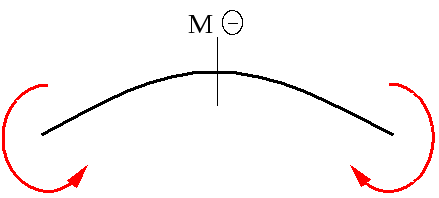
Рис.3.2

Для контролю правильності побудови епюр використовують диференціальні залежності при згині (теореми Журавського):

; ;,

а точніше сказати слідства, які витікають з цих залежностей:

1. Якщо на ділянці балки відсутнє розподілене навантаження, тобто q=0, то тут Q=const, а М змінюється по лінійні залежності;

2. Якщо на ділянці балки діє рівномірно розподілене навантаження інтенсивністю q, то функція Q буде лінійною, а М – квадратичною. При цьому опуклість параболи буде направлена назустріч q;

3. В точках, де Q=0, на епюрі М має місце екстремум;

4. В точках прикладення до балки зосереджених сил епюра Q зазнає скачок на величину зовнішньої сили, а на епюрі М виникає відповідний злом (розрив в похідні);

5. В точках прикладення до балки зосереджених моментів епюра М зазнає скачок на величину зовнішнього моменту.

Приклад 1

Для заданої консольної балки (рис.3.3) побудувати епюри поперечних сил та згинаючих моментів, якщо: а=1.5м, q=15кН/м, М=20кНм, F=10кН.

Розрахункова схема консольної балки креслиться в масштабі і розбивається на ділянки. За ділянку балки приймається відстань між суміжними навантаженнями. Дана балка розбивається на три ділянки.

Реакції опор в місці защемлення для консольної балки не визначаються, проводять перерізи на кожні ділянці і розглядають праву частину балки, тобто частину яка відноситься до вільного кінця.

Епюрою поперечної сили називається графік зміни поперечної сили по довжині. Поперечна сила при плоскому згині чисельно дорівнює алгебраїчні сумі зовнішніх сил, які знаходяться по одну сторону від перерізу. Поперечна сила приймається додатною, якщо вона намагається обертати частину балки яка розглядається за годинникової стрілкою, і відємною – при обертанні проти годинникової стрілки.

Епюрою згинаючих моментів називається графік зміни згинаючих моментів по довжині балки. Згинаючий момент чисельно дорівнює сумі моментів зовнішніх сил, які лежать по одну сторону від перерізу, відносно центра ваги перерізу. Згинаючий момент додатній, якщо він стискає верхні волокна балки, і відємний, коли стискає нижні волокна балки. Розглянемо рівновагу частини балки, яка відсічена перерізом 1-1