Файл: 3.doc

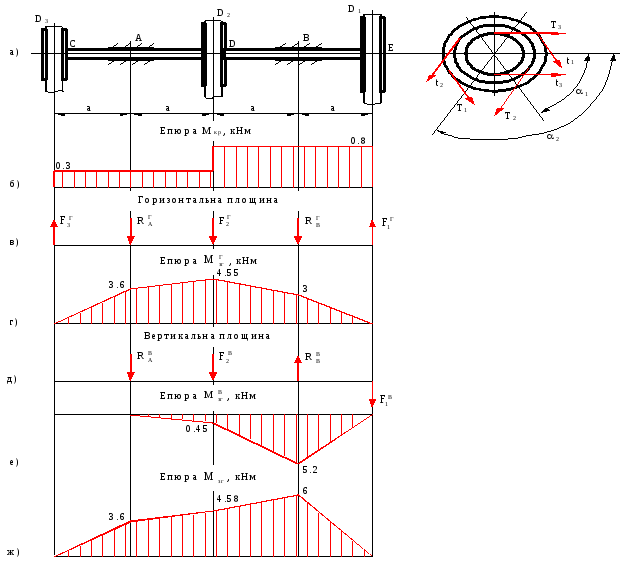
Рис.8.2

Визначаємо сили, які передаються на вал від натягу пасів:

F₁=3t₁=32=6кН,

,

F₃=3t₃=31.2=3.6кН.

На схемі в аксонометрії показуємо розташування зусиль, які діють на вал і розкладаємо їх на горизонтальні і вертикальні складові (рис.8.1,а).

Визначаємо величину складових, які діють в горизонтальні (ось Z) площині:

,

,

.

В вертикальній площині:

По отриманим даним будуємо епюру згинаючих моментів від дії сил в горизонтальні і вертикальні площині (рис.8.2,г,е).

Будуємо сумарну епюру згинаючих моментів. Для цього знаходимо сумарні згинаючі моменти в характерних перерізах вала, як геометричну суму згинаючих моментів в вертикальній і горизонтальній площинах.

,

,

.

По епюрам М_кр і М_зг бачимо, що небезпечний переріз буде в точці В, так як в цьому перерізі найбільший згинаючий момент (М_зг=6кНм) і найбільший крутний момент (М_кр=0.8кНм).

Приведений момент по ІІІ теорії міцності:

.

Визначаємо діаметр валу, виходячи з умови міцності для небезпечного перерізу:

. (8.1)

Момент опору для круглого перерізу:

. (8.2)

Підставляючи (8.2) в (8.1), отримаємо:

.

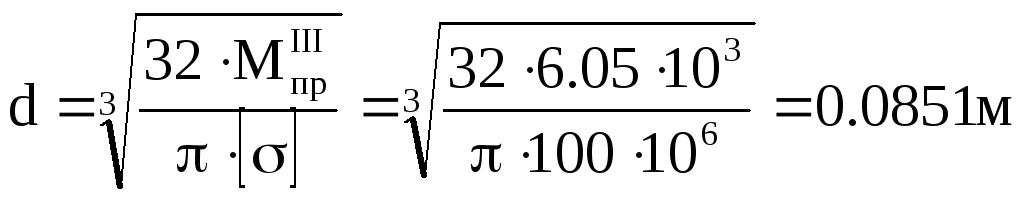Приймаємо d=90мм.

9. Визначення переміщень в пружних системах

Найбільш загальною для визначення переміщень в стержнях є формула Мора. При наявності всіх шести компонентів внутрішніх зусиль, формула має вид

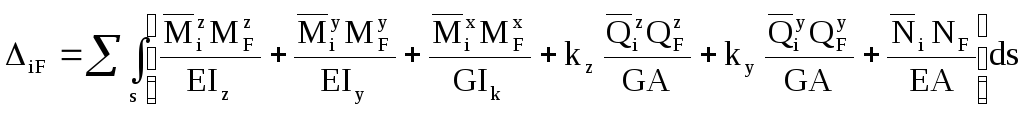(9.1)

де k_y, k_z – коефіцієнти, які залежать від форми перерізу

В більшості випадків при визначенні переміщень в балках, рамах і арках по методу Мора в формулі (9.1) можна знехтувати впливом повздовжніх деформацій і зсуву, враховуючи тільки переміщення, які викликаються згином. Тоді формула (9.1) для плоскої системи може бути записана наступним чином:

.

Порядок визначення переміщень по методу Мора.

1. Будується допоміжна система і навантажується одиничним навантаженням в точці, де необхідно визначити переміщення. При визначенні лінійних переміщень в заданому напрямку прикладається одинична сила, при визначенні кутових переміщень – одиничний момент.

2. Для кожної ділянки системи виписується вираз силових факторів в довільному перерізі заданої (M_F, N_F, Q_F) і допоміжної (,,) систем.

3. Розраховуються по всім ділянкам системи інтеграли Мора.

4. Якщо розраховане переміщення має додатній знак, то це значить, що його напрямок співпадає з напрямком одиничної сили. Від’ємний знак вказує на те, що дійсне переміщення протилежне напрямку одиничної сили.

Інтеграл Мора для випадку, коли епюра від заданого навантаження має довільний, а від одиничного – прямолінійний обрис (рис.9.1), виявилось зручним визначати графоаналітичним способом, запропонованим А.Н.Верещагіним.

Рис.9.1

Загальна формула переміщень для систем, які складаються з прямолінійних елементів запишеться у вигляді

де  - площа епюри M_F від зовнішнього навантаження;

- ордината епюри від одиничного навантаження під центром ваги епюриM_F.

Це і є формула Верещагіна. Розрахунок по цій формулі виконується по ділянкам, на кожній з яких прямолінійна епюра повинна бути без переломів (рис.9.2).

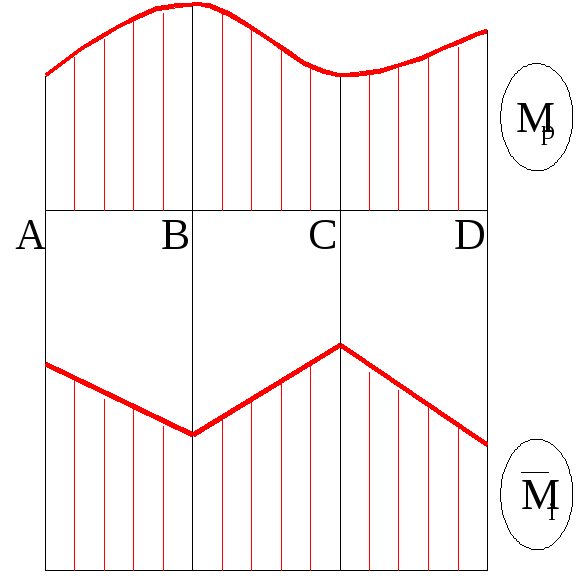
Рис.9.2

У випадку, коли епюри M_F окреслені по квадратній параболі або прямій, а - по прямій, ефективно застосуванняформули Сімпсона-Корноухова

,

де ,- крайні ліві ординати епюр, які перемножуються,

,- середні ординати епюр, які перемножуються,

, - крайні праві ординати епюр, які перемножуються.

Таблиця 9.1. Вирази інтегралу Мора для різних сполучень епюріM_F (l – основа площі епюри)

Приклад

Визначити прогин перерізу А і кут повороту перерізу В для заданої консольної балки (рис.9.3,а).

Дано: l=3м; q=4т/м; ; М=ql²; Е=210⁵ МПа (додаток 4).

Двутавр №40: I_z=19062см⁴ (додаток 6);

1.Метод Мора.

Розрахункову схему балки викреслюють в масштабі (рис.9.3,а) і розбивають на ділянки АВ, ВС, CD.

Прогин (переріз А) балки визначають методом Мора. Поставлену задачу розв’язують у певні послідовності.

1. Будують допоміжну систему, яку навантажують одиничним навантаженням в точці, де необхідно визначити переміщення. В нашому прикладі визначають лінійне переміщення, тому в точці А прикладають одиничну силу (рис.9.3,б).

2. Для кожної ділянки системи виписують вирази силових факторів в довільному перерізі заданої М_F і допоміжної систем:

Ділянка АВ:

M_F1=0,

Ділянка ВC:

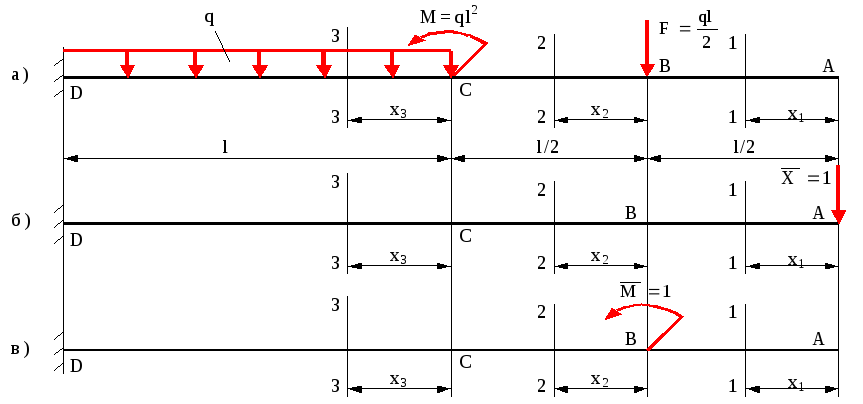
Рис.9.3

Ділянка CD: 0x₃l

Визначають лінійне переміщення перерізу А за допомогою інтеграла Мора (по ділянках в межах всієї консольної балки).

На ділянці АВ інтеграл Мора дорівнює нулю, так як згинаючий момент від зовнішніх навантажень на цій ділянці дорівнює нулю. Розраховане лінійне переміщення має від’ємний знак, отже його напрямок не співпадає з напрямком одиничної сили.

Знаходимо кут повороту перерізу В. Для цього в перерізі В прикладаємо одиничний момент і запишемо вирази дляM_Fi і