ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 289
Скачиваний: 0
СОДЕРЖАНИЕ
5. Геометричні характеристики поперечних перерізів бруса.
Зміна моментів інерції при повороті осей. Головні осі і головні моменти інерції
6. Розрахунок на міцність при згині
7. Позацентровий розтяг (стиск) стержня високої жорсткості
9. Визначення переміщень в пружних системах
10. Статично невизначені системи
11. Розрахунок стиснутих стержнів на стійкість
12. Наближений розрахунок на удар
Механічні характеристики вуглецевих конструкційних сталей
Додаток 2 Механічні характеристики чавуну
Додаток 3 Орієнтовні значення основних допустимих напруг на розтяг і стиск
Переріз 1-1 (0Xа)

Рівняння поперечної сили:
Qy=-F=-10кН.
В рівняння поперечної сили не ввійшла координата x, відповідно маємо рівняння прямої паралельної осі X.
Проводиться горизонтальна лінія, паралельна осі балки і в масштабі яка відповідає довжині балки. По вертикалі відкладається в масштабі величина поперечної сили. Додатні значення поперечної сили відкладаються вверх, від’ємні – вниз.
Рівняння згинаючого моменту:
Mz=Fx.
В рівняння згинаючого моменту x входить в перші степені, відповідно маємо рівняння прямої.
Mz(x=0)=0,
Mz(x=a)=Fa=101.5=15кНм.
Проводиться горизонтальна лінія, паралельна осі і в масштабі яка відповідає довжині балки. По вертикалі відкладається згинаючий момент: від’ємний – вниз, додатній – вверх. В загальному випадку масштаб Qy і Mz приймається неоднаковим.
Переріз 2-2 (0Xа)
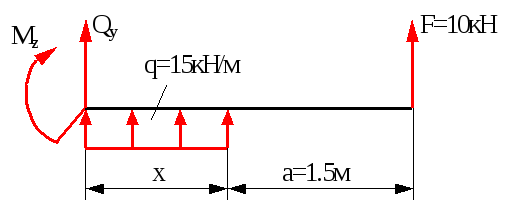
Рівняння поперечної сили:
Qy=-F-qx.
Текуча координата входить в рівняння поперечної сили в перші степені, відповідно маємо рівняння прямої лінії. Для її побудови визначаються дві точки.
Qy(x=0)=-F=-10кН,
Qy(x=a)=-F-qa=-10-151.5=-32.5кН.
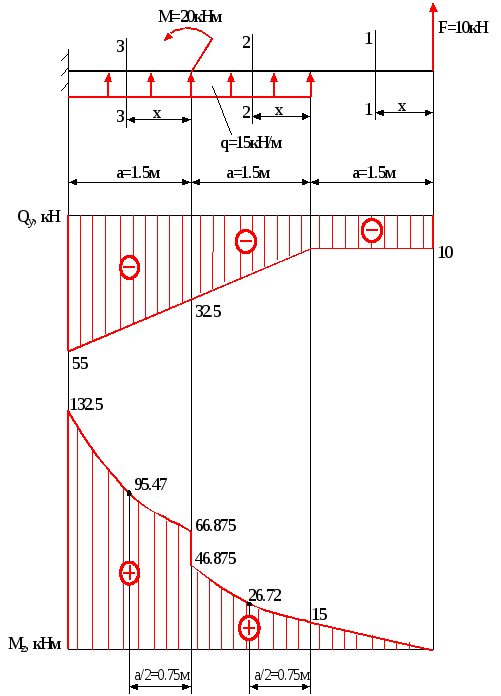
Рис.3.3
Рівняння згинаючого моменту:
![]() .
.
Отримано рівняння кривої лінії (параболи), тому що x входить у другій степені. Для орієнтовної побудови кривої необхідно мати хоча б три точки.
Mz(x=0)=Fa=101.5=15кНм,
![]() ,
,
 .
.
Переріз 3-3 (0Xа)
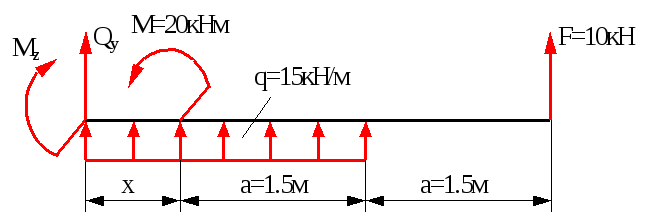
Qy=-F-q(a+x),
Qy(x=0)=-F-qa=-10-151.5=-32.5кН,
Qy(x=a)=-F-q(a+a)=-10-15(1.5+1.5)=-55кН,
![]() ,
,
![]() ,
,


Приклад 2
Для заданої балки (рис.3.4) побудувати епюри поперечних сил і згинаючих моментів, якщо: а=2м, М=25кНм, F1=15кН, F2=25кН.
В точках А і В виникають реактивні сили RА і RВ. Горизонтальна складова в шарнірно-нерухомі опорі А дорівнює нулю, тому що немає зовнішніх сил, які діють в горизонтальному напрямку.
З умови рівноваги балки визначаються реакції.
Рівняння статики:
МА=0, М-F1а- F2(а+а) +RВ(а+а+а)=0,
![]() ,
,
МВ=0, -RА(а+а+а)+М+F1(а+а)+F2а =0,
![]() .
.
Перевірка:
Y=0, RА+RB-F1-F2=22.5+17.5-15-25=0.
Розрахункова схема балки креслиться в масштабі і розбивається на ділянки. За ділянку балки приймається відстань між суміжними навантаженнями. Дана балка розбивається на три ділянки. Проводяться перерізи на кожні ділянці і записуються рівняння поперечної сили та згинаючого моменту.
Переріз 1-1 (0Xа)

Qy=RA=22.5кН,
Mz=RAx-M,
Mz(x=0)=-M=-25кНм,
Mz(x=a)=RAа-M=22.52-25=20кНм.
Переріз 2-2 (0xа)

Qy=-RВ=-17.5кН,
Mz=RВx,
Mz(x=0)=0,
Mz(x=a)=RВа=17.52=35кНм.

Рис.3.4
Переріз 3-3 (0xа)
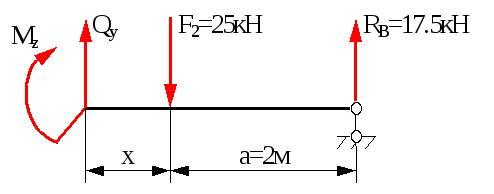
Qy=-RВ+F2=-17.5+25=7.5кН,
Mz=RВ(a+x)-F2x,
Mz(x=0)=RВa=17.52=35кНм,
Mz(x=a)=RВ(a+а)-F2а =17.5(2+2)-252=20кНм.
Приклад 3
Для заданої балки (рис.3.5) побудувати епюри поперечних сил і згинаючих моментів, якщо: а=1м, q=10кН/м, М=30кНм, F=20кН.
Рівняння статики:
МА=0, Fа-М-q3а(а+1.5а)+RВ(а+3а)=0,
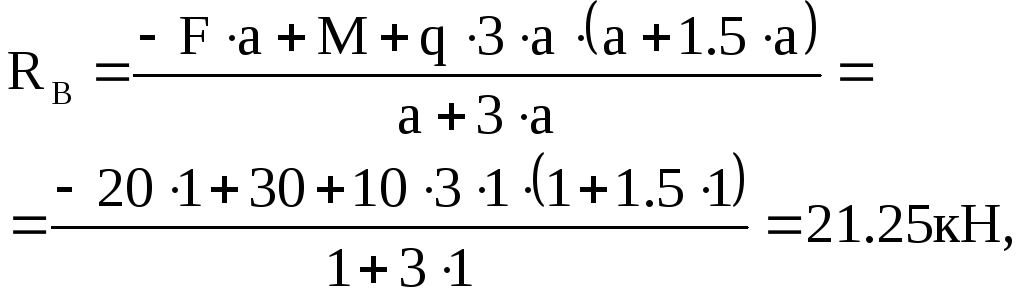
МВ=0 F(а+а+3а)-RА(а+3а)-М+q3а1.5а=0,
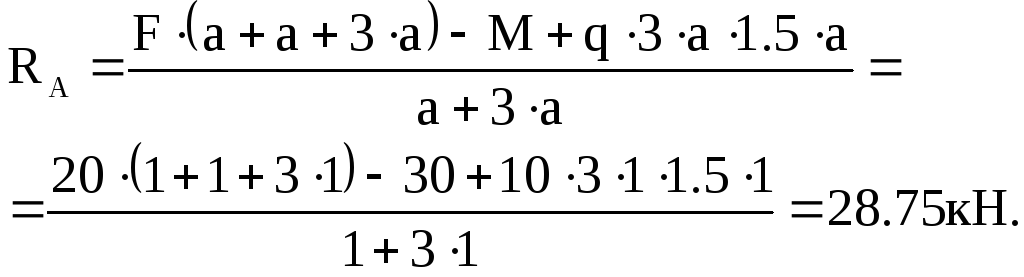
Перевірка:
Y=0, -F+RА-q3а+RB=-20+28.75-1031+21.25=0.
Переріз 1-1 (0xа)

Qy=-F=-20кН,
Mz=-Fx,
Mz(x=0)=0,
Mz(x=a)=-Fa=-201=-20кНм.
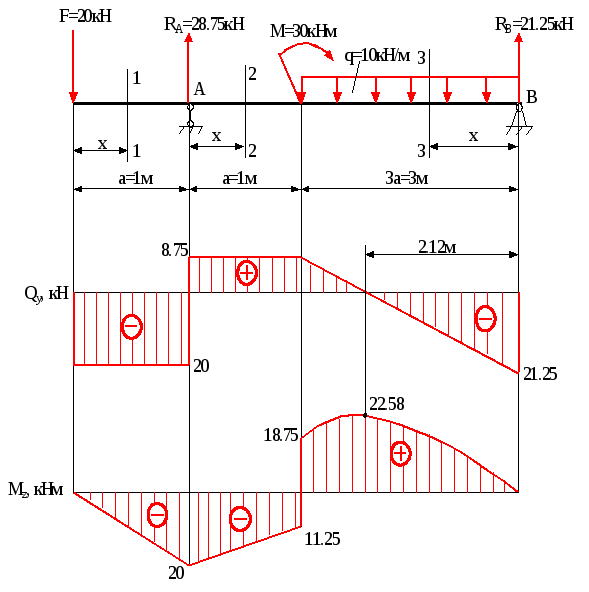 Рис.3.5
Рис.3.5
Переріз 2-2 (0xа)

Qy=-F+RA=-20+28.75=8.75кН,
Mz=-F(a+x)+RAx,
Mz(x=0)=-Fa=-201=-20кНм,
Mz(x=a)=-F(a+а)+RAa=-20(1+1)+28.751=-11.25кНм.
Переріз 3-3 (0x3а)

Qy=-RB+qx,
Qy(x=0)=-RB=-21.25кН,
Qy(x=3a)=-RB+q3a=-21.25+1031=8.75кН,
![]() ,
,
Mz(x=0)=0,
![]() .
.
Для визначення максимуму згинаючого моменту використовується диференціальна залежність між Qy і Mz.
![]()
Функція має максимум, коли перша похідна дорівнює нулю, а поперечна сила міняє знак з “+” на “-”. Значення поперечної сили для третього перерізу прирівнюємо до нуля і визначаємо значення x, при якому Qy=0
-RB+qx=0,
![]() .
.
Знайдене значення x підставляємо в рівняння згинаючого моменту
![]() .
.
Таким чином, на відстані 2.125м від точки В згинаючий момент має максимум і дорівнює 22.58кНм.
Приклад 4
Для заданої рами (рис.3.6) побудувати епюри поперечних сил і згинаючих моментів, якщо: а=2.5м, q=15кН/м, М=15кНм, F1=20кН, F2=30кН.
Рівняння статики:
МА=0, ![]() ,
,
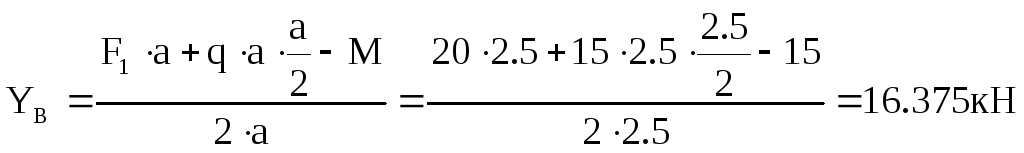 ,
,
Y=0, YB-qа+F2-YA=0,
YA=YB-qа+F2=16.375-152.5+30=8.875кН,
X=0, -F1+XA=0,
XA=F1=20кН.

Рис.3.6
Переріз 1-1 (0Xа)

Qy=YB=16.375кН.
Величина осьових зусиль визначається з умови рівноваги відсіченої частини
X=0, -N+F1=0,
N=F1=20кН,
Mz=YBx,
Mz(x=0)=0,
Mz(x=a)=YBa=16.3752.5=40.94кНм.
а)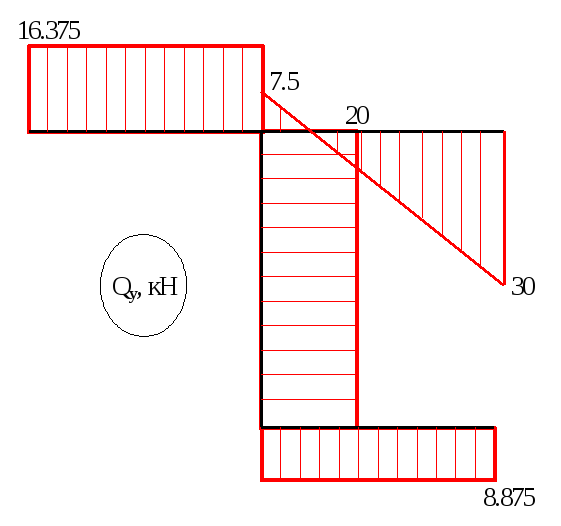 б)
б)
в)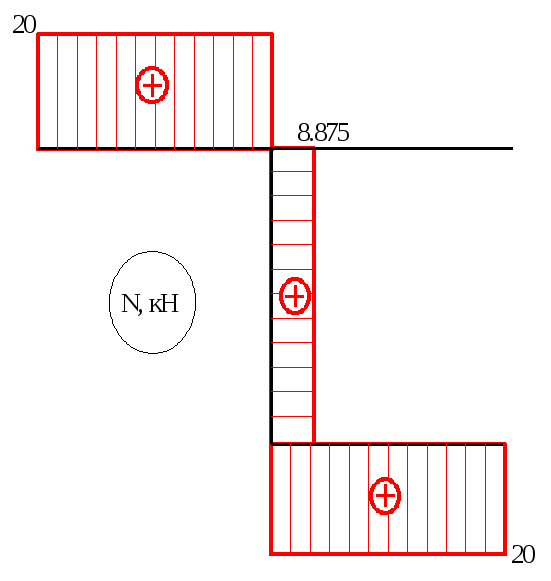
Рис.3.7
Переріз 2-2 (0xа)
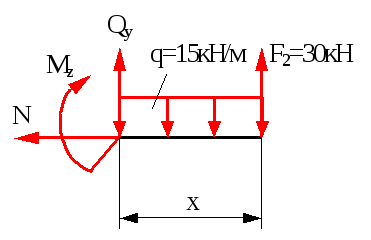
Qy=-F2+qx,
Qy(x=0)=-F2=-30кН,
Qy(x=a)=-F2+qa=-30+152.5=7.5кН,
N=0,
![]() ,
,
Mz(x=0)=0,
![]() ,
,
Qy=-F2+qx=0;
![]() ,
,
![]() .
.
Переріз 3-3 (0xа)
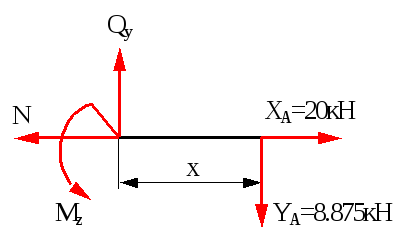
Qy=YA=8.875кН,
N=XA=20кН,
Mz=YAx,
Mz(x=0)=0,
Mz(x=a)=YAa=8.8752.5=22.19кНм.
Переріз 4-4 (0xа)
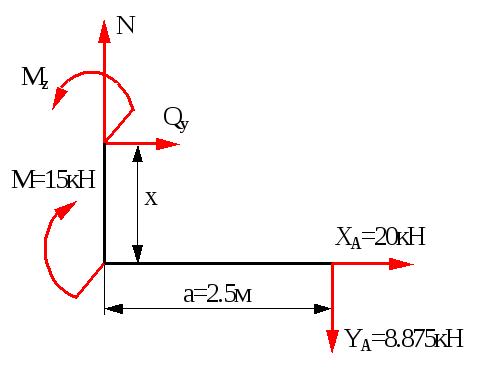
Qy=-XA=-20кН,
N=YA=8.875кН,
Mz=YAa-XAx+M,
Mz(x=0)=YAa+M=8.8752.5+15=37.19кН,
Mz(x=a)=YAa-XAa+M =8.8752.5-202.5+15=-12.81кНм.
4. Статично невизначені стержневі системи
На практиці зустрічаються системи, для визначення внутрішніх зусиль в яких рівнянь статики виявляється недостатньо. Такі системи називають статично невизначеними. В цих системах число накладених зв’язків більше, чим це необхідно для їх кінематичної незмінності, тобто для їх рівноваги. Іншими словами, всі с.н.с. мають додаткові або “зайві” з точки зору кінематичної незмінності зв’язки, постановка яких диктується умовами міцності або жорсткості.