ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 293
Скачиваний: 0
СОДЕРЖАНИЕ
5. Геометричні характеристики поперечних перерізів бруса.
Зміна моментів інерції при повороті осей. Головні осі і головні моменти інерції
6. Розрахунок на міцність при згині
7. Позацентровий розтяг (стиск) стержня високої жорсткості
9. Визначення переміщень в пружних системах
10. Статично невизначені системи
11. Розрахунок стиснутих стержнів на стійкість
12. Наближений розрахунок на удар
Механічні характеристики вуглецевих конструкційних сталей
Додаток 2 Механічні характеристики чавуну
Додаток 3 Орієнтовні значення основних допустимих напруг на розтяг і стиск
Мzmax=200кНм=200103Нм; []=160МПа=160106Па,
![]() .
.
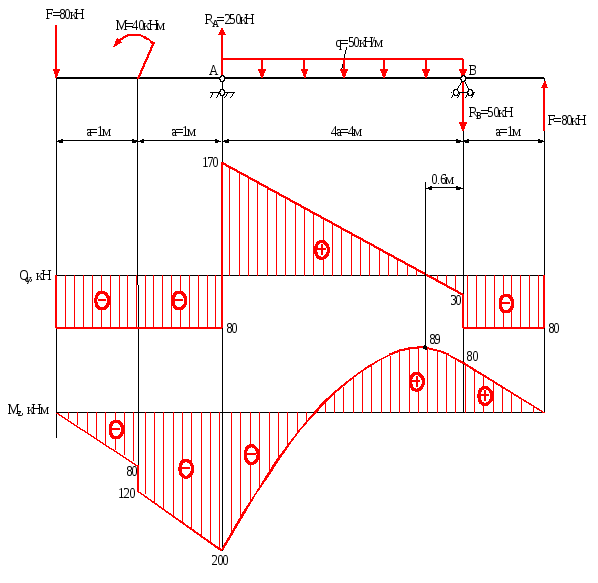
Рис.6.1
Двутавр
Відповідно до ДЕСТ 8239-72 (додаток 6) приймається двутавр №45 з наступними характеристиками: Iz=27696см4, Wz=1231см3, Sz=708см3, A1=84.7см2, h=45см, b=16см, t=1.42см, d=0.9см.
Дійсні напруження
![]() .
.
Перенапруження
![]() 5.
5.
Прямокутник
![]() ;
h=2b;
;
h=2b;
![]() ;
;
![]() ;
h=2b=212.3=24.6см.
;
h=2b=212.3=24.6см.
Площа прямокутного перерізу
А2=bh=12.324.6=303.3см2.
Круглий переріз
![]() ;
;
![]() .
.
Площа круглого перерізу
![]()
Відношення ваги погонного метра балки прямокутного і круглого поперечного перерізу до погонного метра балки двотаврового перерізу дорівнює
А1:А2:А3=1:3.58:5.06.
Епюри нормальних і дотичних напружень для двотаврового перерізу показані на рис.6.2 Нормальні напруження мають максимум в крайніх верхніх і нижніх волокнах, а дотичні – в центральних волокнах двутавра. При повній перевірці міцності, коли враховується дія і нормальних і дотичних напружень, за небезпечну точку приймається точка 2, де близькі до максимуму нормальні напруження і мають значну величину дотичні.
З рис.6.1 видно, що небезпечним перерізом буде переріз в точці А, де згинаючий момент і поперечна сила мають максимальні значення.
Таким чином дані для розрахунку: Мzmax=200кНм; Qymax=170кН
Нормальні напруження в точці 2
![]()
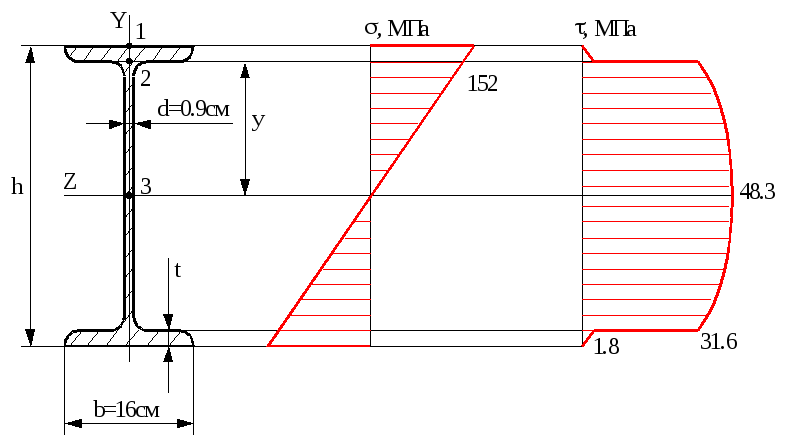 Рис.6.2
Рис.6.2
Відстань y від осі Z до точки 2 визначається з рис.6.2
![]()
Дотичні напруження в точці 3
![]()
Статичний момент полки відносно осі Z
![]()
де Аполки=bt – площа поперечного перерізу полки;
![]() - відстань до центру ваги полки.
- відстань до центру ваги полки.
Дотичні напруження в точці 2
![]()
![]()
Еквівалентне напруження визначається по четвертій теорії міцності
![]()
Перенапруження
![]() 5.
5.
7. Позацентровий розтяг (стиск) стержня високої жорсткості
Позацентровим розтягом (стиском) називається такий випадок дії сили на брус, коли сила, паралельна осі бруса, прикладена не в центрі ваги перерізу.
Враховуючи велику жорсткість бруса, можна застосувати принцип незалежності дій сил і розглядати позацентровий розтяг (стиск) як спільну дію косого згину, який викликається моментом FAO і центрального розтягу (стиску) силою F (рис.7.1).
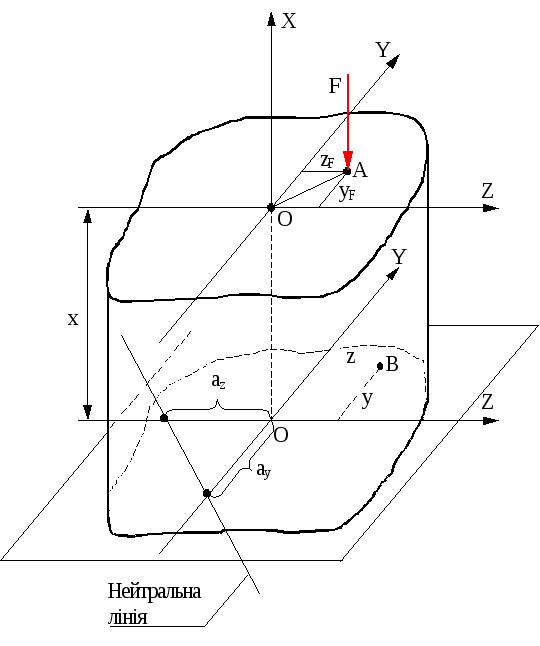
Рис.7.1
Найбільший практичний інтерес представляють задачі на позацентровий розтяг (стиск), особливо у випадку, якщо допустимі значення напружень розтягу і стиску матеріалу різні. Прикладами таких матеріалів можуть бути чавун, бетон, цегляна і камінна кладка і т.д.
Нормальні напруження в довільні точці перерізу при позацентровому розтягу (стиску) можна визначити по формулі
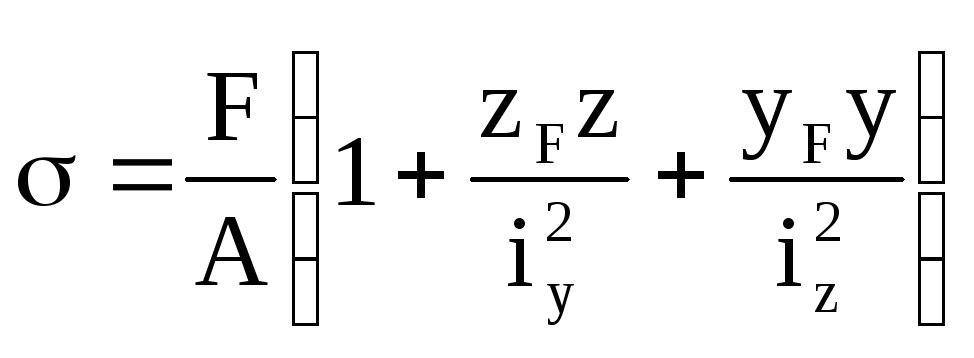 , (7.1)
, (7.1)
де F – величина позацентрово прикладеної сили;
А – площа поперечного перерізу бруса;
zF, yF – координати точки прикладення сили F (т.А);
z, y – координати точки, де визначають напруження (т.В);
![]() ,
,![]() - радіуси інерції перерізу.
- радіуси інерції перерізу.
Необхідно відмітити, що всі координати і радіуси інерції визначають відносно головних центральних осей. Якщо напрямок цих осей вибрати таким, щоб точка прикладення сили лежала в першому квадранті (див.рис.7.1), то знаки доданків в формулі (7.1) будуть співпадати з знаками z, y точки, де визначають напруження.
Можна
також використати наступне правило
знаків при розрахунку напружень по
формулы (7.1). Знаки А,
![]() і
і![]() завжди позитивні. СилаF
приймається додатною (F>0)
при розтягу і відємною
(F<0)
при стиску. Координати z,y,zF
і yF
беруться зі своїми знаками.
завжди позитивні. СилаF
приймається додатною (F>0)
при розтягу і відємною
(F<0)
при стиску. Координати z,y,zF
і yF
беруться зі своїми знаками.
Розрахунки на міцність виконують по нормальним напруженням, так як дотичні напруження в поперечних перерізах відсутні. Як і при косому згині, величина нормальних напружень прямопропорційна відстані точки від нейтральної лінії, і для визначення небезпечної точки треба провести прямі, паралельні нейтральні лінії і дотичні до перерізу бруса.
Рівняння нейтральної лінії має вигляд:
![]() , (7.2)
, (7.2)
де z0, y0 – координати точки нейтральної лінії. Позначення інших величин ті ж, що і в формулі (7.1).
З виразу (7.2) видно, що нейтральна лінія не проходить через центр ваги перерізу. При побудові нейтральної лінії визначають відрізки az і ay, які відсікаються нею на головних центральних осях перерізу (див.рис.7.1):
![]() ;
;
![]() .
.
Якщо нейтральна лінія перетинає переріз, то вона ділить його на стиснуту і розтягнуту частини. Тоді для матеріалу, який по-різному опирається розтягу і стиску, є дві ймовірно небезпечні точки: в одній з них діє найбільше розтягуюче напруження, а в другій – найбільше стискаюче. Умова міцності виконується, якщо найбільше розтягуюче напруження не перевищує допустимого напруження при розтягу
pmaxp,
а найбільше по абсолютні величині стискаюче напруження не перевищує допустимого напруження при стиску
сmaxс.
Приклад
Для заданого перерізу визначити допустиме навантаження, якщо відомі координати точки прикладення рівнодіючої всіх навантажень F і величина допустимих напружень: []ст=120МН/м2 і []р=30МН/м2, а також побудувати просторову епюру розподілу напружень по перерізу. Координати точки прикладення рівнодіючої F в системі головних центральних осей yF=8см, zF=-5см.
Розбиваємо складний переріз на ряд простих, центр ваги яких легко визначити. В даному випадку на півкруг, прямокутник і трикутник (рис.7.2).
Для даного перерізу стержня визначаємо положення центра ваги перерізу відносно довільно вибраних допоміжних осей Z0 і Y0 по формулі:
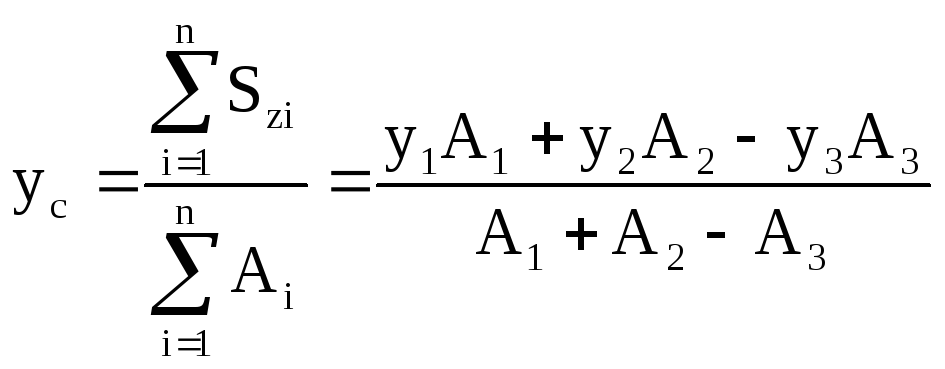 ,
,
де y1=12.55см, y2=5см, y3=1см – відстані від центра ваги півкруга, прямокутника і трикутника до осі Z;
![]() ,
А2=1210=120см2,
,
А2=1210=120см2,
![]() – площі відповідно півкруга, прямокутника
і трикутника.
– площі відповідно півкруга, прямокутника
і трикутника.

Рис.7.2
Отримуємо:
![]() .
.