Файл: Тема 9.doc

Параметры уравнения могут быть определены графическим методом, методом наименьших квадратов и т.д.

Методом наименьших квадратов (см. раздел 9.3) минимизируем выражение:

;

;;; …;.

Например, по параметру :

.

Сделав соответствующие преобразования по всем значениям параметров получим:

,

отсюда:

.

В результате таких преобразований система нормальных уравнений с неизвестными (по числу параметров) имеет вид

(9.8)

Таким образом, обобщенная блок-схема построения множественного уравнения регрессии может быть представлена в следующем виде (рис. 9.6).

Рис. 9.6.Схема построения множественного уравнения регрессии

Одним из способов построения множественных уравнений регрессии является построение модели связи в стандартизованном масштабе.

Оценка влияния каждого факторного признака, включенного в уравнение регрессии, на результативный признак может быть значительно затруднена, если факторные признаки различны по своей сущности и имеют различные единицы измерения. В этих случаях для более точной оценки влияния факторных признаков на результативный используют множественные модели регрессии в стандартизованном масштабе. Модель регрессии в стандартизованном масштабе предполагает, что все значения исследуемых признаков переводятся в стандарты по формуле

---

,

(9.9)

где - значение признака в натуральном масштабе.

Уравнение множественной регрессии в стандартизованном масштабе следующее:

,

(9.10)

где - стандартизованные значения признаков;

- среднее значение стандартизованной переменной соответствующего результативного признака, полученного по уравнению регрессии;

- стандартизованные коэффициенты регрессии.

Параметры многофакторной модели регрессии в стандартизованном масштабе определяются методом наименьших квадратов, рассмотренным выше.

Представим систему нормальных уравнений:

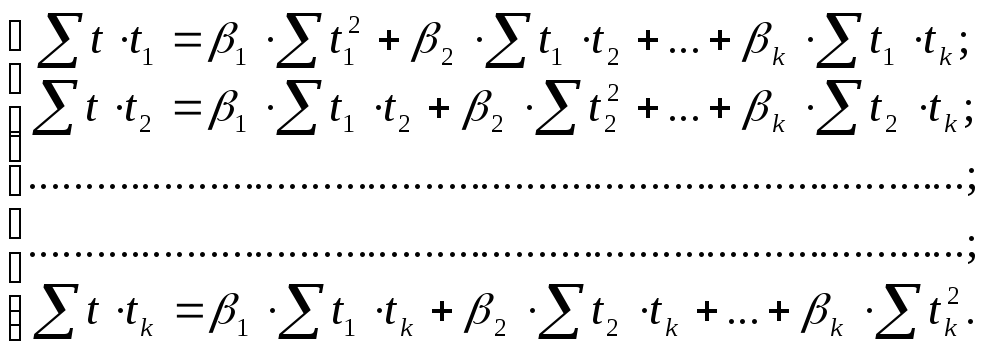
где - значение результативного признака в стандартизованном масштабе.

Коэффициенты дают возможность провести сравнительную оценку силы влияния изменения каждого факторного признака на изменение результативного (моделируемого) признака.

От уравнения в стандартизованном масштабе можно легко перейти к уравнению в натуральном масштабе. Коэффициенты получают из соотношения

,

(9.11)

а свободный член - из выражения

.

---

---

9.5 Оценка существенности связи. Принятие решений на основе уравнения регрессии

Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии.

Значимость коэффициентов регрессии осуществляется с помощью -критерия Стьюдента:

,

(9.12)

где - дисперсия коэффициента регрессии.

Параметр модели признается статистически значимым, если

,

где	уровень значимости критерия проверки гипотезы о равенстве нулю параметров, измеряющих связь, т.е. статистическая существенность связи утверждается при отклонении нулевой гипотезы об отсутствии связи;
	число степеней свободы, которое характеризует число свободно варьирующих элементов совокупности.

Наиболее сложным в этом выражении является определение дисперсии, которая может быть рассчитана двояким способом.

Наиболее простой способ, выработанный методикой экспериментирования, заключается в том, что величина дисперсии коэффициента регрессии может быть приближенно определена по выражению

,

(9.13)

где		дисперсия результативного признака;
		число факторных признаков в уравнении.

---

Более точную оценку величины дисперсии можно получить по формуле:

,

(9.14)

где

величина множественного коэффициента корреляции по фактору с остальными факторами.

Проверка адекватности всей модели осуществляется с помощью расчета -критерия и величины средней ошибки аппроксимации.

Если приили, то- гипотеза о несоответствии заложенных в уравнении регрессии связей реально существующим отвергается. Величинаопределяется по специальным таблицам на основании величиныилии числа степеней свободы:

,,

где		число наблюдений;
		число факторных признаков в уравнении.

Значение средней ошибки аппроксимации не должно превышать 12-15%.

,

---
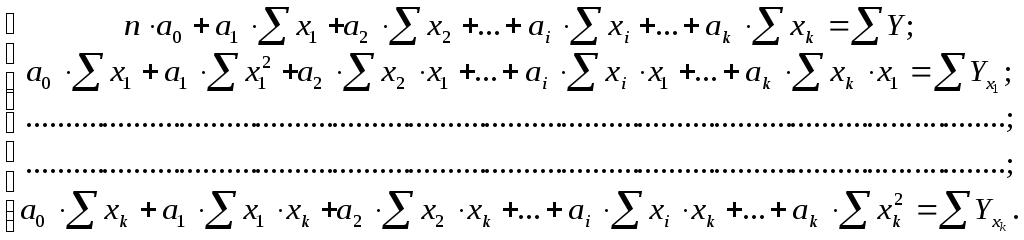
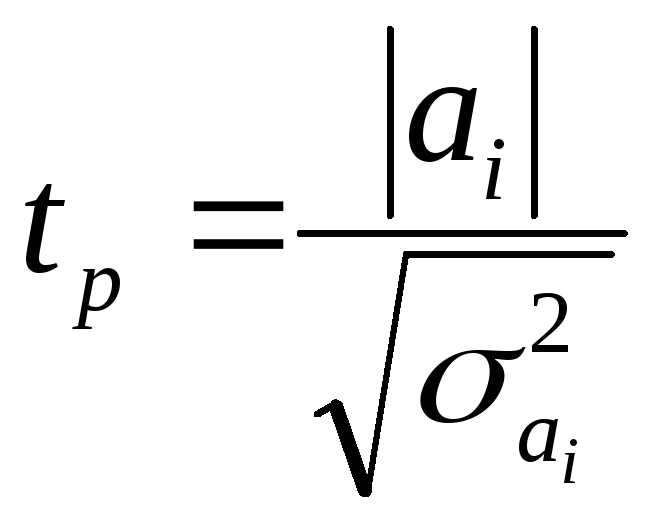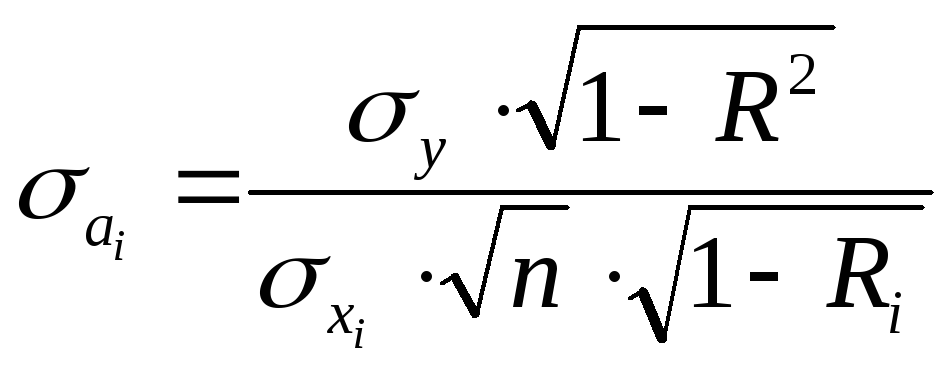