ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.08.2024
Просмотров: 161
Скачиваний: 0
СОДЕРЖАНИЕ
Тема 9 статистическое изучение взаимосвязи социально-экономических явлений
Причинность, регрессия, корреляция
9.2 Основные задачи и предпосылки применения корреляционно-регрессионного анализа
9.3 Парная регрессия на основе метода наименьших квадратов и метода группировок
9.4 Множественная (многофакторная) регрессия
9.5 Оценка существенности связи. Принятие решений на основе уравнения регрессии
9.7 Методы изучения связи социальных явлений
9.8 Непараметрические показатели связи. Ранговые коэффициенты связи
Если же
![]() ,
то это означает, что все точки (
,
то это означает, что все точки (![]() ,
,![]() )
находятся на прямой и зависимость между
)
находятся на прямой и зависимость между![]() и
и
![]() является функциональной. Прямые
регрессии в этом случае совпадают.
Указанное положение распространяется
также на случай нормального распределения
трех и более величин.
является функциональной. Прямые
регрессии в этом случае совпадают.
Указанное положение распространяется
также на случай нормального распределения
трех и более величин.
Линейный коэффициент корреляции
изменяется в пределах от - 1 до 1:
![]() .
Знаки коэффициентов регрессии и
корреляции совпадают. При этом
интерпретацию выходных значений
коэффициента корреляции можно представить
в табл. 9.3.
.
Знаки коэффициентов регрессии и
корреляции совпадают. При этом
интерпретацию выходных значений
коэффициента корреляции можно представить
в табл. 9.3.
Значимость линейного коэффициента
корреляции проверяется на основе
![]() -критерия
Стьюдента. При этом выдвигается и
проверяется гипотеза (
-критерия
Стьюдента. При этом выдвигается и
проверяется гипотеза (![]() )
о равенстве коэффициента корреляции
нулю
)
о равенстве коэффициента корреляции
нулю![]() .
При проверке этой гипотезы используется
.
При проверке этой гипотезы используется![]() -статистика:
-статистика:
|
|
(9.25) |
|||||
|
|
Таблица 9.3 |
|
||||
|
|
Оценка линейного коэффициента корреляции |
|
||||
|
|
Значение линейного коэффициента связи |
Характер связи |
Интерпретация связи |
|
||
|
|
|
Отсутствует |
- |
|
||
|
|
|
Прямая |
С
увеличением
|
|
||
|
|
|
Обратная |
С
увеличением
|
|
||
|
|
|
Функциональная |
Каждому значению факторного признака строго соответствует одно значение результативного признака |
|
||
При выполнении
![]()
![]() -статистика
имеет распределение Стьюдента с входными
параметрами:
-статистика
имеет распределение Стьюдента с входными
параметрами:![]() .
.
Если расчетное значение
![]() (табличное), то гипотеза
(табличное), то гипотеза![]() отвергается, что свидетельствует о
значимости линейного коэффициента
корреляции, а следовательно, и о
статистической существенности зависимости
между
отвергается, что свидетельствует о
значимости линейного коэффициента
корреляции, а следовательно, и о
статистической существенности зависимости
между![]() и
и![]() .
.
Данный критерий оценки значимости
применяется для совокупностей
![]() .
.
При большом числе наблюдений (![]() )
используется следующая формула
)
используется следующая формула![]() -статистики:
-статистики:
|
|
(9.26) |
Для статистически значимого линейного
коэффициента корреляции можно построить
интервальные оценки с помощью
![]() -распределения
Фишера:
-распределения
Фишера:
![]() .
.
Первоначально определяется интервальная
оценка для
![]() по
выражению
по
выражению
|
|
(9.27) |
|
где |
|
|
|
|
|
|
В случае наличия линейной и нелинейной зависимости между двумя признаками для измерения тесноты связи применяют так называемое корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение.
Эмпирическое корреляционное отношение
рассчитывается по данным группировки,
когда![]() характеризует отклонения групповых
средних результативного показателя от
общей средней:
характеризует отклонения групповых
средних результативного показателя от
общей средней:
|
|
(9.28) |
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все эти дисперсии являются дисперсиями результативного признака.
Теоретическое корреляционное отношение определяется по формуле:
|
|
(9.29) |
|
где |
|
|
|
|
|
|
![]()
![]()
Тогда
|
|
(9.30) |
объясняется влиянием факторного признака.
В основе расчета корреляционного отношения лежит правило сложения дисперсий, т.е.
|
|
(9.31) |
|
|
|
|
![]()
Отсюда формула корреляционного отношения принимает вид
|
|
(9.32) |
Корреляционное отношение изменяется
в пределах от 0 до 1 (![]() ),
и анализ степени тесноты связи полностью
соответствует линейному коэффициенту
корреляции (см. табл. 9.3).
),
и анализ степени тесноты связи полностью
соответствует линейному коэффициенту
корреляции (см. табл. 9.3).
Теоретическое корреляционное отношение также может вычисляться по формуле
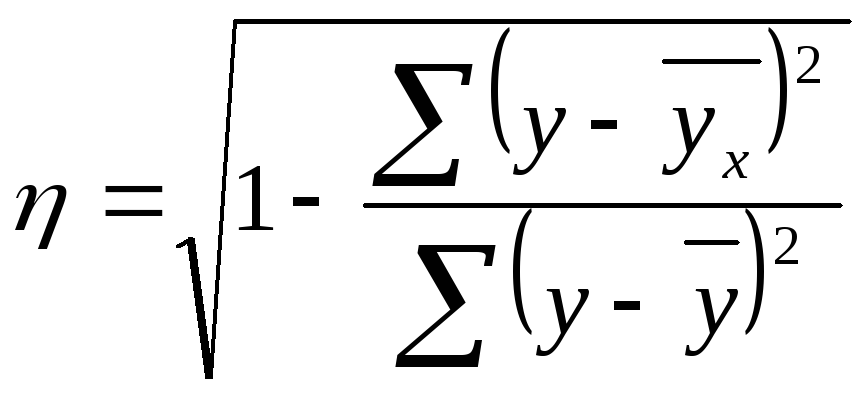 .
.
Корреляционное отношение является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.
Для измерения тесноты связи при множественной корреляционной зависимости, т.е. при исследовании трех и более признаков одновременно, вычисляются множественный, или совокупный, и частные коэффициенты корреляции.
Множественный коэффициент корреляции рассчитывается при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков.
Он вычисляется по формуле
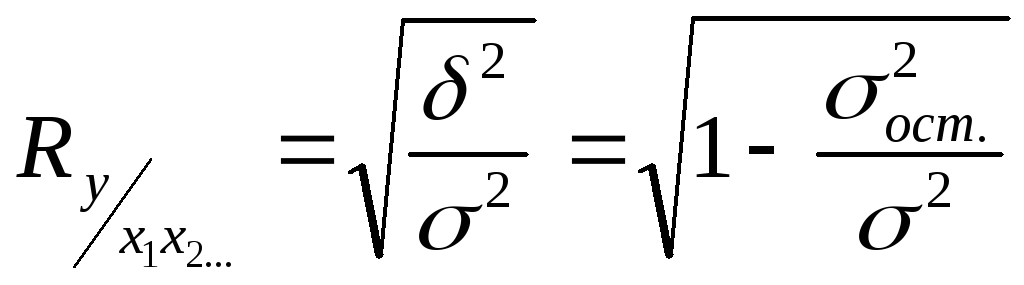
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В случае оценки связи между результативным
(![]() )
и двумя факторными признаками (
)
и двумя факторными признаками (![]() )
и (
)
и (![]() )
множественный коэффициент корреляции
можно определить по формуле
)
множественный коэффициент корреляции
можно определить по формуле
|
|
(9.33) |
|
где |
|
|
Множественный коэффициент корреляции
можно рассчитать, используя парные
коэффициенты
![]() и коэффициенты регрессии в
стандартизованном масштабе (
и коэффициенты регрессии в
стандартизованном масштабе (![]() ):
):
![]()
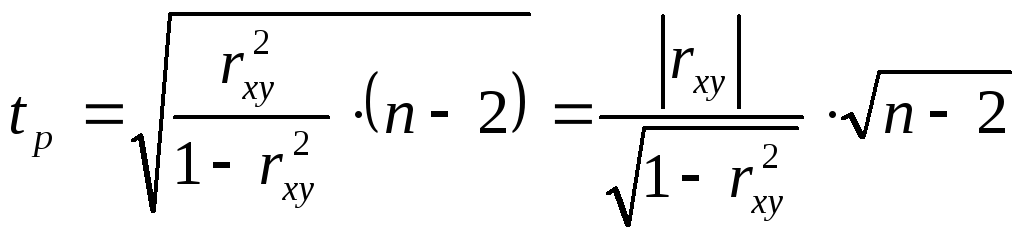 .
.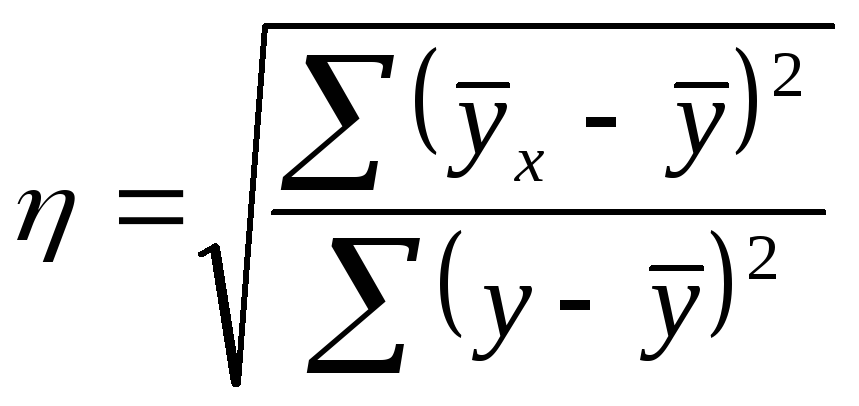 ,
,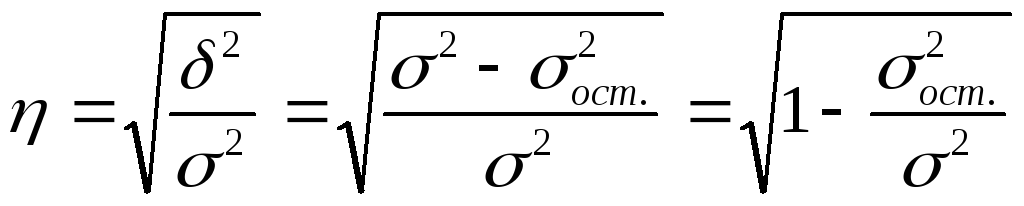 .
.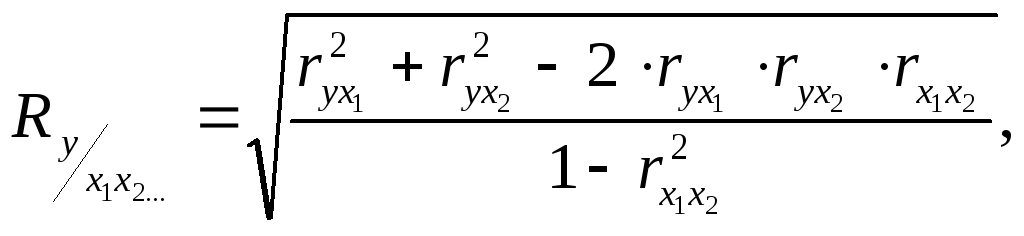 .
.