Файл: деп_тукс_10_11.doc

Английский фантаст Олаф Степлдон еще в тридцатые годы так описывал эту возможность: «В некоем непостижимо сложном космосе всякий раз, когда какое-либо существо встречается с различными альтернативами, оно выбирает не одну, а все... И поскольку в этом мире множество существ и каждое из них постоянно сталкивается со многими альтернативами, то комбинации этих процессов неисчислимы». В пятидесятые годы «размножение вселенных» анализировал уже американский физик Хьюдж Эверетт.

Во всех упомянутых нами гипотезах особая роль неизменно отводится человеку, ибо именно он глядит на окружающий его мир, то есть «измеряет его состояние». «Мы до сих пор не можем постичь, какое место занимает человек в нашей Вселенной, - сказал в одном из интервью Антон Цайлингер. - Возможно, ему отведена куда более важная роль, нежели могли предполагать создатели классической физики».

7. Квантовые вычисления. Квантовые компьютеры.

7.1. Вводные замечания

Ричард Фейнман заметил, что определённые квантово - механические процессы нельзя эффективно моделировать на классическом компьютере. Это замечание привело к более общему утверждению, что для проведения вычислений квантовые процессы являются более эффективными, чем классические. Данное предположение было подтверждено Питером Шором, который разработал квантовый алгоритм разложения целых чисел на простые множители за полиномиальное время.

В квантовых системах пространство вычислений экспоненциально возрастает с размером системы, что и делает возможным экспоненциальный параллелизм. Данный параллелизм может привести к квантовым алгоритмам, которые экспоненциально быстрее классических.

Только к середине 1990-х годов теория квантовых компьютеров и квантовых вычислений утвердилась в качестве новой области науки. По-видимому, первым обратил внимание на возможность разработки квантовой логики венгерский математик И. фон Нейман. Однако в то время еще не были созданы не то что квантовые, но и обычные, классические, компьютеры. А с появлением последних основные усилия ученых оказались направлены в первую очередь на поиск и разработку для них новых элементов (транзисторов, а затем и интегральных схем), а не на создание принципиально других вычислительных устройств.

В 1960-е годы американский физик Р. Ландауэр пытался обратить внимание на то, что вычисления - это всегда некоторый физический процесс, а значит, невозможно понять пределы наших вычислительных возможностей, не уточнив, какой физической реализации они соответствуют. К сожалению, в то время среди ученых господствовал взгляд на вычисление как на некую абстрактную логическую процедуру, изучать которую следует математикам, а не физикам.

По мере распространения компьютеров ученые, занимавшиеся квантовыми объектами, пришли к выводу о практической невозможности напрямую рассчитать состояние эволюционирующей системы, состоящей всего лишь из нескольких десятков взаимодействующих частиц, например молекулы метана СН₄. Объясняется это тем, что для полного описания сложной системы необходимо держать в памяти компьютера экспоненциально большое (по числу частиц) количество переменных, так называемых квантовых амплитуд. Возникла парадоксальная ситуация: зная уравнение эволюции, зная с достаточной точностью все потенциалы взаимодействия частиц друг с другом и начальное состояние системы, практически невозможно вычислить ее будущее, даже если система состоит лишь из 30 электронов в потенциальной яме, а в распоряжении имеется суперкомпьютер с оперативной памятью, число битов которой равно числу атомов в видимой области Вселенной. В то же время, для исследования динамики такой системы можно просто поставить эксперимент с 30 электронами, поместив их в заданные потенциал и начальное состояние. На это, в частности, обратил внимание русский математик Ю. И. Манин, указавший в 1980 году на необходимость разработки теории квантовых вычислительных устройств. В 1980-е годы эту же проблему изучали американский физик П. Бенев, явно показавший, что квантовая система может производить вычисления, а также английский ученый Д. Дойч, теоретически разработавший универсальный квантовый компьютер, превосходящий классический аналог.

Большое внимание к проблеме разработки квантовых компьютеров привлек Р. Фейнман. Благодаря его авторитетному призыву число специалистов, обративших внимание на квантовые вычисления, увеличилось во много раз.

И все же долгое время оставалось неясным, можно ли использовать гипотетическую вычислительную мощь квантового компьютера для ускорения решения практических задач. В 1994 году американский математик П. Шор предложил квантовый алгоритм, позволяющий проводить быструю факторизацию больших чисел. По сравнению с лучшим из известных на сегодня классических методов квантовый алгоритм Шора дает многократное ускорение вычислений, причем, чем длиннее факторизуемое число, тем значительней выигрыш в скорости. В случае классического алгоритма увеличение факторизуемого числа приводит к экспоненциальному росту требуемых ресурсов. Например, для разложения на множители 500-значного числа нужно в 100 млн. раз больше итераций, чем для 250-значного числа. Для алгоритма Шора объём необходимых ресурсов растёт лишь полиномиально – 500-значное число требует всего в 8 раз больше шагов, чем 250-значное.

Оказывается, используя законы квантовой механики, можно построить такие компьютеры, для которых задача факторизации (и многие другие!) не составит большого труда. Согласно оценкам, квантовый компьютер с памятью объемом всего лишь около 10 тысяч квантовых битов способен разложить 1000-значное число на простые множители в течение всего нескольких часов! Алгоритм быстрой факторизации представляет, например, огромный практический интерес для различных спецслужб, накопивших банки нерасшифрованных сообщений.

В 1997 году Л. Гровер предложил квантовый алгоритм быстрого поиска в неупорядоченной базе данных. (Пример такой базы данных - телефонная книга, в которой фамилии абонентов расположены не по алфавиту, а произвольным образом.) Задача поиска, выбора оптимального элемента среди многочисленных вариантов очень часто встречается в экономических, военных, инженерных задачах, в компьютерных играх. Алгоритм Гровера позволяет не только ускорить процесс поиска, но и увеличить примерно в два раза число параметров, учитываемых при выборе оптимума.

Реальному созданию квантовых компьютеров препятствует серьезная проблема - ошибки, или помехи. Дело в том, что один и тот же уровень помех гораздо интенсивнее портит процесс квантовых вычислений, чем классических. Пути решения этой проблемы наметил в 1995 году П. Шор, разработав схему кодирования квантовых состояний и коррекции в них ошибок.

Время, которое необходимо для осуществления определённых вычислений, можно уменьшить, используя параллельные процессоры. Чтобы достичь экспоненциального уменьшения времени, требуется экспоненциально увеличить число процессоров, а, следовательно, и объём физического пространства. В квантовой системе для экспоненциального уменьшения времени, требуется лишь линейное увеличение объёма необходимого физического пространства. Это явление связано непосредственно с квантовым параллелизмом (Дойч и Джоша, 1992).

Существует ещё одна важная особенность. Пока квантовая система выполняет вычисления, доступ к результатам ограничен. Процесс доступа к результатам — это процесс измерения, который возмущает квантовое состояние, искажая его. Может показаться, что здесь ситуация ещё хуже, чем с классическими вычислениями. Получается, что мы можем только считать результат выполнения одного из параллельных процессов, а поскольку измерение является вероятностным, то мы даже не можем выбирать, результат какого процесса мы получим.

Но за прошедшие несколько лет люди обнаружили нестандартные пути искусного решения задачи измерения, чтобы использовать преимущества квантового параллелизма. Манипуляции подобного рода не имеют аналогов в классической теории и требуют применения нетрадиционных приемов программирования. Один из таких приёмов заключается в управлении квантовым состоянием таким образом, чтобы могло быть считано общее свойство всех результирующих значений, такое как симметричность или период функции. Подобная техника используется в алгоритме разложения на множители Шора. При другом подходе квантовые состояния преобразуются так, чтобы увеличить вероятность считывания интересующего нас результата вычислений. Этот приём используется в поисковом алгоритме Гровера

7.2. Квантовый регистр

Квантовый регистр (ячейка памяти) устроен почти так же, как и классический. Это цепочка квантовых битов, над которыми можно проводить одно- и двухбитовые логические операции.

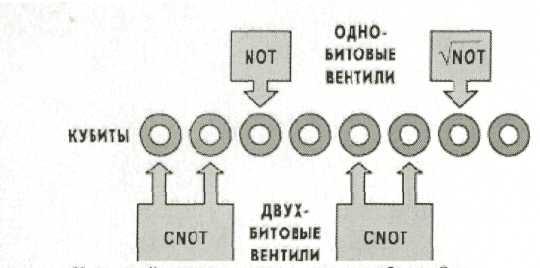
Рис. 7.1. Квантовый регистр – цепочка квантовых битов. Одно- или двухбитовые квантовые вентили осуществляют логические операции (NOT, CNOT) над кубитами или парами кубитов

Операция CNOT – контролируемое НЕ, Controlled NOT, аналог исключающего ИЛИ в классических компьютерах – это двухкубитная операция. Однокубитные операции – опрации НЕ и преобразование Адамара. Умея выполнять эти операции над кубитами, можно реализовать любую программу для квантового компьютера. К базовым состояниям квантового регистра, образованного L кубитами, относятся, так же как и в классическом, все возможные последовательности нулей и единиц длиной L. Всего может быть 2^L различных комбинаций. Их можно считать записью чисел в двоичной форме от 0 до 2^L-1 и обозначать 0,1,2,3, 2^L-1. Однако эти базовые состояния не исчерпывают всех возможных значений квантового регистра (в отличие от классического), поскольку существуют еще и состояния суперпозиции, задаваемые комплексными амплитудами, связанными условием нормировки. Классического аналога у большинства возможных значений квантового регистра (за исключением базовых) просто не существует. Состояния классического регистра существенно уступают всей совокупности состояний квантового компьютера.

Пусть на регистр осуществляется внешнее воздействие, например, поданы электрические импульсы или направлены лазерные лучи. Если это классический регистр, то импульс, который можно рассматривать как вычислительную операцию, изменит L переменных. Если же это квантовый регистр, то тот же импульс может одновременно преобразовать до 2^L переменных. Таким образом, квантовый регистр, в принципе, способен обрабатывать информацию в 2^L / L раз быстрее по сравнению со своим классическим аналогом. Отсюда сразу видно, что маленькие квантовые регистры (L<20) могут служить лишь для демонстрации отдельных узлов и принципов работы квантового компьютера, но не принесут большой практической пользы, так как не сумеют обогнать современные ЭВМ, а стоить будут заведомо дороже. В действительности квантовое ускорение обычно значительно меньше, чем приведенная грубая оценка сверху (это связано со сложностью получения большого количества амплитуд и считывания результата), поэтому практически полезный квантовый компьютер должен содержать тысячи кубитов. Но, с другой стороны, понятно, что для достижения действительного ускорения вычислений нет необходимости собирать миллионы квантовых битов. Компьютер с памятью, измеряемой всего лишь в килокубитах, будет в некоторых задачах несоизмеримо быстрее, чем классический суперкомпьютер с терабайтами памяти.