Файл: деп_тукс_10_11.doc

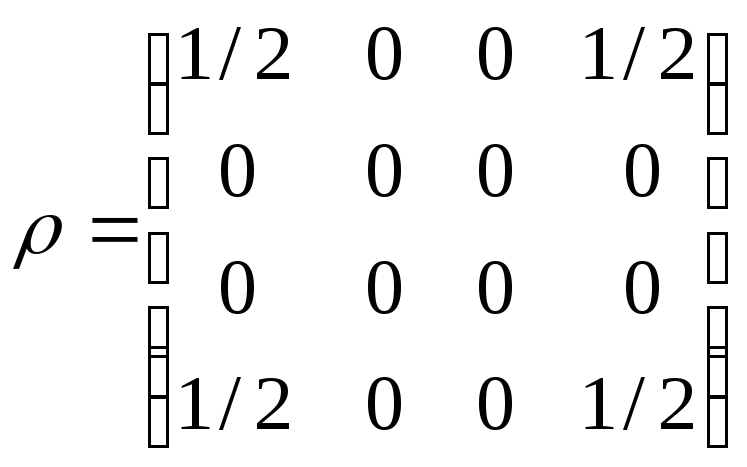. (2.6)

Система с равной вероятностью 1/2 находится в состояниях |00ñ и |11ñ — это диагональные элементы. Корреляции между этими состояниями максимальны (недиагональные элементы). Недиагональные элементы равны друг другу и расположены симметрично, как и должно быть для любой матрицы плотности.

При измерении этого нелокального состояния (при декогеренции) мы получим одно из двух локальных (сепарабельных) состояний |00ñ или |11ñ с равной вероятностью.

Существует простой способ проверить, относится ли какая-либо матрица плотности к чистому состоянию или нет. Если умножить матрицу саму на себя, и она при этом не изменится (получится та же самая матрица), то есть если выполняется равенство ρ² = ρ, то можно сразу сказать, что данная матрица плотности описывает чистое состояние, и для него может быть записан вектор состояния. Такие матрицы, которые не меняются при умножении самой на себя, называются идемпотентными. Таким образом, любая матрица плотности чистого состояния — идемпотентная.

Если система незамкнутая (открытая), то это смешанное состояние, и тогда она не описывается вектором состояния, но ее по-прежнему можно описать матрицей плотности. Например, максимально смешанное состояние:

. (2.7)

Его уже нельзя записать в виде вектора состояния. В этом случае нет корреляций между состояниями |00ñ |01ñ |10ñ |11ñ, и при измерении можно получить любое из этих состояний с равной вероятностью 1/4.

Матрица плотности такого вида получается, если необходимо описать состояние одной из подсистем, например А, в случае максимально запутанного состояния типа (2.5). Так, если рассмотреть частичный след по подсистеме B и получить частичную матрицу плотности размерностью 2 × 2, которая описывает подсистему А, то эта матрица плотности будет соответствовать максимально смешанному состоянию и иметь вид:

. (2.8)

Подсистема А с равной вероятностью 1/2 может находиться в состоянии |0ñ или |1ñ.

Необходимо отметить - когда мы говорим «состояние системы», то смысл этого выражения обычно зависит от контекста. Речь может идти о состоянии, полученном в результате измерения (декогеренции), то есть об одном из реализованных собственных состояний системы (об одном из диагональных состояний матрицы плотности). Или имеется в виду исходное состояние, то есть сам вектор состояния (вся матрица плотности), тогда по ее структуре можно судить о квантовой запутанности и о корреляциях. В простых случаях, например, для матрицы плотности типа (2.6) (когда 1/2 стоят по четырем углам, а остальные нули), сразу можно сказать, что это максимально запутанное состояние.

2. 2. О квантовой информации

Квантовая информация - новая область науки и технологии, сочетающая в себе разделы физики, математики, кибернетики и инженерии. Ее целью является выяснение роли фундаментальных законов физики, открытых в XX-ом веке, в процессах получения, передачи и обработки информации. Теория классической информации не может адекватно ответить на вопрос, как информация может быть использована в квантовом мире. Некоторые выводы теории квантовой информации могут быть представлены как обобщение классической теории в тех случаях, когда информация передается и хранится с помощью квантовых состояний, а не в терминах классических битов.

Квантовая теория информации устанавливает связь между мерой квантовой запутанности и информацией. Возможно, на фундаментальном уровне нет ничего, кроме квантовой информации, которая в процессе декогеренции проявляется в пространствах меньшей размерности в виде локальных объектов.

Целью квантовой теории информации является выявление общих принципов реализации квантовых вычислений и квантового компьютера. Важной задачей является отыскание новых способов обработки информации и исследование свойств сцепленных квантовых состояний.

Вычисление - это процесс, в ходе которого происходит определенное для каждой логической операции (ЛО) нелинейное взаимодействие потоков информации друг с другом и их преобразование. В зависимости от типа ЛО определенным образом изменяется состояние логического элемента (ЛЭ), а поступающая на его входы информация либо передается далее, либо как-то преобразуется. Управление или преобразование происходит под воздействием внешних сигналов. Это, например, переключение или инверсия (01, 10), запись, сброс. Носитель информации на физическом уровне называется сигналом.

Общеизвестно, что объекты микромира ведут себя совершенно необычно с точки зрения классического мира. Так, наблюдение за атомом возмущает его движение, в то же время в отсутствие наблюдения, атом как бы размыт по пространству и скоростям (отсутствие траектории, соотношение неопределенности Гейзенберга), как будто бы он находился в нескольких различных местах в одинаковые моменты времени.

Таким образом, до сих пор квантовые эффекты, связанные с малостью размеров различных устройств воспринимались как преграда на пути к миниатюризации электронных устройств. Квантовая информатика должна выяснить, как использовать фундаментальные квантовые свойства.

Один из основных вопросов теории информации заключается в том, какое количество информационного ресурса необходимо для выполнения данной задачи? Например, сколько шагов надо сделать для решения задачи факторизации, т.е. разложения простых сомножителей числа? Для простых сомножителей данного 300–значного числа классический алгоритм требует примерно 51024 шагов или около 150 тыс. лет при скорости вычислений порядка терагерц, а квантовый алгоритм требует 51010 шагов и выполняется меньше секунды при той же скорости.

Б. Шумахер выделяет такие элементы информатики:

1. Выбрать физические ресурсы, например, строку битов, действительно рассматриваемых не абстрактно, а как физическую систему.

2. Сформулировать задачу обработки информации, выполняемую с помощью физического ресурса.

3. Выбрать критерий успешного выполнения задачи.

Итак, главный вопрос теории информации таков: какова минимальная величина физического ресурса для выполнения задачи обработки информации в соответствии с критерием успеха?

В квантовой теории информации эти процедуры приобретают специфические черты: в качестве физического ресурса здесь выступают сцепленные состояния, при обработке информации необходимо управлять ими, а критерий успеха менее определён и очевиден, чем в классическом случае.

Одним из приложений квантовой информатики является криптография. Здесь уже разработаны и реализованы алгоритмы, использующие такие свойства квантовых объектов, как неклонируемость и невозможность измерения (перехвата сообщения) без возмущения. Основной выигрыш в квантовых криптографических протоколах - даже не абсолютная их секретность, а то, что сам факт подслушивания становится известным для пользователей, т.к. любое вторжение в квантовую систему с неизбежностью изменит её состояние, что сразу станет известно субъектам, обменивающихся информацией.

Итак, Проблема 1 -уменьшение размеров интегральных схем, т.е. отдельных элементов. Естественный предел здесь - характерный масштаб атома, когда вступают в силу законы микромира, т.е. квантовой механики. Проблема 2- уменьшение доли рассеиваемой энергии. Логически обратимые операции - те, которые не сопровождаются рассеянием энергии (Ландауер, 1961г.). Универсальный цифровой компьютер типа вычислительной машины Тьюринга может быть построен на логически и термодинамически обратимых ЛЭ так, что энергия будет рассеиваться только за счет необратимых периферийных процессов (типа ввода информации в машину либо ее вывода).

Для выполнения классических вычислений необходима физическая система, имеющая два устойчивых состояния, например, триггеры - в радиоэлектронике.

Квантовый же компьютер - физическое устройство, выполняющее логические операции над квантовыми состояниями путем унитарных преобразований, не нарушающих квантовые суперпозиции в процессе вычислений. Схематично, работа квантового компьютера может быть представлена как последовательность трех операций:

1. “ЗАПИСЬ” (приготовление начального состояния),

2. “ВЫЧИСЛЕНИЕ” (унитарные преобразования начальных состояний)

3. “ВЫВОД” результата (измерение, проецирование конечного состояния).

Также сюда следует отнести вспомогательную операцию “СБРОС”, приводящую регистр к основному состоянию.

Рассмотрим связь информации и энтропии. Пусть имеется лента, разбитая на ячейки - классический регистр. Если в каждой ячейке может быть помещен только один из двух символов, то говорят, что в ячейке содержится бит информации. Очевидно, что в регистре, содержащем N ячеек содержится N бит информации и в нем можно записать 2^N сообщений. Итак, информационная энтропия измеряется в битах:

(2.9)

Здесь Q_N = 2^N - полное число различных сообщений. Из (2.9) ясно, что информационная энтропия равна минимальному числу двоичных ячеек, с помощью которых можно записать некую информацию.

Определение (2.9) можно переписать по-другому. Пусть у нас имеется множество Q_N различных сообщений. Найдем вероятность того, что необходимое нам сообщение совпадет со случайно выбранным из общего числа Q_N различных сообщений. Она равна, очевидно, P_N = 1/Q_N. Тогда определение (2.9) запишется как:

(2.10)

Чем больше число ячеек N, тем меньше вероятность P_N и тем больше информационная энтропия H_B, содержащейся в данном конкретном сообщении.

Например, число букв алфавита равно 32 (без буквы ё), т.е. 2⁵. Чтобы каждой букве сопоставить определенную комбинацию двоичных чисел необходимо иметь 5 ячеек. Добавив к строчным буквам заглавные, мы удваиваем число символов, которые хотим закодировать - их станет 64 = 2⁶ - т.е. добавляется лишний бит информации H_B = 6. Здесь H_B - объем информации, приходящийся на одну букву (строчную или заглавную). Однако такой прямой подсчет информационной энтропии не совсем точен, поскольку в алфавите есть буквы, которые встречаются реже или чаще. Тем буквам, которые встречаются реже, можно отдать б'ольшее количество ячеек, а на часто встречающихся буквах - сэкономить и отдать им те состояния регистра, которые занимают меньшее количество ячеек. Точное определение информационной энтропии было дано Шенноном: