Файл: деп_тукс_10_11.doc

5. Квантовая криптография

5.1. Понятие о криптографии

Желание людей переписываться с сохранением секретов является, по меньшей мере, настолько же древним, как и сама письменность. Криптология («криптос» - спрятанный, «логос» - слово) - это наука о защите сообщения. Она включает в себя криптографию – искусство создания кодов и криптоанализ – искусство взламывания кодов. Криптография – это искусство скрытия информации в последовательности битов от любого несанкционированного доступа. Для достижения этой цели используют шифрование: сообщение с помощью некоторого алгоритма комбинируется с дополнительной секретной информацией (ключом), в результате получается криптограмма.

Известно, что спартанцы около 400 г. до н.э. уже применяли криптографию. Устройство, называемое «скитал», состояло из конусообразной дубинки, вокруг которой по спирали наматывалась полоска из пергамента или кожи, несущая сообщение. Сообщение писалось вдоль дубинки, по одной букве на каждом витке полоски. Получатель сообщения наматывал пергамент на другую дубинку такой же формы и мог прочитать сообщение.

Юлий Цезарь использовал простой метод подстановки букв: каждая буква заменялась на другую, следующую по алфавиту через три. Этот метод называют шифром Цезаря независимо от размера смещения.

Эти простые примеры уже содержат два базовых метода шифрования – перестановку и подстановку.

Долгое время способы разработки алгоритмов шифрования определялись исключительно хитростью и изобретательностью их авторов. Лишь в 20 веке этой областью стали заниматься математики и физики.

Современная же криптология родилась одновременно с вычислительной техникой. По выражению Р.Л. Ривеста (одного из изобретателей популярной системы кодирования RSA) криптоанализ был «повивальной бабкой вычислительной техники».

5.2. Ключи и их распределение

Для любой системы передачи информации характерны следующие условные действующие лица: объекты «Алиса» и «Боб», обменивающиеся информацией, и некто «Ева», пытающаяся перехватить информацию. Задача заключается в том, чтобы исключить возможность расшифровки информации Евой или хотя бы сделать расшифровку достаточно трудной для Евы.

Изначально защита криптотекста зависела от секретности обеих процедур шифрования и дешифровки. В настоящее время используются шифры, в которых можно открыть алгоритм шифрования и расшифровки кому угодно, без угрозы для сохранения секретности конкретной криптограммы. В таких шифрах набор специальных параметров, называемых ключом, подаётся вместе с открытым текстом, на вход в алгоритме зашифровки и, вместе с криптограммой, на вход алгоритма расшифровки. Это можно записать в виде:

, и, наоборот, ,

где P - открытый текст, С – криптотекст (криптограмма), k – криптографический фический ключ, E и D – операции шифровки и расшифровки, соответственно.

Классический подход состоит в том, что ключ, использующийся как для шифровки, так и для расшифровки сообщения, должен быть известен только Алисе и Бобу. Такие системы называются криптосистемами с закрытым ключом. Надёжность процедуры шифрования доказана только для метода «одноразовых блокнотов», предложенного в 1917 году Гильбертом Вернамом. Идея его состоит в том, что Алиса и Боб обмениваются набором общих секретных ключей, каждый из которых используется для шифрования только одного сообщения. Ключи генерируются случайно и никакой информации не несут.

Рассмотрим простой пример. Выберем простой цифровой алфавит из заглавных букв и некоторых знаков препинания

Тогда для получения криптограммы

добавим к числам открытого текста (верхний ряд цифр) числа из ключа (средний ряд чисел), которые выбраны случайно из области от 0 до 29, и возьмём остаток от деления суммы на 30. Например, первая буква сообщения «S» записывается в открытом тексте как «18», затем суммируем 18+15=33 и 33=130+3, следовательно, в криптограмме 03. Шифрование и расшифровку можно записать, соответственно, как P+k(mod 30)=C и C-k(mod 30)=P.

Позже Клод Шеннон показал, что, если ключ действительно случайный, если он такой же длины, что и само сообщение, и если он никогда не используется повторно, то одноразовая передача сообщения защищена абсолютно.

Существует, однако, проблема распределения ключа. Как только ключ установлен, последующее сообщение предполагает пересылку по некоему каналу, в том числе, возможно, по каналу, подверженному пассивному прослушиванию. Этот этап действительно защищён. Однако, чтобы определить ключ два пользователя, у которых исходно нет никакой общей секретной информации, должны на какой-то стадии своего общения использовать некий очень надёжный и секретный канал. Поскольку перехват есть серия измерений, проводимых подслушивающим агентом, то любое классическое распределение можно в принципе подслушать, причём пользователи не узнают, что имел место перехват. Это не было бы большой проблемой, если бы ключ был установлен раз и навсегда. В этом случае пользователи могли бы задействовать достаточно ресурсов, например, хранение в сейфе и охрана, чтобы гарантировать, что ключ прибудет к адресату в сохранности. Однако, поскольку ключ необходимо обновлять с каждым новым сообщением, такое распределение ключа стало бы недопустимо дорогим. По этой причине в большинстве приложений не требуют абсолютной секретности, но вместо этого используют менее дорогие и менее защищённые системы. Иначе говоря, конфиденциально обменяться сообщением позволяют ключи, но как обменяться самими ключами с обеспечение секретности?

Если используется постоянный закрытый ключ, то расшифровка сообщения зависит от вычислительной мощности системы и времени. В США, например, используют стандарт DES (Data Encription Standart), принятый в 1977 г. Он используется для важной несекретной информации, например, для коммерческих трансакций. Используется короткий ключ из 64 битов, 56 из которых используются напрямую в алгоритме, а 8 – для детектирования ошибок. Система шифрует блоки из 64 битов открытого текста: длинный открытый текст разрезается на блоки, и затем ключ используется при шифровании каждого из них. Поскольку длина ключа меньше, чем длина кодируемого сообщения, то механизм защиты не является абсолютно надёжным. Если попытаться угадать ключ методом проб и ошибок, нужно перебрать 256 всевозможных значений. И хотя этот объём вычислений очень велик, в настоящее время уже имеются данные о возможности взлома подобных систем. Рекордно короткое время составляет 22 час 15 минут при распределённой обработке информации в компьютерной сети.

Таким образом, можно достичь полной секретности при коммуникации путём одноразовых блокнотов, если решить проблему распределения ключа. Существуют два решения – математическое и физическое.

5.3. Открытые ключи

Теория шифрования с использованием открытого ключа была создана Уэтфилдом Диффи и Мартином Хеллманом в 1976 г. В этой системе Боб имеет общедоступный код для шифрования и закрытый код для расшифровки сообщений. Криптосистемы с открытым ключом основываются на так называемых односторонних функциях: по некоторому х легко вычислит функцию f(x), но, зная f(x), трудно вычислить x.

Первый алгоритм, основанный на теории Диффи-Хеллмана, был предложен Роном Райвестом, Эдди Шамиром и Леонардом Эдлманом в 1977 г. (RSA-алгоритм). Алгоритм RSA встроен в большинство операционных систем, а также во множество приложений, используемых в различных устройствах – от смарткарт до сотовых телефонов. Поэтому на этот продукт фирмы RSA Data Security Inc – программу, реализующую алгоритм шифрования с открытым ключом RSA, продано наибольшее количество лицензий – более 450 миллионов. Алгоритм RSA основан на разложении простого числа на множители. Известно, что вычислить произведение двух простых чисел легко. В то же время, обратная задача-разложение числа на простые множители, достаточно трудоёмка, поскольку время вычислений экспоненциально возрастает при увеличении количества битов в исходном числе. В системах с открытым ключом пользователям не надо договариваться о секретном ключе перед тем, как послать сообщение. Они работают по принципу сейфа с двумя ключами, так что есть один общий открытый ключ, чтобы его запереть, и ещё один секретный ключ, чтобы его отпереть. У всех есть ключ, запирающий сейф, но только у кого-то одного есть ключ, который снова его откроет, так что кто угодно может положить в сейф сообщение, но только один человек может его оттуда забрать. Криптосистему с открытым ключом можно пояснить с помощью механической аналогии, рис. 5.1.

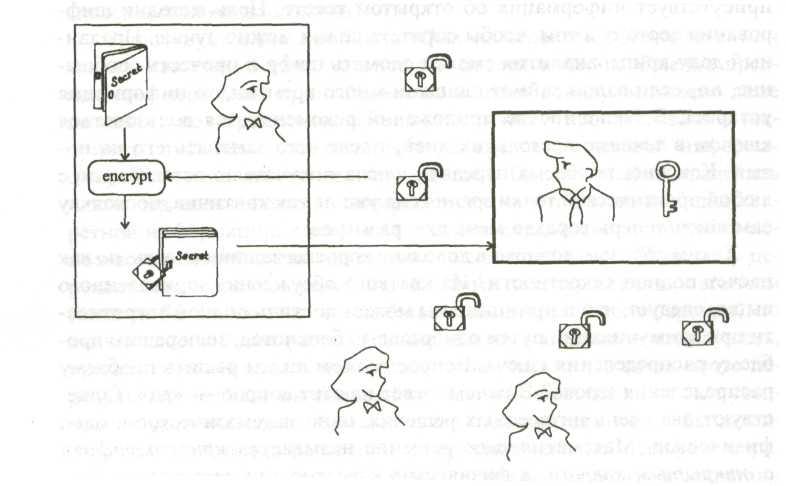
Пусть Алиса и Боб – два лица, которые хотят секретно общаться, а Ева их подслушивает. Пусть Боб может изготовить много висячих замков, и любой желающий послать Бобу секретное сообщение может получить открытый замок, который изготовил Боб. Открытый висячий замок можно рассматривать как открытый ключ. Один из них берёт себе Алиса. Как только Алиса закрыла замок, только Боб может его открыть, потому что только у него есть секретный ключ. Таким образом, Алиса может запереть любые данные по своему усмотрению и послать их Бобу с этим замком. Когда данные заперты, только Боб имеет к ним доступ благодаря наличию у него секретного ключа. Эти системы основаны на том факте, что некоторые математические операции легче провести в одном направлении, чем в другом. Поэтому в таких системах нет проблемы распределения ключей, однако, их надёжность основана на процедуре разложения больших целых чисел на простые множители (факторизации). Например, безопасность RSA, популярной системы с открытым ключом, основана на трудности факторизации больших чисел: чтобы факторизовать число из N десятичных цифр, компьютеру требуется число шагов, растущее экспоненциально с увеличением N, так что с увеличением N задача быстро становится неразрешимой.