ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.08.2024
Просмотров: 361
Скачиваний: 0
СОДЕРЖАНИЕ
Теории управления квантовыми системами.
1. Основные понятия и определения квантовой механики
1.1. Чистые и смешанные состояния
2. Элементы квантовой теории информации
2. 3. Преобразование одного кубита
2.5. Перепутывание и квантовая неразличимость
2.6. Логический элемент «управляемое не»
3. Парадокс эйнштейна – подольского – розена (эпр)
5.4 Понятие о квантовой криптографии
5.4.1. Защита посредством неортогональных состояний
5.4.2. Защита посредством перепутывания
5.4.3. Практическая реализация квантово – криптографических систем
6.2. Протокол квантовой телепортации
6. 3. Обзор некоторых экспериментальных результатов по квантовой телепортации
6.4. Заключительные замечания: возможна ли телепортация макрообъекта?
7. Квантовые вычисления. Квантовые компьютеры.
7.4.2. Моделирование вероятности
7.4.3. Алгоритм разложения на простые множители или алгоритм Шора
7.5. Общие требования к квантовым компьютерам Практическая реализация
В классической физике сила может действовать наряду с другой, и они вполне мирно «уживаются» друг с другом, а при их сложении мы получаем такую же обычную силу, которая не хуже и не лучше других сил. Только если мы сложим две противоположные и одинаковые по модулю силы, их равнодействующая будет равна нулю. Силы тогда взаимно компенсируются, они как бы «уничтожают» друг друга, и на тело вообще никакие силы действовать не будут.
В квантовой теории все состояния несовместимы друг с другом. Но если мы сложим, например, два таких взаимоисключающих состояния, то уже не сможем сказать, что система при этом «уничтожится». Система при квантовом подходе может «исчезнуть» только в одном случае — если у нее нет вообще никаких состояний, а в случае суперпозиции мы имеем как минимум два. Отсутствие системы как элемента реальности в квантовой теории возможно лишь тогда, когда мы вообще не можем сопоставить с системой никаких состояний.
В случае суперпозиции состояний система имеет два различных состояния в качестве потенциально возможных локальных своих проявлений. Это те состояния, которые можно явно наблюдать и зафиксировать, но, чтобы их «проявить», нам необходимо с системой каким-то образом «проконтактировать». Здесь есть два принципиально различных варианта: во-первых, произвести прямое измерение системы, то есть осуществить взаимодействие с измерительным прибором (окружением). В этом случае мы просто разрушаем суперпозицию состояний и «проявляем» одно из потенциальных состояний системы в его локальном, привычном для нас материальном облике. Этот физический процесс называется декогеренцией. Второй вариант: «проявлять» то или иное локальное состояние при помощи так называемых унитарных (обратимых) операций. В этом случае сохраняется возможность снова перевести систему в суперпозиционное состояние. В этом заключается принципиальное отличие от первого варианта, где такая возможность утрачивается. Точнее, реализовать ее можно было только в том случае, если бы мы умели управлять состоянием всей объединенной системы, в состав которой вошла наша исходная система при взаимодействии.
Чистым состоянием (ЧС) называется такое состояние системы, которое может быть описано одним вектором состояния. Система в принципе может быть описана одной волновой функцией (вектором состояния, волновым вектором). И основное различие между чистым и смешанным состоянием в этом и заключается — существует или нет принципиальная возможность полностью описать состояние системы одним вектором состояния. Если это можно сделать — состояние чистое, если нет — смешанное.
Очевидно, что мы можем описать систему одним вектором состояния только в том случае, если она замкнута, изолирована. Под замкнутостью понимается отсутствие любых корреляций системы с окружением, как классических, так и нелокальных квантовых. Замкнутость — необходимое условие для чистого состояния. В противном случае система будет взаимодействовать с окружением и не может быть полностью описана одним лишь вектором состояния — придется учитывать волновые векторы окружения. Замкнутость — это также и достаточное условие для чистого состояния, поскольку вся информация, необходимая для полного описания системы, находится в ней самой, и ее достаточно для принципиальной возможности записать вектор состояния всей системы.
В квантовой механике понятие чистого состояния и понятие замкнутой системы тождественны. Если квантовая система может быть описана одним вектором состояния, говорят, что она находится в чистом состоянии. Для замкнутых систем такая ситуация имеет место по определению.
Остановимся чуть более подробно на замкнутой системе и зададимся вопросом: «В каком состоянии должны находиться подсистемы, и какие корреляции между ними возможны, чтобы состояние всей системы оставалось замкнутым, то есть чистым состоянием?» Здесь возможны два варианта. Самый простой — когда вся система состоит из подсистем, каждая из которых, в свою очередь, сама является замкнутой. В данном случае каждая подсистема находится в чистом состоянии, обладая при этом своим независимым вектором состояния в пространстве с размерностью в гильбертовом пространстве меньшей, чем размерность всей системы. При таком условии вся система может быть разложена по независимым подсистемам. Вектор состояния всей системы и размерность ее гильбертова пространства будет равен тензорному произведению векторов состояния подсистем. В отличие от обычного произведения матриц (строка на столбец), при тензорном умножении каждый элемент первой матрицы умножается на всю вторую матрицу. Это же относится к векторам как частному случаю матриц. Такое состояние системы называется сепарабельным (разделимым).
Это то, на чем стоит вся классическая физика. Если бы не существовало такого варианта чистого состояния, то не было бы и классической физики. Другой вариант чистого состояния — когда система находится в когерентной суперпозиции состояний всех ее подсистем.
В терминах квантовой физики этот случай соответствует ЧС системы, в которой существуют лишь нелокальные квантовые корреляции. Такое состояние в квантовой физике называется чистым запутанным состоянием (ЧЗС).
И самое интересное, что классических корреляций в ЧС нет и быть не может.
Таким образом, ЧС бывают либо сепарабельными, либо ЧЗС. Итак, чистые квантовые состояния бывают либо квантово-коррелированными (запутанными), либо вообще некоррелированными. В случае чистых состояний любые корреляции являются квантовыми, то есть соответствуют запутанным состояниям.
Некоррелированность, то есть отсутствие вообще каких-либо корреляций, как классических, так и квантовых, — это сепарабельные состояния.
Итак, непосредственно из основ квантовой физики следует, что:
● замкнутая система находится в чистом состоянии;
● в замкнутой системе корреляции (и классические, и квантовые) между подсистемами могут отсутствовать вовсе (в случае не взаимодействующих подсистем, то есть сепарабельного состояния);
● в замкнутой системе корреляции между подсистемами могут быть только нелокальными квантовыми (для взаимодействующих подсистем);
● в замкнутой системе отсутствуют классические корреляции между ее подсистемами.
Мы, вместе с окружающими нас объектами, являемся частью Вселенной, при этом классически взаимодействуем с окружением и вовсе не находимся в нелокальном состоянии. Как это сопоставить с тем, что было сказано выше? Никакого противоречия здесь нет, и квантовая механика также отвечает на этот вопрос. Все дело в том, что мы, вместе с окружающими нас объектами, являемся именно частью системы, а классические корреляции отсутствуют во всей системе целиком. То есть в пространстве состояний (гильбертовом пространстве) с максимальной размерностью, соответствующем всей системе, классических корреляций нет, но они могут быть между подсистемами в пространствах состояний меньшей размерности. Данное обстоятельство можно пояснить еще следующим образом: гипотетический внешний наблюдатель, который смотрит на замкнутую систему снаружи, не увидит перед собой никаких классических объектов и не обнаружит взаимодействий между ними.
Чистые состояния
квантовомеханических систем определяются
конечным числом собственных функций
некоторого оператора. Например, состояния
с определённой проекцией орбитального
момента на направление магнитного поля,
ориентированного по оси z, определяются
(2l+1) различными функциями
![]() ,
соответствующим различным значениям
,
соответствующим различным значениям![]() =mђ.
В таких случаях произвольное чистое
состояние
=mђ.
В таких случаях произвольное чистое
состояние![]()
![]() изображается линейной суперпозицией
изображается линейной суперпозицией![]() =
=![]() .
Тогда среднее значение физической
величины L в этом состоянии будет
.
Тогда среднее значение физической
величины L в этом состоянии будет![]() ,
где
,
где
![]()
матричный элемент
оператора
![]()
![]()
![]() .
.
Смешанным состоянием называется такое состояние системы, которое не может быть описано одним вектором состояния, а может быть представлено только матрицей плотности.
Если система
находится в смешанном состоянии, т.е. в
состоянии, которому нельзя сопоставить
волновую функцию, то это значит, что мы
«приготовляем» состояние, не определив
максимально возможное число независимых
физических величин, знание которых
необходимо для полного описания с
помощью волновой функции. Например,
состояние неполяризованного пучка
фотонов относится к смешанному состоянию,
которому нельзя сопоставить волновую
функцию. Смешанное состояние можно
рассматривать, как некогерентную смесь
чистых состояний
![]() со статистическим весом
со статистическим весом![]() -действительного положительного числа,
удовлетворяющего условию
-действительного положительного числа,
удовлетворяющего условию
![]() .
.
Понятие «некогерентная смесь» означает, что при вычислении среднего значения <L> физической величины L в смешанном состоянии необходимо определить вероятности значений этой величины в чистых состояниях, т.е. вычислить
![]()
и получить величину среднего, используя статистический вес
<L>=
![]() .
.
Матрица с элементами
![]()
называется матрицей плотности или статистическим оператором, действующим в гильбертовом пространстве. Этот оператор был введён фон Нейманом в 1927 г. Волновая функция тогда это лишь вектор в гильбертовом пространстве.
Матрица плотности определяет данное смешанное состояние квантовой системы. Тогда среднее значение
![]() =
=![]()
или
![]() ,
,
т.е. сумма диагональных элементов матрицы, шпур.
Матрица плотности обладает следующими свойствами:
эрмитовость
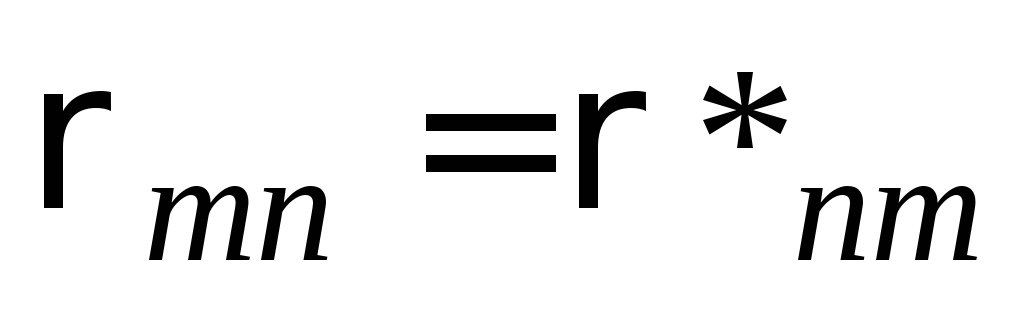 ,
обеспечивает действительность
наблюдаемых величин; любая матрица
плотности должна быть симметричной (в
вещественном случае), ее недиагональные
элементы расположены парами симметрично
относительно главной диагонали. В
комплексном случае эти пары будут
комплексно сопряженными;
,
обеспечивает действительность
наблюдаемых величин; любая матрица
плотности должна быть симметричной (в
вещественном случае), ее недиагональные
элементы расположены парами симметрично
относительно главной диагонали. В
комплексном случае эти пары будут
комплексно сопряженными;нормировка
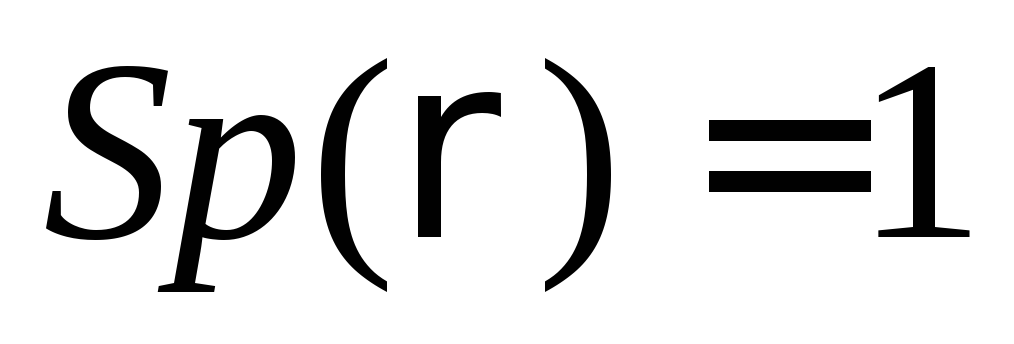 ;
сумма диагональных элементов равна 1;
;
сумма диагональных элементов равна 1;
3. неотрицательность
вероятности
![]() - следствие второго свойства;
- следствие второго свойства;
4. для чистых
состояний
![]() (одно слагаемое в статистическом
усреднении);
(одно слагаемое в статистическом
усреднении);
5. собственные значения матрицы плотности вещественны (нет комплексных чисел) и неотрицательны (больше нуля или равны ему). Для матрицы плотности всегда существует унитарное преобразование, которое приводит ее к диагональной форме, и по диагонали будут стоять неотрицательные вещественные числа. В случае чистых состояний ситуация еще проще — матрица плотности такого состояния имеет только одно ненулевое собственное значение (равное единице), а все остальные равны нулю.
Отличие матрицы плотности чистого и смешанного состояния состоит в следующем: матрица плотности чистого состояния имеет только одно собственное значение, равное единице, в то время как для смешанного состояния у матрицы плотности отличны от нуля несколько собственных значений - т.н. парциальные (т.е. взвешенные с различными вероятностями) населенности соответствующих чистых состояний.
Идемпотентной называется матрица, для которой выполняется условие А2 = А, если оно не выполняется — матрица неидемпотентная. В случае чистого состояния соответствующая матрица (оператор) плотности всегда является идемпотентной, в случае смешанного состояния — неидемпотентной. Открытая система, взаимодействующая со своим окружением, то есть находящаяся с ним в запутанном состоянии, описывается неидемпотентными матрицами плотности.
В квантовой теории есть два качественно различных вида суперпозиции в соответствии с тем, что чистые состояния могут описываться вектором состояния, а смешанные — матрицами плотности. Поэтому и накладываться друг на друга могут либо векторы состояния, либо матрицы плотности.