Файл: деп_тукс_10_11.doc

Ф

Рис. 2.5. Действие последовательности делителей и фазовращателя

Действие фазовращателя можно описать унитарным преобразованием

,

Значит, выходной кубит можно вычислить, применяя последовательно все соответствующие преобразования к кубиту, который был на входе

.

Если на входе имеется только один пучок, например, , т.е.=0. Тогда конечное состояние будет

Для значение кубита определено и равно «0». Длязначение кубита равно «1». Таким образом, фазовый сдвиг может переключать состояние выходного кубита между «0» и «1». В общем случае произвольного сдвига вероятность того, что кубит имеет значение «0» будет, а вероятность того, что кубит имеет значение «1», будет.

2. 4. Перепутывание

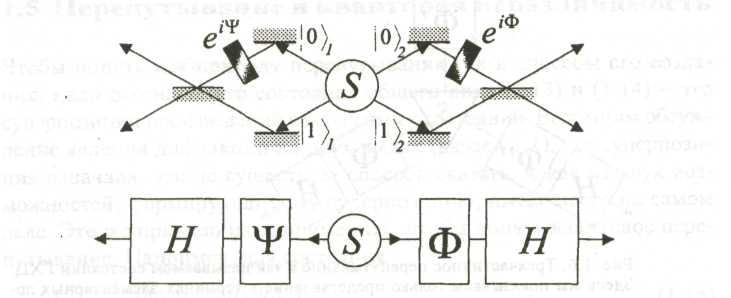
Рис. 2.5. Пример системы, обеспечивающей перепутанные состояния

налево, а другая – направо.

Источник испускает частицы с противоположными импульсами: если частица 1, летящая налево, будет обнаружена в верхнем пучке, то частица 2, летящая направо, будет обязательно обнаружена в нижнем пучке, и наоборот. В понятиях «кубитов» если частица 1 несёт «0», то частица 2 несёт «1», и наоборот. В понятиях квантовой механики это двухчастичное состояние вида

(2.26)

Фаза определяется внутренними свойствами источника, пусть, для простоты,=0. Приведённое перепутанное состояние интересно тем, что ни один из кубитов не несёт определённого значения. Но, как только один из кубитов будет подвергнут измерению, результат которого будет совершенно случаен, то сразу окажется, что другой кубит несёт определённое значение. Вообще, в этом проявляется «загадка» квантовой нелокальности, т.к. во время измерения два кубита могут быть удалены друг от друга на произвольно большое расстояние.

Интересная ситуация возникает, когда оба кубита подвергнуты фазовому сдвигу и преобразованию Адамара. Тогда для детектирования после обоих преобразований Адамара, т.е. в случае проверки с помощью двухчастичного интерферометра для детектирования за делителем, появляются интересные нелокальные корреляции: невозможно объяснить корреляции между явлениями, наблюдаемыми на двух сторонах прибора на основе одних лишь локальных свойств кубитов. Нельзя понять квантовые корреляции между ними, если считать, что на детектор, регистрирующий частицу на одной заданной стороне, не влияет величина фазы для другой частицы, заданной как параметр.

2.5. Перепутывание и квантовая неразличимость

Состояния общего вида

(2.27)

это суперпозиция произведений независимых состояний, означающая вообще, что не существует способа указать, какая из двух возможностей, формирующих эту суперпозицию, имеет место на самом деле. Это же правило надо применить, чтобы понять квантовое перепутывание. Например, для состояния

(2.28)

нет способа указать, несёт ли кубит 1 значение «0» или «1», и, аналогично, несёт ли кубит 2 значение «0» или «1». Но, если измерить один кубит, второй немедленно примет чётко определённое квантовое состояние. Эти заключения приводят к условиям того, как создавать и наблюдать перепутанные квантовые состояния.

Имеется много способов создать перепутанные состояния. Во-первых, можно создать такой источник, что, в силу его физического устройства, появляющиеся квантовые состояния уже будут иметь свойство неразличимости, которое обсуждалось выше. Это реализуется, например, распадом частицы со спином 0 на две частицы со спином ½ с сохранением внутреннего момента импульса. В этом случае спины возникающих частиц должны быть противоположными, и, если нет дальнейших механизмов, позволяющих различить возможности прямо у источника, появляющееся квантовое состояние есть

, (2.29)

где, например, обозначает частицу 1 со спином вверх. Это состояние обладает свойством вращательной инвариантности, т.е. два спина антипараллельны, относительно какого бы направления их не измеряли.

Другая возможность состоит в том, что источник может на самом деле создавать состояния в виде индивидуальных компонент в суперпозиции, но состояния могут быть все равно каким-то образом различимы. Это происходит, например, при параметрическом рассеянии типа-II, где состояния фотонов вдоль определённого выбранного направления равны

и . (2.30)

Это означает, что либо фотон 1 поляризован горизонтально, а фотон 2-вертикально, либо фотон 1 поляризован вертикально, а фотон 2 – горизонтально. Тем не менее, из-за разной скорости света внутри параметрического кристалла-преобразователя для горизонтально и вертикально поляризованных фотонов, временная корреляция между двумя фотонами в этих двух случаях разная. Следовательно, с помощью измерений во времени можно различать два члена и, из-за потенциальной возможности различать эти два случая, не возникает перепутанного состояния. Однако, даже и в такой ситуации можно создать перепутывание, смещая два созданных фотонных волновых пакета друг относительно друга таким образом, чтобы они перестали быть различимыми благодаря своему положению во времени. Фактически это означает применение техники квантового стирания, в которой маркер - в данном случае, относительный порядок во времени - стирается, так что получается состояние с квантовой неразличимостью

,

которое является перепутанным.

Третье средство получить перепутанные состояния – это спроектировать неперепутанное состояние на перепутанное. Перепутанное состояние никогда не ортогонально ни одной из своих компонент. Рассмотрим, например, источник, создающий неперепутанное состояние

.

Предположим, что это состояние проходит через фильтр, описываемый оператором проецирования

,

где - это состояние(7). Тогда появляется следующее состояние

. Оно более не нормировано на единицу, т.к. действие оператора проецирования приводит к потере кубитов.

2.6. Логический элемент «управляемое не»

Ранее обсуждались только однокубитные логические элементы. Для квантовых вычислений важны двухкубитные элементы, в которых эволюция одного кубита зависит от состояния второго. Самый простой из них – это элемент «управляемое НЕ», показанный на рисунке.

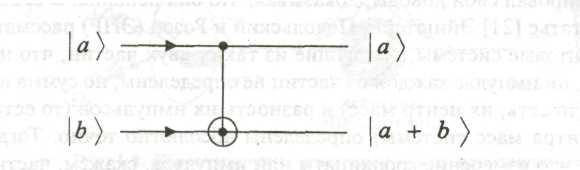
Элемент «управляемое НЕ» - это преобразование, связанное с двумя кубитами. Значение контрольного кубита (на рисунке – вверху) влияет на нижний, чьё значение «переключается» на обратное, если верхний кубит несёт «1», и не меняется, если верхний кубит несёт «0». Иначе, суть его работы в том, что значение так называемого целевого кубита (кубит-мишень) меняется на обратное в том и только в том случае, если контрольный кубит имеет логическое значение «1». Логическое значение контрольного кубита не меняется. Можно описать действие квантового логического элемента «управлямое НЕ» следующими преобразованиями

,

,

где иотносятся к контрольному кубиту, аи- к целевому. Вместе с однокубитными преобразованиями, описанными ранее, квантовый логический элемент «управляемое НЕ» может быть использован для построения квантовых вычислительных сетей. Одно из интересных приложений этих элементов состоит в создании с их помощью двухкубитных и многкубитных перепутанных состояний.