Файл: деп_тукс_10_11.doc

Однако определение (2.24) не совсем удобно в практическом плане. Для нас привычнее иметь дело с аддитивными величинами, когда информация составной системы равняется сумме частичных информаций. А согласно определению (2.24), информация не суммируется, а перемножается. Так, для двусоставной системы (в случае некоррелированного, то есть сепарабельного состояния)

I_AB = Sp(ρ_АВ)² = Sp(ρ_А)² Sp(ρ_В)² = I_A  I_B.

Поэтому удобнее перейти к логарифму от этой величины. Поскольку логарифм произведения равен сумме логарифмов сомножителей, получается аддитивность. При этом ln[Sp(ρ²)] изменяется в пределах от –lnd до 0.

Из статистической механики известно, что на больших временах энтропия системы соответствует среднему значению –k lnρ, где k — постоянная Больцмана, так что согласно (2.25) имеем:

<–k lnρ > = –k Sp(ρ lnρ)

Отсюда связь между количеством информации в системе и энтропией

Sp(ρ lnρ) = <lnρ>,

которая называется энтропией фон Неймана и чаще всего используется сейчас в качестве меры квантовой информации. Она и была введена в качестве первой меры квантовой запутанности. Различие между натуральным логарифмом и логарифмом по основанию 2 в данном случае не принципиально.

Заметим, что Sp(ρ lnρ) и ln[Sp(ρ²)] изменяются в одних и тех же пределах и никогда сильно не отличаются друг от друга. Однако при использовании этой меры, чтобы получить положительное число, приходится в выражениях ставить знак минус. При этом иногда забывается, что при переходе к логарифму с информацией произошел своеобразный «перевертыш»: там, где был минимум информации, — теперь стал максимум, а максимум информации (единица для чистого состояния) обратился в нуль. Хотя и эту ситуацию можно трактовать так, что, с точки зрения внешнего наблюдателя, о чистом состоянии он ничего не может сказать, поскольку это замкнутая система, которую наблюдатель еще не «потревожил» своим измерением.

Квантовая теория информации, таким образом, непосредственно связывает информацию с энергией через энтропию фон Неймана, которую можно считать основной физической характеристикой энергоинформационного процесса. Изменение информации сопровождается изменением энергии, а обмен информацией напрямую связан с обменом энергией (справедливо и обратное) — это еще один важный вывод, который сделан в физике квантовой информации.

Есть и отдельные строгие результаты, связывающие информацию, энергию и энтропию. В частности, теорема Марголюса-Левитина утверждает, что число элементарных логических операций, которые физическая система может выполнить в единицу времени, ограничено энергией системы, а количество информации, которую система может зарегистрировать (воспринять), ограничено ее собственной максимальной энтропией.

Прямая связь между энергией и выполняемыми логическими операциями (информационными процессами) позволяет перекинуть мостик к физическим процессам, сопровождающим работу сознания, поскольку она непосредственно связана с логическими операциями.

Информация в терминах энтропии фон Неймана позволяет описывать запутанные состояния. Одна из основных особенностей этого понятия состоит в том, что об объекте, находящемся в чистом запутанном состоянии (ρ = ρ²), невозможно получить никакой информации, поскольку в этом случае S(ρ) = 0. Энтропия фон Неймана и квантовая запутанность может быть отлична от нуля только для подсистем, которые взаимодействуют со своим окружением, и поэтому находятся в несепарабельном состоянии.

Довольно часто для простоты количество квантовой информации определяется просто как число кубитов в системе.

Исходная величина Sp(ρ²) сейчас тоже широко используется в физике квантовой информации, но уже не в качестве меры информации, а как характеристика степени чистоты состояния, которая показывает, насколько близко данное состояние к чистому, для последнего Sp(ρ²) = 1.

2. 3. Преобразование одного кубита

Одно из основных преобразований в квантовой теории информации – это преобразование Адамара. Оно действует на кубит следующим образом:

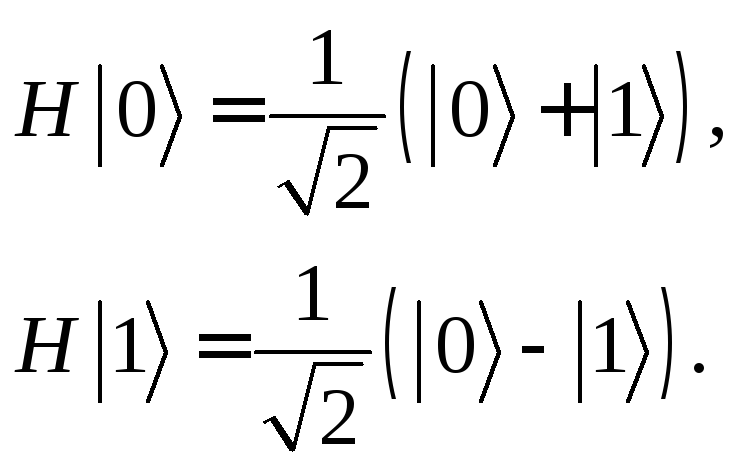
Применив, например, его к кубиту

|

получим

т.е. строго определённое значение кубита. Это было бы невозможно сделать с некогерентной смесью.

Рассмотрим действие простого делителя, делящего луч в отношении50/50. Такие делители были реализованы не только для фотонов. Пусть имеется две входящие и две выходящие моды.

вход

|0>_in

1

H

2

|1>_in

Рис. 2.3. Действие простого делителя

Частица, падающая сверху или снизу на такой делитель, появится либо в верхнем, либо в нижнем выходящем луче с одной и той же вероятностью 0,5. Д

,

Фазовое действие делителя будет описываться преобразованием Адамара.

Предположим, что состояние на входе – произвольный кубит

Для одной частицы это означает, что -это амплитуда вероятности обнаружить частицу, падающую на делитель сверху, а- амплитуда обнаружить частицу, падающую снизу. Тогда в результате действия делителя, получается конечное состояние

,

так что амплитуда вероятности найти частицу в верхнем выходящем пучке равна , а амплитуда вероятности найти её в нижнем пучке равна. В частности, если

или =0, то частицу с равной вероятностью можно обнаружить в любом из выходящих пучков. В случае жечастица будет обязательно обнаружена в верхнем пучке и никогда не будет обнаружена в нижнем пучке.

Рассмотрим последовательность таких делителей, осуществляющих последовательность преобразований Адамара. Используется интерферометр Маха-Цандера с двумя одинаковыми делителями

|0>_out

|0>_in

|1>_in

З2

Н

Рис. 2.4. Действие последовательности делителей и двух преобразований Адамара

В данном случае зеркала нужны только для того, чтобы перенаправить пучки. Действие интерферометра как последовательность двух последовательных преобразований Адамара представляется в виде:

Результат прямо следует из того факта, что двойное действие преобразования Адамара есть тождественное преобразование - на выходе интерферометра воспроизводится входное состояние. В частном случае, когда на входе имеется только одно состояние ( = 1,  = 0), на выходе частица будет обнаружена в верхнем пучке, хоть и внутри интерферометра эта частица имеет одинаковые вероятности оказаться в каждом из плеч. Дело в том, что выходные амплитуды вероятностей определяются относительной фазой, набегающей в интерферометре. В оптике этот эффект изучен досконально и не вызывает удивления. С массивными частицами, поведение которых можно описывать волнами де Бройля дело происходит точно также.

На языке теории квантовой информации рассмотренный эффект формулируется так: кубит на выходе интерферометра имеет определенное значение, если и только если кубит на входе имеет определенное значение, внутри интерферометра его состояние максимально неопределенно.

Кроме элемента Адамара важным квантовым логическим элементом является фазовращатель Ф. Его действие состоит в том, чтобы вносить сдвиг фаз у одного из пучков (будем считать, что это происходит в нижнем пучке, хотя это не важно - важна только относительная фаза).

|0>_in

e^i

|1>_in

З2

Н