ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.08.2024
Просмотров: 354
Скачиваний: 0
СОДЕРЖАНИЕ
Теории управления квантовыми системами.
1. Основные понятия и определения квантовой механики
1.1. Чистые и смешанные состояния
2. Элементы квантовой теории информации
2. 3. Преобразование одного кубита
2.5. Перепутывание и квантовая неразличимость
2.6. Логический элемент «управляемое не»
3. Парадокс эйнштейна – подольского – розена (эпр)
5.4 Понятие о квантовой криптографии
5.4.1. Защита посредством неортогональных состояний
5.4.2. Защита посредством перепутывания
5.4.3. Практическая реализация квантово – криптографических систем
6.2. Протокол квантовой телепортации
6. 3. Обзор некоторых экспериментальных результатов по квантовой телепортации
6.4. Заключительные замечания: возможна ли телепортация макрообъекта?
7. Квантовые вычисления. Квантовые компьютеры.
7.4.2. Моделирование вероятности
7.4.3. Алгоритм разложения на простые множители или алгоритм Шора
7.5. Общие требования к квантовым компьютерам Практическая реализация
Квантовая логика сейчас еще только разрабатывается, и пока трудно оценить все возможные последствия нового мышления, но одно несомненно — они будут очень значительны.
В этом отношении многое делается математиками, которые сейчас интенсивно работают над квантовыми алгоритмами и программами для квантового компьютера. Им в какой-то мере проще — не надо думать о физических ограничениях «на железо». Как только появится квантовый компьютер «в железе», у математиков уже будет в запасе большое количество готовых квантовых алгоритмов и программ.
Для реализации квантовых алгоритмов нужно небольшое число логических квантовых операторов (гейтов): однокубитные — NOT (логическое «Не»), преобразование Адамара (перевод кубита в нелокальное суперпозиционное состояние); двухкубитные — CNOT (контролируемое «Не»), SWAP (обмен состояниями) — и этого будет достаточно. С их помощью можно реализовать любые алгоритмы — не только классические, но и квантовые, которые реализуют квантовую логику.
Перечислим известные к настоящему времени квантовые алгоритмы.
Алгоритм Саймона или задача “Оракула”, 1997г. (экспоненциальное время при классических вычислениях и квадратичное время при квантовых). Он также известен под названием “алгоритм Дойча” (1985) и, наверное, является первым квантовым алгоритмом. Этот алгоритм решает задачу определения типа функции, глядя только на результат ее действия.
Алгоритм разложения на простые множители или алгоритм Шора, 1994 г. Для факторизации L - битового числа N лучший классический алгоритм асимптотически дает время
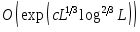 .
Квантовый метод дает асимптотически
.
Квантовый метод дает асимптотически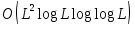 шагов. Заметим, что функция
шагов. Заметим, что функция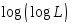 растет чрезвычайно медленно, поэтому
можно считать, что квантовый метод дает
растет чрезвычайно медленно, поэтому
можно считать, что квантовый метод дает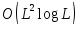 .
Ключевая идея этого алгоритма -
определение периода некой последовательности
с помощью Фурье - преобразования. Период
этой последовательности экспоненциально
зависит отL,
поэтому такой метод непрактичен для
обычных классических вычислений.
.
Ключевая идея этого алгоритма -
определение периода некой последовательности
с помощью Фурье - преобразования. Период
этой последовательности экспоненциально
зависит отL,
поэтому такой метод непрактичен для
обычных классических вычислений. Алгоритм поиска в базе данных (“алгоритм Гровера” 1997г.). Имеется список из N наименований. Классический алгоритм дает порядка N/2 обращений к базе данных для отыскания нужного наименования. Квантовый требует порядка
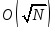 обращений. Например, еслиN
= 104,
классический метод дает ответ примерно
за 5000 обращений, а квантовый - за 100. Если
же N
= 106,
то классический поиск потребует 5х105
обращений, а квантовый метод всего
1000!
обращений. Например, еслиN
= 104,
классический метод дает ответ примерно
за 5000 обращений, а квантовый - за 100. Если
же N
= 106,
то классический поиск потребует 5х105
обращений, а квантовый метод всего
1000!
7.4.1. Моделирование времени.
Для этого алгоритма потребуется ввести дискретизацию времени. Известно, что при физических измерениях не может быть достигнута бесконечная точность, поэтому потребуем дискретизацию в масштабах 10-27сек. При необходимости эта величина может быть сделана еще меньше!
Один из способов
моделирования времени состоит в том,
что компьютер переходит от состояния
к состоянию, например, в модели клеточных
автоматов. Такое требование не противоречит
нашей интуиции о ходе времени - мы
переходим от одного состояния к другому.
В этом смысле время невозможно моделировать
вообще, как в модели клеточного автомата,
его можно лишь имитировать (есть очевидная
разница между имитацией и моделированием
- полет шмеля может имитировать каждый,
но далеко не каждый знает, как построить
модель, описывающую этот процесс).
Согласно модели клеточного автомата
пространство разбивается на набор
клеток; есть правило изменения величины,
записанной в каждой клетке; состояния
в каждой клетке меняются одновременно
при каждом следующем шаге. Тогда возникает
следующий вопрос - можно ли время
моделировать, а не имитировать? Представим
себе мир с пространственно-временной
точки зрения, т.е. когда представляющие
точки распределены в пространстве и
времени (заглядывая вперед во времени).
Тогда мы могли бы сказать, что компьютер
работает по правилу: состояние si
в пространственно-временной точке
дается функцией
![]() ,
определенной в некоторых соседних сi
точках.
,
определенной в некоторых соседних сi
точках.
sj
Время
si







sk



пространство




Видно, что если эта функция устроена так, что ее значение в точке i зависит от значения в нескольких точках, находящихся позади во времени (т.е. в более ранние моменты), то мы просто должны переопределить описание клеточного автомата. Это так, поскольку вы вычисляете какое-то значение в точке i на основе значений в предыдущих точках, а тех - опять в предыдущих точках, значит можно вычислить все следующие значения, двигаясь в определенном порядке. Но можно представить себе более сложную модель компьютера, работающего с более общим классом функций - обобщенных связей между пространственно-временными точками. Если F зависит от всех точек как в прошлом, так и в будущем, что будет в этом случае? Как в этом случае можно представить действие физических законов?
Замечено, что во многих физических теориях соответствующие математические уравнения сильно упрощаются, если, скажем, частицам, разрешается двигаться назад во времени (электрон - позитрон) или вообще существуют связи, соединяющие прошлое и будущее объектов. Можно ли в этом случае построить компьютер, работающий по такому алгоритму? Предположим, что мы знаем такую функцию Fi и эта функция зависит, в том числе, от переменных, расположенных в будущие моменты времени. Как тогда упорядочить данные, чтобы они автоматически удовлетворяли упомянутым выше уравнениям? Может статься, что это вообще невозможно. В случае клеточного автомата это возможно, поскольку из данного ряда можно получить следующий ряд, и затем опять следующий ряд и т.д. - т.е. мы указали способ, как это сделать.
Классическая физика удовлетворяет принципу причинности. Можно, в терминах информации в прошлом, если задействовать координату и импульс или два значения координаты в разные моменты времени (нужно обладать двумя кусочками информации в каждой точке), вычислить будущее, хотя бы в принципе. Поэтому классическая физика локальна, причинна и обратима, с очевидностью, вполне пригодна для компьютерного моделирования. Здесь нет никаких проблем.
7.4.2. Моделирование вероятности
Говоря о квантовой механике, мы признаем, что здесь имеем дело лишь возможностью предсказывать вероятности.
Один из способов получить компьютер, моделирующий вероятностные теории - описание чего-то, что происходит с определенной вероятностью, - это рассчитать эту вероятность и интерпретировать полученное число для представления реальности. Например, предположим, что частица имеет вероятность P(x, t) находиться в точке х во время t. Типичный случай - когда вероятность удовлетворяет дифференциальному уравнению, например уравнению:
![]() .
.
Теперь можно
дискретизировать время и координату,
а, возможно, и саму вероятность и решать
это дифференциальное уравнение так,
как обычные уравнения теории поля,
создавая для этого алгоритм, работающий
в дискретной модели. Во-первых, здесь
появляется проблема с дискретизацией
вероятности. Если ограничиться к
цифрами (разрядами), это означает, что
когда вероятность какого-нибудь события
становится меньше чем 2-к
, то мы говорим, что этого никогда не
произойдет. На практике, так оно и есть.
Если вероятность события меньше, чем
10-20,
мы говорим, что оно никогда не произойдет
или не будет происходить слишком часто.
Но на самом деле здесь имеется определенная
трудность. Если мы рассматриваем много
частиц, скажем, R
в системе, то мы должны описывать
вероятность при условии, что частицы
находятся в точках
![]() в моментt.
Так описывается вероятность для системы.
Поэтому нам нужно к-разрядное
число для каждой конфигурации системы,
для каждой из R
“конфигураций” величины х.
Поэтому, если у нас есть N
пространственных точек (в смысле
клеточного автомата), нам необходимо
описать NR
конфигураций. На самом деле мы считаем,
что в каждой точке пространства имеется
информация типа электрического поля и
т.п., поэтому R
окажется такого же порядка что и N,
если количество информации, выраженное
в битах, совпадает с числом точек в
пространстве. Следовательно, мы получаем
порядка NN
конфигураций, которое необходимо
описать, для того чтобы получить
вероятность. Значит, эта величина
окажется гораздо большей, чем размер
нашего компьютера, который порядка N.
в моментt.
Так описывается вероятность для системы.
Поэтому нам нужно к-разрядное
число для каждой конфигурации системы,
для каждой из R
“конфигураций” величины х.
Поэтому, если у нас есть N
пространственных точек (в смысле
клеточного автомата), нам необходимо
описать NR
конфигураций. На самом деле мы считаем,
что в каждой точке пространства имеется
информация типа электрического поля и
т.п., поэтому R
окажется такого же порядка что и N,
если количество информации, выраженное
в битах, совпадает с числом точек в
пространстве. Следовательно, мы получаем
порядка NN
конфигураций, которое необходимо
описать, для того чтобы получить
вероятность. Значит, эта величина
окажется гораздо большей, чем размер
нашего компьютера, который порядка N.