Добавлен: 28.11.2018
Просмотров: 3569
Скачиваний: 53
21
Тема 3. Основные вопросы эксплуатационной надёжности тех-
нических систем
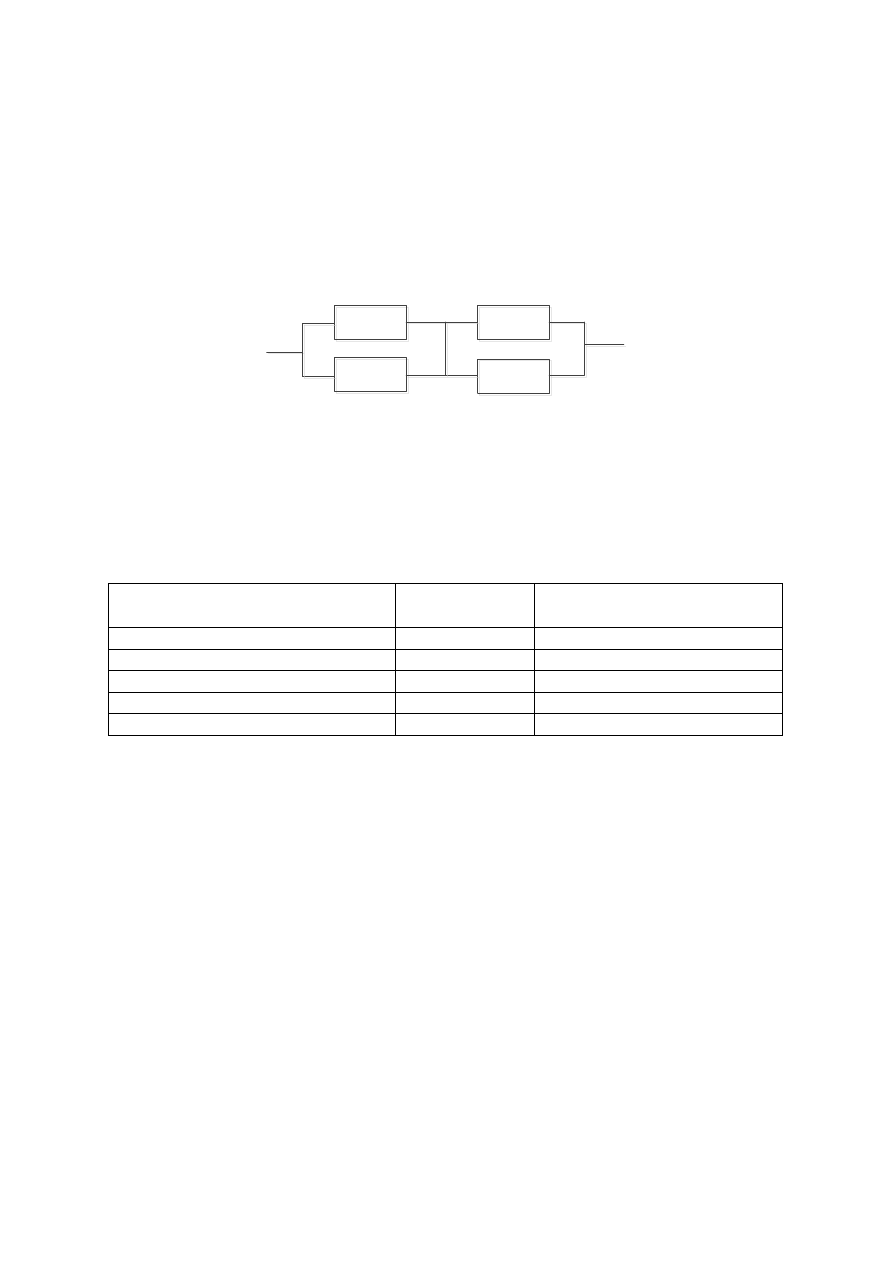
8. Схема расчета надежности устройства приведена на рис 5.3.
Предполагается, что последействие отказов отсутствует и все элементы
расчета равнонадежны. Интенсивность отказов элемента
3
1,15 10
1/ч.
Определить наработку до первого отказа устройства.
λ
λ
λ
λ
Рис. 5.3. Структурная схема надёжности системы
9. Для повышения надежности автоматической линии (АЛ) каж-
дый её станок дублирован и вступает в работу при отказе основного
станка. Состав элементов нерезервированной линии и данные по
интенсивности отказов элементов приведены в табл. 5.3.
Таблица 5.3
Элементы АЛ
Количество
элементов
Интенсивность отказов
элемента,
5
10
(1/ч)
Многошпиндельный токарный п/а
3
2,16
Горизонтально-фрезерный станок
2
0,78
Вертикально-сверлильный станок
1
0,32
Круглошлифовальные п/а
1
0,09
Внутришлифовальный п/а
2
0,23
Предполагается, что имеет место экспоненциальный закон надеж-
ности, станки подвержены лишь одному виду отказов и последействие
отказов отсутствует. Найти вероятность безотказной работы линии
в течение 1000 час.
10. Для повышения точности измерения некоторой величины при-
менена схема группирования приборов из пяти по три, т.е. результат
измерения считается верным по показанию среднего (третьего) прибора.
Требуется найти вероятность безотказной работы Р
c
(t), среднее время
безотказной работы T такой системы, а также частоту отказов f
c
(t) и ин-
тенсивность отказов λ
c
(t) системы, если интенсивность отказов каждого
прибора λ(t) = 0,4·10
–3
1/ч.

22
Тема 4. Диагностика автоматизированных систем
11. При испытаниях партии исполнительных механизмов (ИМ) из
6 штук было установлено, что погрешность позиционирования со време-
нем увеличивается. Данные о погрешностях, полученные для моментов
времени эксплуатации t
1
= 0 ч, t
2
= 40 + 10·N ч приведены в табл. 5.2.
Таблица 5.2
Номер ИМ
1
2
3
4
5
6
[мм] при t = 0 ч
0,19
0,16
0,23
0,18
0,11
0,21
[мм] при t = 40 + 10·N ч
0,28
0,18
0,26
0,24
0,19
0,22
Для использования ИМ в задвижках нефтепровода необходимо,
чтобы погрешность его позиционирования была ∆ ≤ 0,25 мм.
Полагая, что скорость изменения погрешности подчиняется нор-
мальному закону распределения, определите интервал проведения про-
филактических работ для ИМ данного типа, исключающий их посте-
пенные отказы с вероятностью
.
95
,
0
P
12. Рассчитать время проведения профилактического ремонта си-
стемы управления, имеющей значение главного параметра
5
,
6
0
X
, до-
пуск на параметр (
0,4), среднеквадратичное отклонение
35
,
0
σ
0
, ес-
ли известно, что
t
t
t
m
t
m
08
,
0
σ
)
(
σ
,
5
,
0
)
(
0
0
, а в момент начала
проведения
профилактических
работ
требуемая
вероятность
92
,
0
)
(
проф
t
P
.
13. Устройство состоит из четырёх групп элементов, в каждой из кото-
рых, соответственно, N
1
= 30, N
2
= 20, N
3
= 15, N
4
=18 элементов с интенсив-
ностями отказов
4
1
10
5
,
2
λ
ч
–1
,
4
2
10
5
,
1
λ
ч
–1
,
4
3
10
8
λ
ч
–1
,
4
4
10
5
,
5
λ
ч
–1
.
Элементы 2 и 3 групп восстанавливаемы со временем восстановле-
ния
30
τ
2
В
ч,
40
τ
3
В
ч. Пополнение элементов 1 и 4 групп в ЗИПе
проводится через 400 часов.
Определите, сколько элементов каждой группы должно быть
в ЗИПе, чтобы его достаточность была не менее 0,9?

23
Вариант 6
Тема 1. Расчет надёжности систем
1. За наблюдаемый период эксплуатации в аппаратуре было за-
фиксировано 7 отказов. Время восстановления составило: t
1
= 12 мин,
t
2
= 23 мин, t
3
= 15 мин, t
4
= 9 мин, t
5
= 17 мин, t
6
= 28 мин, t
7
= 25 мин,
t
8
= 31 мин. Требуется определить среднее время восстановления аппа-
ратуры T
В
*.
2. Вероятность безотказной работы изделия в течение t = 1000 ч.
P(1000) = 0,95. Время исправной работы подчинено закону Релея. Тре-
буется определить количественные характеристики надежности λ(t),
a(t), T.
3. По результатам испытания 300 приводов исполнительных меха-
низмов, проводившихся без замен и отказавших в течение 1 000 часов,
были получены данные о наработках до отказа, приведённые в табл. 6.1.
Вычислить значения и построить графики вероятности безотказной
работы, интенсивности отказов, частоты отказов приводов исполни-
тельных механизмов.
Таблица 6.1
Интервалы наработки
, ч
i
t
0–100 100–200 200–400 400–600 600–800 800–1000
Число отказов
i
n t
90
80
70
30
10
20
4. На насосной станции магистрального трубопровода установлены
3 насоса, наработка до отказа которых определяется нормальным зако-
ном распределения с параметрами:
насос 1: m
1
= 2500 ч, σ
1
= 1900 ч;
насос 2: m
2
= 2800 ч, σ
2
= 1900 ч;
насос 3: m
3
= 4500 ч, σ
3
= 2300 ч.
Время безотказной работы системы управления насосами опреде-
ляется законом Рэлея с параметром λ
С
= 0,00025 ч
–1
. Определите, какова
будет вероятность безотказной работы манипулятора через неделю не-
прерывной работы в три смены?
5. Установлено, что наработка до отказа привода задвижки имеет
распределение Вейбулла с параметром α = 1,1. Вероятность безотказной
работы привода в течение наработки (0, 250) часов равна 0,96. Требует-
ся определить интенсивность отказов в момент времени t = 250 ч,
и среднюю наработку до отказа привода.
24
Тема 2. Обеспечение заданного уровня надёжности технических
систем
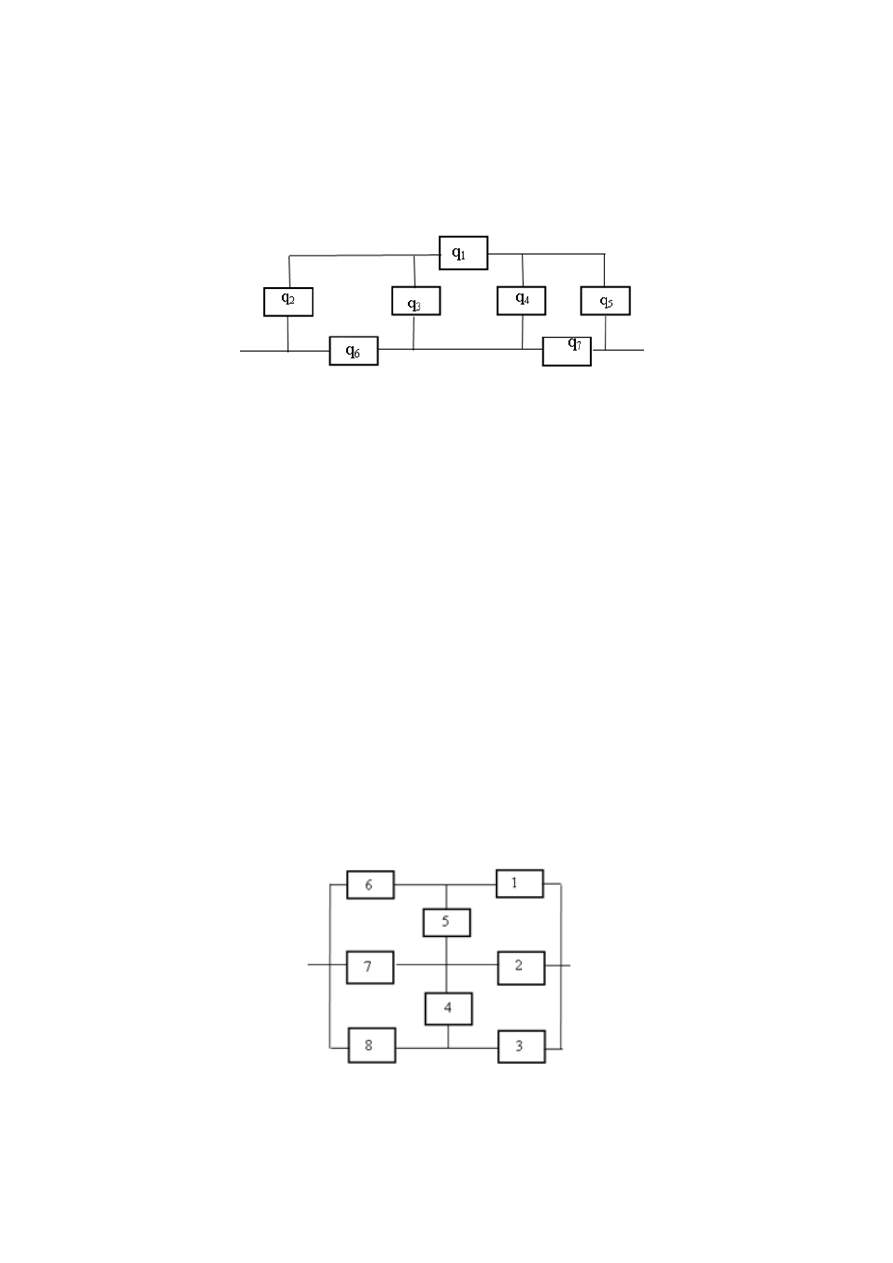
6. Структурная схема надёжности системы имеет вид «сложного
мостика», показанного на рис 6.1.
Рис. 6.1. Структурная схема надёжности системы
Для элементов 1, 5:
4
1
,
2 10
ч ,
0,4;
t
P t
e
3, 6:
2
4
1
,
9 10
ч
t
P t
e
.
Элемент 4 имеет нормальное распределение времени безотказной
работы с параметрами
2500 ч,
100 ч;
t
t
m
элементы 2 и 7 имеют
экспоненциальное распределение с интенсивностью
4
1
2
1,5 10 ч ,
5
1
7
6,5 10
ч .
Определите вероятность безотказной работы системы в момент
времени t = 2000 часов.
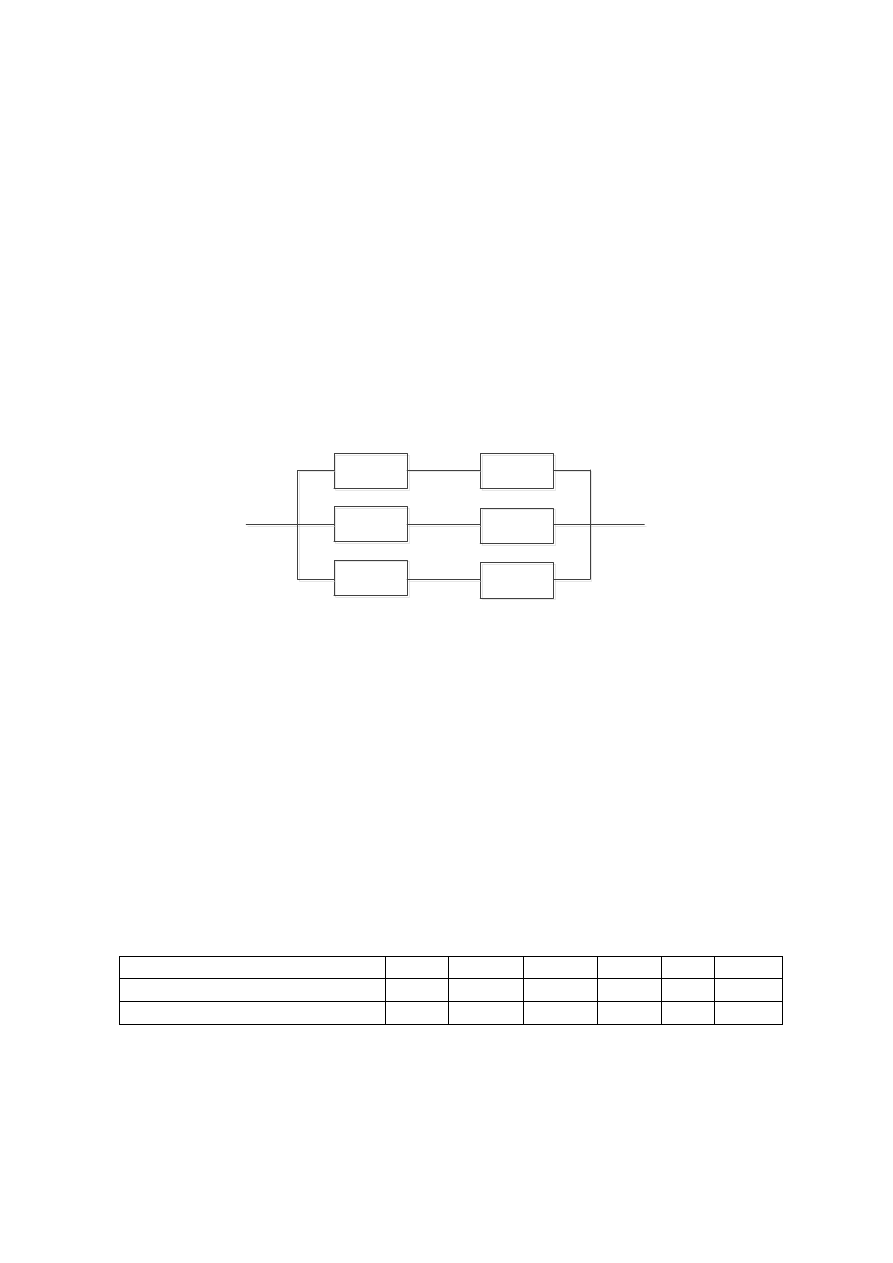
7. Найти вероятность безотказной работы за время наработки
в 300 часов системы, имеющей структурную схему надежности
(рис. 6.2), если для звеньев 1, 2, 3, 4, 5, 6
95
,
0
P
. Для звена 7 веро-
ятность безотказной работы определяется по закону Вейбулла с пара-
метрами
0,4
;
1
0,005 ч ;
для звена 8 – по закону Рэлея с пара-
метром
3
1
5,5 10
ч
.
Рис. 6.2. Структурная схема надёжности системы
25
Тема 3. Основные вопросы эксплуатационной надёжности тех-
нических систем
8. Система состоит из двух блоков, соединенных последовательно
и характеризующихся соответственно интенсивностями отказов
6
1
120,54 10
1/ч и
6
2
185,66 10
1/ч. Выполнено пассивное общее
резервирование с неизменной нагрузкой всей системы (блока 1 и 2).
Требуется определить вероятность безотказной работы системы P
с
(t),
частоту отказов a
с
(t), среднее время безотказной работы системы T
0
и интенсивность отказов λ
с
(t). Определить P
с
(t) при t = 20 ч.
9. Схема расчета надежности изделия приведена на рис 6.3. Найти
вероятность безотказной работы изделия, если известны вероятности
отказов элементов: Q
1
= 0,003, Q
2
= 0,09.
Q
1
Q
1
Q
1
Q
2
Q
2
Q
2
Рис. 6.3. Структурная схема надёжности системы
10.
Наработка реле регулятора стеклоочистителя до отказа имеет
гамма-распределение с параметрами k = 3 и λ
0
= 0,05. Определить веро-
ятность безотказной работы реле и интенсивность отказов при наработ-
ке, равной 24 часам.
Тема 4. Диагностика автоматизированных систем
11. При испытаниях партии исполнительных механизмов (ИМ) из
6 штук было установлено, что погрешность позиционирования со време-
нем увеличивается. Данные о погрешностях, полученные для моментов
времени эксплуатации t
1
= 0 ч, t
2
= 55 + 13·N час приведены в табл. 6.2.
Таблица 6.2
Номер ИМ
1
2
3
4
5
6
[мм] при t = 0 ч
0,15
0,13
0,19
0,11
0,10
0,14
[мм] при t = 55 + 13·N ч
0,18
0,14
0,20
0,19
0,18
0,15
Для использования ИМ в задвижках нефтепровода необходимо,
чтобы погрешность его позиционирования была ∆ ≤ 0,18 мм.