ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2020
Просмотров: 462
Скачиваний: 2
Т е с т Л ь ю и н г а — Б о к с а
Статистика Льюинга-Бокса имеет вид:
Q
p
=
n
(
n
+
2
)
∑
τ=
1
p
r
2
( τ)
n
− τ
, где
τ = 1, 2, ... ,p
;
r(τ)
- выборочный коэффициент автокорреляции.
r
( τ)=
(
n
−τ)⋅
∑
t
=
1
n
− τ
y
t
y
t
+ τ
−
∑
t
=
1
n
− τ
y
t
⋅
∑
t
=
1
n
− τ
y
t
+ τ
√
(
n
−τ)⋅
∑
t
=
1
n
− τ
y
t
2
−(
∑
t
=
1
n
− τ
y
t
)
2
√
(
n
−τ)⋅
∑
t
=
1
n
−τ
y
t
+ τ
2
−(
∑
t
=
1
n
−τ
y
t
+ τ
)
2
Если верна гипотеза
H
0
о равенстве нулю всех коэффициентов автокорреляции,
то статистика
Q
p
имеет распределение
χ
2
с
p
степенями свободы.
Следовательно, если
Q
p
>χ
α
, p
2
, то гипотеза о наличии автокорреляции принимается.
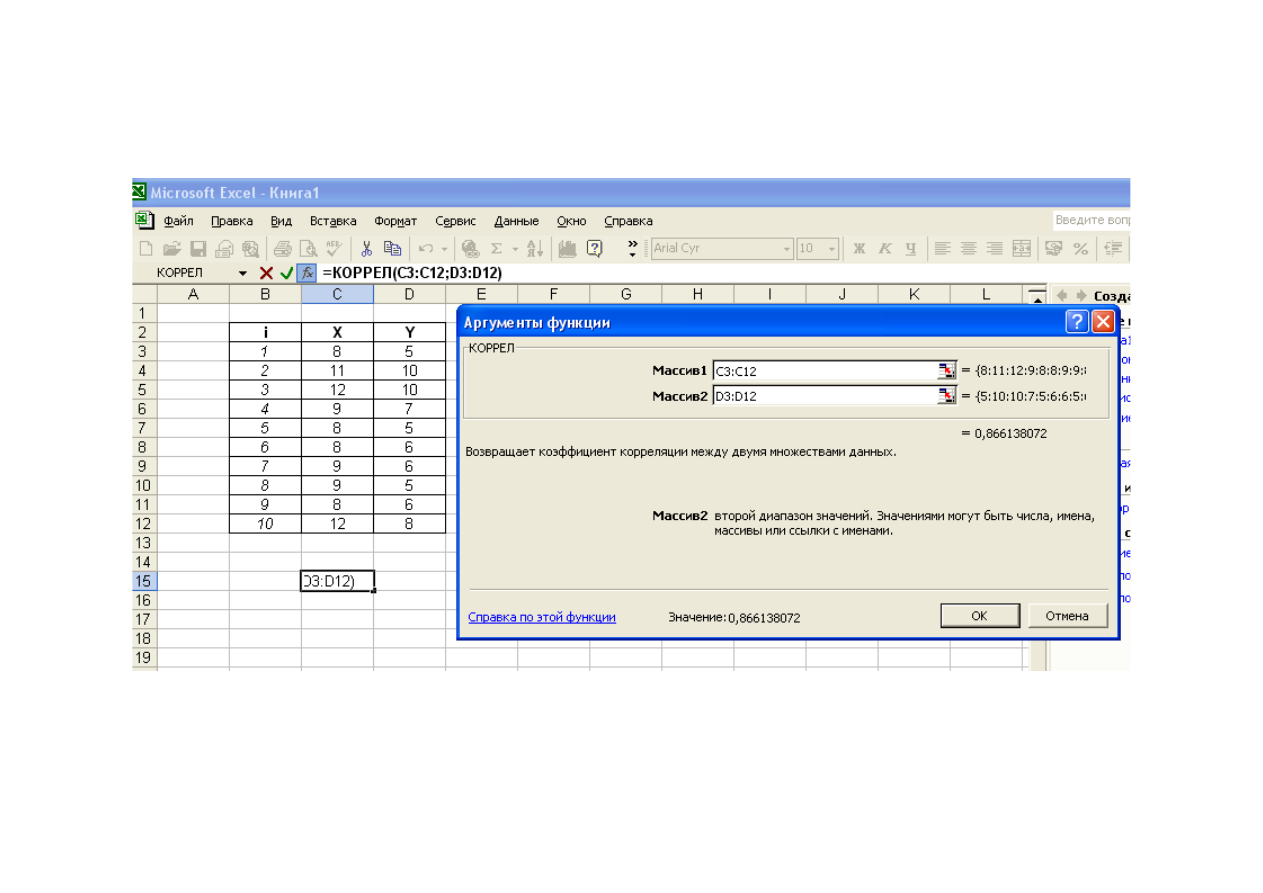
Э к о н о м е т р и ч е с к и е р а с ч е т ы в E x c e l
Вычисление коэффициента корреляции
Э к о н о м е т р и ч е с к и е р а с ч е т ы в E x c e l
Построение корреляционного поля
Э к о н о м е т р и ч е с к и е р а с ч е т ы в E x c e l
Построение корреляционного поля
Э к о н о м е т р и ч е с к и е р а с ч е т ы в E x c e l
Вычисление параметров уравнения парной линейной регрессии