Файл: 1. Классификация признаков данных (Качественные и количественные, непрерывные и дискретные). Номинальные, порядковые, интервальные, дихотомические, относительные переменные.docx

К оглавлению

Алгоритм Naïve Bayes (Наивный Байесовский классификатор) используется для решения задач классификации, когда нужно отнести объекты к определенным категориям, основываясь на значениях их признаков. Он находит широкое применение в областях, таких как анализ текстов, фильтрация спама, распознавание рукописных символов и др.

Теорема Байеса - это математическая формула, которая описывает вероятность наступления события A при условии наступления события B. Формула выглядит следующим образом:



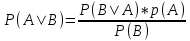
где P(A|B) - вероятность того, что событие A произойдет при условии, что событие B произошло;

P(B|A) - вероятность того, что событие B произойдет при условии, что событие A произошло;

P(A) и P(B) - соответственно, вероятности событий A и B.

Суть теоремы Байеса заключается в том, что она позволяет пересчитывать вероятности на основе новой информации. Например, если мы знаем вероятность заболевания определенной болезнью, то мы можем использовать теорему Байеса, чтобы вычислить вероятность заболевания при наличии некоторых симптомов.

Алгоритм Naïve Bayes является «наивным», потому что он предполагает, что все признаки независимы друг от друга. То есть, например, в задаче классификации текстов он предполагает, что появление каждого слова не зависит от появления других слов в тексте. Это, конечно, не всегда верно, но на практике такой подход часто работает достаточно хорошо и дает высокую скорость обучения и классификации.

В задаче фильтрации СПАМ-сообщений мы можем использовать алгоритм Naïve Bayes для определения, является ли сообщение СПАМом или нет. Для этого мы обучаем модель на наборе текстовых данных, которые размечены как СПАМ или не СПАМ, и вычисляем априорные вероятности для каждого класса. Затем мы извлекаем признаки из нового сообщения, например, количество вхождений определенных слов, и используем модель, чтобы вычислить вероятности для каждого класса. Например, если вероятность, что сообщение является СПАМом, больше, чем вероятность, что оно не является СПАМом, то мы классифицируем его как СПАМ.

---

23. Машина опорных векторов. Для решения каких задач применяется алгоритм? Объясните смысл алгоритма. Понятие гиперплоскости. Напишите наиболее распространенные ядерные функции.

К оглавлению
Машины опорных векторов — семейство алгоритмов бинарной классификации, основанных на обучении с учителем, использующих линейное разделение пространства признаков с помощью гиперплоскости.

Основная идея метода заключается в отображение векторов пространства признаков, представляющих классифицируемый объекты, в пространство более высокой размерности. Это связано с тем, что в пространстве большей размерности линейная разделимость множества оказывается выше, чем в пространстве меньшей размерности. Причины этого интуитивно понятны: чем больше признаков используется для распознавания объектов, тем выше ожидаемое качество распознавания.

После перевода в пространство большей размерности, в нём строится разделяющая гиперплоскость. При этом все векторы, расположенные с одной «стороны» гиперплоскости, относятся к одному классу, а расположенные с другой — ко второму. Также, по обе стороны основной разделяющей гиперплоскости, параллельно ей и на равном расстоянии от неё строятся две вспомогательные гиперплоскости, расстояние между которыми называют зазор.

Задача заключается в построении разделяющей гиперплоскость таким образом, чтобы максимизировать зазор — область пространства признаков между вспомогательными гиперплоскостями, в которой не должно быть векторов. Предполагается, что разделяющая гиперплоскость, построенная по данному правилу, обеспечит наиболее уверенное разделение классов и минимизирует среднюю ошибку распознавания.

Векторы, которые попадут на границы зазора (т.е. будут лежать на вспомогательных гиперплоскостях), называют опорными векторами
Гиперпло́скость — подпространство коразмерности 1 в векторном, аффинном пространстве или проективном пространстве; то есть подпространство с размерностью, на единицу меньшей, чем объемлющее пространство

Обобщением понятия плоскости трехмерного пространства на случай n -мерного пространства является понятие гиперплоскости

---

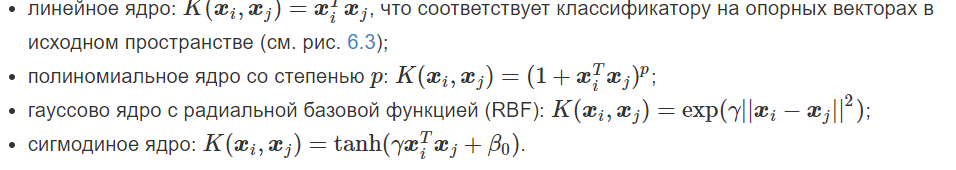
24. Алгоритм решающего дерева. Для решения каких задач применяется алгоритм? Объясните смысл алгоритма. Из чего состоит дерево решений? Формула прироста информации. Напишите формулы для критериев информативности при решении задачи классификации. Какая функция потерь чаще всего используется при решении задачи регрессии.
К оглавлению

https://mcs.mail.ru/blog/kak-sozdat-idealnoe-derevo-reshenij

При решении задач регрессии в качестве функции потерь используют среднюю квадратическую ошибку (MSE). Это разница между прогнозируемым значением и истинным, возведенная в квадрат и усредненная по всему набору данных. Самая простая функция потерь в задаче классификации — точность (процент правильно угаданных меток).

25. Переобучение решающего дерева. Приведите графический пример переобучения модели. Какой результат точности обучения мы получим для переобученной модели на тестовой и валидационной выборке? Критерии останова для решающего дерева.
К оглавлению

Переобучение — это свойство модели очень хорошо предсказывать метки данных, использовавшихся для обучения, но часто допускать ошибки при применении к образцам, которые алгоритм обучения не видел прежде.

Для того, чтобы её избежать, необходимо использовать метод «регулирования глубины дерева». Это техника, которая позволяет уменьшать размер дерева решений, удаляя участки дерева, которые имеют маленький вес. Регулирование глубины дерева должно уменьшить размер обучающей модели дерева без уменьшения точности её прогноза или с помощью перекрестной проверки. Есть много методов регулирования глубины дерева, которые отличаются измерением оптимизации производительности.

Наиболее широко используемая версия алгоритма обучения дерева решений называется C4.5. Она решает проблему переобучения с использованием восходящего метода, известного как «подрезка» (отсечение ветвей). Подрезка заключается в том, чтобы выполнить обратный обход только что созданного дерева и удалить ветви, которые не вносят существенного вклада в уменьшение ошибки, заменив их листовыми узлами.

Графический пример переобучения модели:



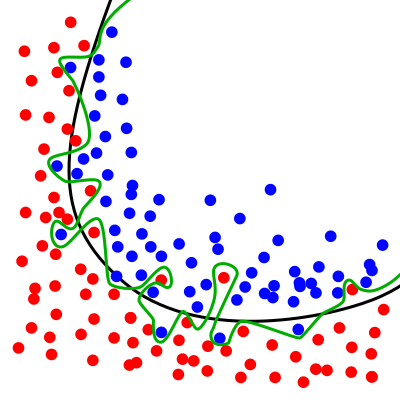
Зелёная разделительная линия показывает переобученную модель, а чёрная линия — регуляризированную модель. Зелёная линия лучше соответствует образцам, по которым проходило обучение, однако классификация по зелёной линии очень зависит от конкретных данных, и скорее всего новые данные будут плохо соответствовать классификации по зелёной линии и лучше — классификации по чёрной линии.

---

Валидационная выборка - используется для контроля процесса обучения. Она поможет предотвратить переобучение и обеспечит более точную настройку гиперпараметров. Тестовый выборка - подмножество данных для оценки производительности модели.

При переобучении модель покажет высокий результат точности на обучающей выборке и результат ниже на тестовой и валидационной выборке.

Критерии останова для решающего дерева:

• 
  Ограничение максимальной глубины дерева.
  
• 
  Ограничение минимального числа объектов в листе.
  
• 
  Ограничение максимального количества листьев в дереве.
  
• 
  Останов в случае, если все объекты в вершине относятся к одному классу
  

26. Алгоритм KNN. Для решения каких задач применяется алгоритм? Формула нахождения Евклидового расстояния. Опишите порядок действий при работе алгоритма. (https://proglib.io/p/metod-k-blizhayshih-sosedey-k-nearest-neighbour-2021-07-19 )
К оглавлению

Метод k-ближайших соседей (k Nearest Neighbors, или kNN) – популярный алгоритм классификации, который используется в разных типах задач машинного обучения.

В случае использования метода для классификации объект присваивается тому классу, который является наиболее распространённым среди k соседей данного элемента, классы которых уже известны.

В случае использования метода для регрессии, объекту присваивается среднее значение по k ближайшим к нему объектам, значения которых уже известны.

На интуитивном уровне суть метода проста: посмотри на соседей вокруг, какие из них преобладают, таковым ты и являешься. Формально основой метода является гипотеза компактности: если метрика расстояния между примерами введена удачно, то схожие примеры гораздо чаще лежат в одном классе, чем в разных.

Помимо простого объяснения, необходимо понимание основных математических составляющих алгоритма k-ближайших соседей.

• 
  Евклидова метрика (евклидово расстояние, или же Euclidean distance) – метрика в евклидовом пространстве, расстояние между двумя точками евклидова пространства, вычисляемое по теореме Пифагора. Проще говоря, это наименьшее возможное расстояние между точками A и B. Хотя евклидово расстояние полезно для малых измерений, оно не работает для больших измерений и для категориальных переменных. Недостатком евклидова расстояния является то, что оно игнорирует сходство между атрибутами. Каждый из них рассматривается как полностью отличный от всех остальных.
  

---

Формула вычисления евклидова расстояния:

• 
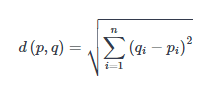
  Другой важной составляющей метода является нормализация. Разные атрибуты обычно обладают разным диапазоном представленных значений в выборке. К примеру, атрибут А представлен в диапазоне от 0.01 до 0.05, а атрибут Б представлен в диапазоне от 500 до 1000). В таком случае значения дистанции могут сильно зависеть от атрибутов с бо́льшими диапазонами. Поэтому данные в большинстве случаев проходят через нормализацию. При кластерном анализе есть два основных способа нормализации данных: MinMax-нормализация и Z-нормализация.
  

Порядок действий при работе алгоритма:

• 
  Загрузите ваши данные.
  
• 
  Инициализируйте k путем выбора оптимального числа соседей.
  
• 
  Для каждого образца в данных:
  

1. Вычислите расстояние между примером запроса и текущим примером из данных.

2. Добавьте индекс образца в упорядоченную коллекцию, как и его расстояние.

• 
  Отсортируйте упорядоченную коллекцию расстояний и индексов от наименьшего до наибольшего, в порядке возрастания.
  
• 
  Выберите первые k записей из отсортированной коллекции.
  
• 
  Возьмите метки выбранных k записей.
  
• 
  Если у вас задача регрессии, верните среднее значение выбранных ранее k меток.
  
• 
  Если у вас задача классификации, верните наиболее часто встречающееся значение выбранных ранее меток k.
  

27. Алгоритм Random Forest. Для решения каких задач применяется алгоритм? Формула итогового классификатора. Порядок действий в алгоритме. Назовите критерии расщепления. Назовите важные параметры для работы алгоритма и объясните их суть.
Благодаря своей гибкости Random Forest применяется для решения практически любых проблем в области машинного обучения. Сюда относятся классификации (RandomForestClassifier) и регрессии (RandomForestRegressor), а также более сложные задачи, вроде отбора признаков, поиска выбросов/аномалий и кластеризации.

Основным полем для применения алгоритма случайного дерева являются первые два пункта, решение других задач строится уже на их основе.

йй

Формула итогового классификатора:



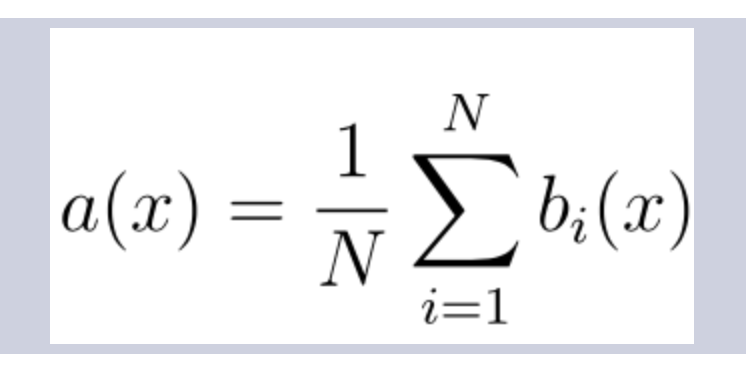
Где

• 
  N – количество деревьев;
  
• 
  i – счетчик для деревьев;
  
• 
  b – решающее дерево;
  
• 
  x – сгенерированная нами на основе данных выборка.
  

---