Файл: 1. Классификация признаков данных (Качественные и количественные, непрерывные и дискретные). Номинальные, порядковые, интервальные, дихотомические, относительные переменные.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 648
Скачиваний: 19
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

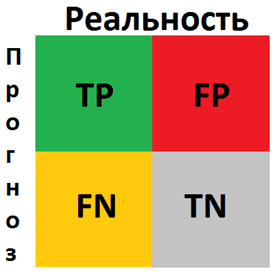 - Матрица ошибок, где TP - верный положительный прогноз, FP - неверный положительный прогноз, FN - неверный отрицательный прогноз, TN - верный отрицательный прогноз.
- Матрица ошибок, где TP - верный положительный прогноз, FP - неверный положительный прогноз, FN - неверный отрицательный прогноз, TN - верный отрицательный прогноз.Точность — это одна из метрик для оценки моделей классификации. Неформально точность — это доля правильных прогнозов, сделанных нашей моделью. Формально точность имеет следующее определение:
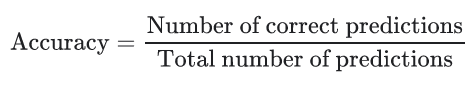
Для бинарной классификации точность также может быть рассчитана с точки зрения положительных и отрицательных результатов следующим образом:
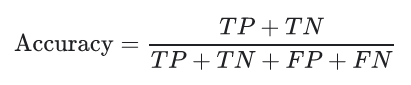
Стоит учесть, что метрика accuracy может быть обманчивой. Один из таких случаев — это несбалансированные данные. Предположим, у нас есть всего 600 единиц данных, из которых 550 относятся к классу Positive и только 50 — к Negative. Поскольку большинство семплов принадлежит к одному классу, accuracy для этого класса будет выше, чем для другого.
Если модель сделала 530 правильных прогнозов из 550 для класса Positive, по сравнению с 5 из 50 для Negative, то общая accuracy равна (530 + 5) / 600 = 0.8917. Это означает, что точность модели составляет 89.17%. Полагаясь на это значение, вы можете подумать, что для любой выборки (независимо от ее класса) модель сделает правильный прогноз в 89.17% случаев. Это неверно, так как для класса Negative модель работает очень плохо.
15. Сформулируйте определения параметрических и непараметрических критериев при тестировании гипотез. Критерий согласия хи-квадрат. Определение и применение.
К оглавлению
Согласно статистическим методам статистические критерии делятся на параметрические и непараметрические.
Параметрические критерии используются в задачах проверки параметрических гипотез и включают в свой расчет показатели распределения, например, средние, дисперсии и т.д. Это такие известные классические критерии, как критерий Стьюдента, критерий Фишера и др. Они позволяют сравнить основные параметры генеральных совокупностей, а также оценить разности средних и различия в дисперсиях. Критерии способны выявить тенденции изменения признака, оценить взаимодействие двух и более факторов в воздействии на изменения признака
Непараметрические критерии проверки гипотез основаны на операциях с другими данными, в частности, частотами, рангами и т.п. Это - критерий Манна-Уитни, критерий Уилкоксона и многие другие. Непараметрические критерии позволяют решить некоторые важные задачи, связанные с выявлением различий исследуемого признака, с оценкой сдвига значений исследуемого признака, выявлением различий в распределениях.
Как параметрические, так и непараметрические методы, используемые для сравнения результатов исследований, т.е. для сравнения выборочных совокупностей, заключаются в применении определенных формул и расчетов определенных показателей в соответствии с предписанными алгоритмами. В конечном результате рассчитывается определенная числовая величина К (эмпирическая), которую сравнивают с табличными пороговыми значениями Ккр (критическими).
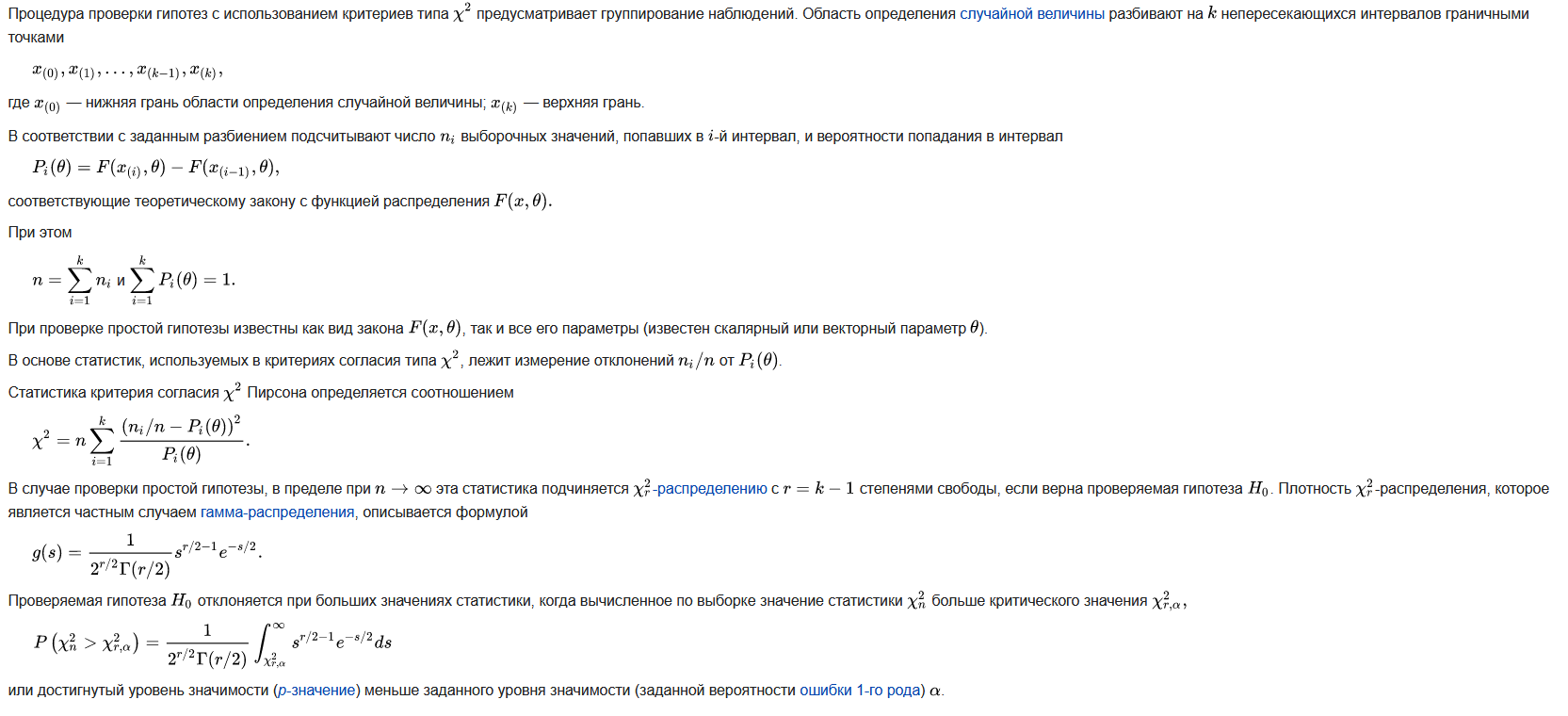
Критерий согласия Пирсона или критерий согласия χ2 (хи-квадрат) — непараметрический метод, который позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы. Выражаясь проще, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей).
Является наиболее часто употребляемым критерием для проверки гипотезы о принадлежности наблюдаемой выборки x1 , x2 , . . . , xn объёмом n некоторому теоретическому закону распределения F ( x , θ ).
Критерий хи-квадрат для анализа таблиц сопряжённости был разработан и предложен в 1900 году основателем математической статистики английским учёным Карлом Пирсоном.
Критерий может использоваться при проверке простых гипотез вида
H 0 : Fn ( x ) = F ( x , θ ) ,
где θ — известный вектор параметров теоретического закона, и при проверке сложных гипотез вида
H0 : Fn ( x ) ∈ { F ( x , θ ) , θ ∈ Θ } ,
когда оценка θ скалярного или векторного параметра распределения F ( x , θ ) вычисляется по той же самой выборке.
16. Критерий независимости хи-квадрат при тестировании гипотез. Для чего используется? Что такие таблица сопряженности?
К оглавлению
Критерий независимости Хи-квадрат используется для определения того, существует ли значительная связь между двумя категориальными переменными.
Критерий независимости Хи-квадрат использует следующие нулевые и альтернативные гипотезы:
H0 : (нулевая гипотеза) Две переменные независимы.
H1 : (альтернативная гипотеза) Две переменные не являются независимыми. (т.е. они связаны)
Мы используем следующую формулу для расчета статистики критерия хи-квадрат X 2 :
Х 2 = Σ(ОЕ) 2 / Е
куда:
Σ: причудливый символ, означающий «сумма».
O: наблюдаемое значение
E: ожидаемое значение
Если p-значение, соответствующее тестовой статистике X 2 со степенями свободы (#rows-1)*(#columns-1), меньше выбранного вами уровня значимости, вы можете отклонить нулевую гипотезу.
Иногда тест независимости Хи-квадрат называют тестом Хи-квадрат на однородность вариаций, но математически они эквивалентны. Идея теста заключается в том, чтобы сравнить информацию выборки (наблюдаемые данные) со значениями, которые можно было бы ожидать, если бы две переменные были действительно независимыми. Основными свойствами теста Хи-квадрат на независимость являются:
-
Распределение статистики теста - это распределение Хи-квадрат, с (r−1)×(c−1) степенями свободы, где r - количество строк, а c - количество столбцов -
Распределение Хи-квадрат является одним из наиболее важных распределений в статистике, наряду с нормальным распределением и F-распределением -
Тест Хи-квадрат на независимость имеет правый хвост
Формула для статистики хи-квадрат имеет вид
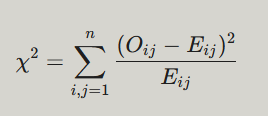
Таблица сопряжённости, или таблица контингентности, факторная таблица в статистике — средство представления совместного распределения двух переменных, предназначенное для исследования связи между ними. Таблица сопряжённости является наиболее универсальным средством изучения статистических связей, так как в ней могут быть представлены переменные с любым уровнем измерения. Таблицы сопряжённости часто используются для проверки гипотезы о наличии связи между двумя признаками с использованием точного теста Фишера или критерия согласия Пирсона.
Строки таблицы сопряжённости соответствуют значениям одной переменной, столбцы — значениям другой переменной, при этом количественные шкалы предварительно должны быть сгруппированы в интервалы. Например, таблица сопряжённости может быть использована для показа зависимости музыкальных предпочтений от места проживания слушателей.
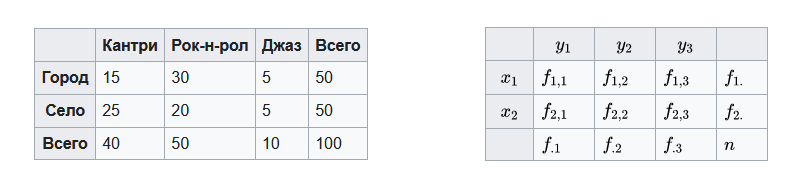
На пересечении строки и столбца указывается частота совместного появления fij соответствующих значений двух признаков xi и yj. Сумма частот по строке fi. называется маргинальной частотой строки; сумма частот по столбцу f.j — маргинальной частотой столбца. Сумма маргинальных частот равна объёму выборки n; их распределение представляет собой одномерное распределение переменной, образующей строки или столбцы таблицы. В таблице сопряжённости могут быть представлены как абсолютные, так и относительные частоты (в долях или процентах). Относительные частоты могут рассчитываться по отношению: а) к маргинальной частоте по строке; б) к маргинальной частоте по столбцу; в) к объёму выборки.
17. Параметрические критерии. t-статистика. Напишите определение и формулу для вычисления. Понятие степеней свободы.
Параметрическими называют критерии, которые основаны на предположении, что распределение признака в совокупности подчиняется некоторому известному закону. К таким критериям относятся критерии Стьюдента, Фишера, Пирсона и т.д.
К оглавлению
t-статистика - это параметрический критерий, который измеряет, насколько значительна разница между двумя выборочными средними по отношению к изменчивости данных (используется для проверки гипотез о среднем значении генеральной совокупности при неизвестной дисперсии). Это стандартный инструмент для оценки гипотез о значимости различий между выборками.
Формула для вычисления t-статистики:
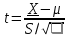
где X - выборочное среднее
μ - гипотетическое среднее
S - выборочное стандартное отклонение
n - размер выборки.
Степени свободы - это число независимых наблюдений в выборке, которые могут свободно изменяться (и говорят вам, сколько элементов может быть выбрано случайным образом, прежде чем должны быть введены ограничения). В t-статистике степени свободы равны n - 1, где n - размер выборки. Они используются для определения критического значения t-статистики и расчета p-значения.
Пример определения степеней свободы:
Рассмотрим выборку данных, состоящую из пяти натуральных чисел. Значения пяти целых чисел должны иметь среднее значение шесть. Если четыре элемента в наборе данных равны {3, 8, 5, 4}, пятое число должно быть 10. Поскольку первые четыре числа могут быть выбраны случайным образом, степень свободы равна четырем.
18. Одновыборочный и парный t-тест. Объяснить разницу. Придумать пример на тестирование гипотезы одним из тестов, вычислить t-наблюдаемое.
К оглавлению
Одновыборочный t-тест используется для проверки гипотезы о среднем значении генеральной совокупности, когда известна ее дисперсия. Парный t-тест используется для сравнения двух средних значений, полученных из двух связанных выборок.
Чтобы было понятнее: