Файл: 1. Классификация признаков данных (Качественные и количественные, непрерывные и дискретные). Номинальные, порядковые, интервальные, дихотомические, относительные переменные.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 631
Скачиваний: 19
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
10. Определение корреляции в данных. Свойства коэффициента корреляции. Формула для нахождения коэффициента корреляции.
К оглавлению
Представим, что у нас есть данные о росте и весе нескольких собак. Нарисуем систему координат, где по оси абсцисс будет рост, а по оси ординат — вес. И расположим точки так, чтобы каждая точка соответствовала одной собаке, а координаты этой точки соответствовали росту и весу этой собаки:
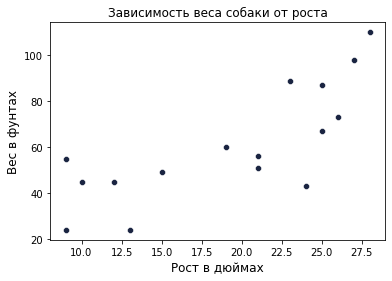
Мы можем видеть, что есть определенная закономерность в том, как располагаются данные точки. Очевидно, что есть тенденция к тому, что рост и вес собаки увеличиваются совместно, что между ними есть линейная взаимосвязь. В математической статистике такую взаимосвязь называют корреляцией. Важно отметить, что взаимосвязь может быть разной. Например, на данных рисунках можно видеть линейную, квадратичную и кубическую взаимосвязи:

Однако в ходе корреляционного анализа мы можем выявить только линейную взаимосвязь. И далее, когда мы будем говорить о корреляции и о взаимосвязи двух величин, мы будем иметь в виду именно линейную взаимосвязь.
Корреляция — это мера линейной взаимосвязи между двумя величинами.
То есть, если два признака линейно взаимосвязаны, то мы говорим, что они коррелируют. Например, чем больше студент посещает лекции — тем выше у него будет оценка за дисциплину. Значит, признак «посещаемость лекций» будет коррелировать с признаков «оценка за дисциплину». Сила корреляции (взаимосвязи) выражается числом, которое называется коэффициентом корреляции.
Свойства коэффициента корреляции
1. Изменяется от −1 до 1
Причем чем ближе коэффициент корреляции по модулю к 1, тем сильнее связь. То есть, например, если коэффициент корреляции 0.89 или 0.92 — это сильная связь. А если коэффициент 0.14 или −0.03 — это слабая связь.
Нет четких границ, которые определяют, при каких значениях слабая связь становится средней, а средняя — сильной. Ориентировочно можно делать выводы согласно классификации, которую предложил математик Чеддок: слабая — от 0.1 до 0.3; умеренная — от 0.3 до 0.5; заметная — от 0.5 до 0.7; высокая — от 0.7 до 0.9; весьма высокая (сильная) — от 0.9 до1.0 .
Визуально можно примерно определить, сильная или слабая связь по тому, насколько точки на диаграмме рассеяния стремятся выстроиться в одну линию. Ниже можно видеть примеры диаграмм для различных коэффициентов корреляций. При отсутствии корреляции точки представляют собой просто неупорядоченное хаотичное множество, при более сильной уже видна тенденция на линейную взаимосвязь, а при сильной — уже выстраивается практически четкая линия из точек.
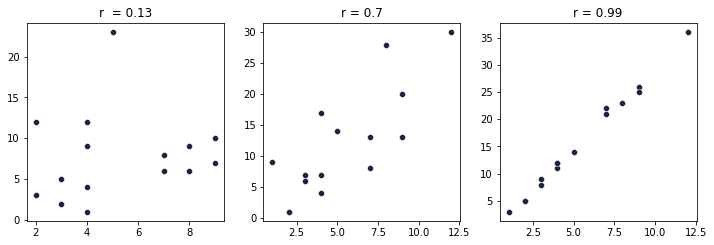
2. Положительный коэффициент корреляции свидетельствует о прямой зависимости.
Например, прямая зависимость может быть между знаниями по математике и по информатике (так как обычно для освоения технических наук нужны схожие знания и способности). То есть, когда значение одного признака увеличивается, то значение другого тоже увеличивается.
Если визуализировать такую взаимосвязь на точечной диаграмме, то она будет выглядеть следующим образом:
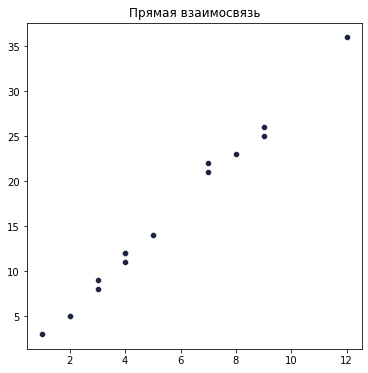
3. Отрицательный коэффициент корреляции свидетельствует об обратной зависимости.
Например, обратную зависимость можно наблюдать между количеством работы и количеством сна. Чем больше количество работы — тем меньше количество сна. И чем больше количество сна — тем меньше количество работы. То есть, когда значение одного признака увеличивается, то значение другого уменьшается. Ниже можно видеть пример визуального отображения такой взаимосвязи на диаграмме:
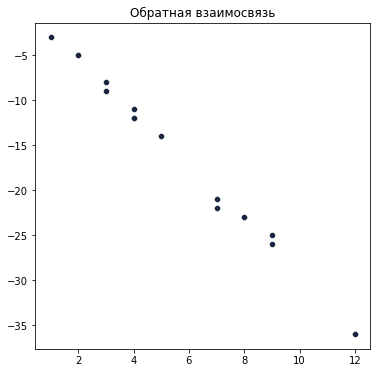
Для того чтобы оценить силу и направление линейной взаимосвязи, мы будем рассчитывать коэффициент корреляции Пирсона (обычно его обозначают маленькой буквой r) по следующей формуле:
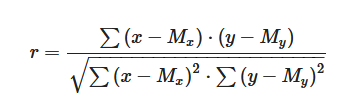
Рассмотрим по шагам, как вычислить коэффициент корреляции.
Пусть у нас есть две переменные Х и У, для которых мы хотим вычислить коэффициент корреляции:
X | Y |
| 2 | 6 |
| 4 | 8 |
| 1 | 1 |
| 3 | 7 |
| 5 | 3 |
Вычислим среднее значение для переменной X:
2+4+1+3+55=3
Теперь из каждого значения X вычтем среднее значение и возведем полученную разность в квадрат:
| X | X−Mx | (X−Mx)2 |
| 2 | 2 - 3 = -1 | 1 |
| 4 | 4 - 3 = 1 | 1 |
| 1 | 1 - 3 = -2 | 4 |
| 3 | 3 - 3 =0 | 0 |
| 5 | 5 - 3 =2 | 4 |
Сумма разностей значений X и средних в квадрате равна:
1+1+4+0+4=10
Теперь вычислим среднее значение для переменной Y:
6+8+1+7+35=5
Теперь из каждого значения Y вычтем среднее значение и возведем полученную разность в квадрат:
| Y | Y−MY | (Y−MY)2 |
| 6 | 6 - 5 = 1 | 1 |
| 8 | 8 - 5 = 3 | 9 |
| 1 | 1 - 5 = -4 | 16 |
| 7 | 7 - 5 = 2 | 4 |
| 3 | 3 - 5 = -2 | 4 |
Сумма разниц в квадрате равна:
1+9+16+4+4=31
Перемножим значения двух столбцов с разницами:
| X−Mx | Y−MY | (X−Mx)⋅(Y−My) |
| -1 | 1 | -1 |
| 1 | 3 | 3 |
| -2 | -4 | 8 |
| 0 | 2 | 0 |
| 2 | -2 | -4 |
Теперь сложим все произведения:
−1+3+8+0–4=6
Вычисляем коэффициент корреляции. В числителе у нас будет сумма произведений, которую мы посчитали в строке выше (то есть, 6). А в знаменателе будет корень из произведения суммы квадратов ( 10 и 31). То есть, корень из 310. Получаем:
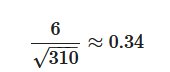
Итак, мы вычислили, что коэффициент корреляции между двумя признаками равен примерно 0.34, если округлять до сотых. То есть, между этими двумя признаками есть умеренная положительная связь.
При корреляционном анализе мы оцениваем общую тенденцию, поэтому при изменениях одной из переменной, которые не влияют на общий паттерн, коэффициент корреляции не будет меняться.
Например, подумаем о взаимосвязи количества часов подготовки и оценки за экзамен. Представим, что у нас есть данные о некотором количестве студентов: их оценка, и время, потраченное на изучение материала. И визуально эту взаимосвязь мы можем отобразить следующим образом:
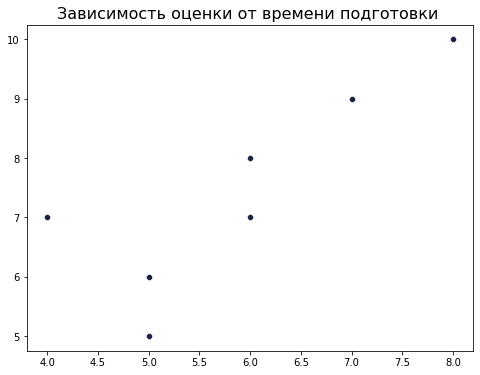
Если мы увеличим каждую оценку на 2, то диаграмма изменится следующим образом:
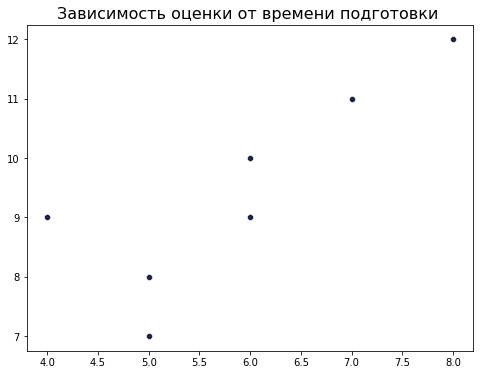
Можно заметить, что общий паттерн взаимосвязи остался ровно такой же, какой был ранее, просто все точки сместились на 2 по оси ординат.
Теперь попробуем домножить время для каждого студента на 2 и посмотрим на изменившуюся диаграмму:
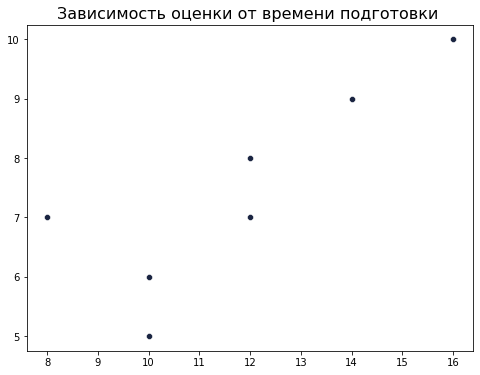 я
яИзображение точек растянулось по горизонтали в 2 раза, но форма взаимосвязи осталась такой же.
Итак, домножение переменной на положительную константу или прибавление константы никак не меняет коэффициент корреляции и силу связи. В случае домножения на отрицательную константу коэффициент корреляции меняет знак, но сила взаимосвязи остается прежней.
Необходимость домножения переменной может возникнуть, например, когда мы переводим одни единицы измерения в другие: часы в минуты, доллары в рубли, килограммы в граммы и т.д.
Использование и интерпретация корреляции
Важно понимать, что корреляция свидетельствует именно о взаимосвязи, но ни в коем случае нельзя делать на основе корреляционного анализа выводы о причинно-следственных связях. Если между признаками А и Б есть тесная взаимосвязь, то мы не может говорить, что А влияет на Б или Б влияет на А.
Рассмотрим эту мысль на примере. Допустим, мы ведем статистику по пожарам. У нас есть данные об ущербе и о количестве пожарных, которые тушили пожар. Скорее всего, между этими двумя признаками есть тесная взаимосвязь: при маленьком ущербе мало пожарных и при большом ущербе — много пожарных. Но из этого не следует наличие причинно-следственных связей. Будет странным говорить, что пожарные приводят к убыткам. Такая взаимосвязь может наблюдаться из-за того, что на оба признака влияет третий — масштаб пожара. При серьезной ситуации будут большие потери, и на место тушения вызовут много бригад. Если же ситуация не критическая, то ущерб будет минимальный, и пожарных тоже будет мало. То есть, две величины меняются пропорционально, но совсем не из-за того, что одна из них влияет на другую.
Теперь обсудим, как применяется корреляционный анализ в исследованиях и практических задачах.
Во-первых, мы можем использовать его для прогнозирования. Если мы знаем, что две переменные связаны определенным образом, то мы можем прогнозировать значение одной по значению другой. Например, мы выяснили, что оценки за ЕГЭ по математике и информатике сильно коррелируют. Тогда мы можем предполагать, что если у школьника хороший балл по математике, то и по информатике он тоже будет высокий. Но такой прогноз будет не совсем точен. Не у всех, кто получил высокий балл по математике, будет высокий балл по информатике. И не у всех, кто получил низкий балл по математике, будет низкий балл по информатике. Более корректные предсказания можно делать на основании регрессионных моделей.
Во-вторых, корреляцию можно использовать для оценки валидности разных тестов. Например, если психолог разработал тест для определения уровня тревоги, то его результаты должны показывать сильную корреляцию с другими показателями, которые точно идентифицируют тревожность (например, физиологические индикаторы).
В-третьих, с помощью корреляции вычисляется надежность оценочных инструментов. Предположим, некий студент сдает экзамен, чтобы получить сертификат по английскому языку. Если он сдает его два раза через небольшие промежутки времени, то его результаты должны быть практически одинаковые, если экзамен действительно хорошо составлен и условия проведения не изменились. Поэтому для оценки надежности теста можно провести его на группе людей, а потом повторить процедуру. Если корреляция между результатами сильная, то можно говорить о надежности инструмента.