Файл: 1. Классификация признаков данных (Качественные и количественные, непрерывные и дискретные). Номинальные, порядковые, интервальные, дихотомические, относительные переменные.docx

6. Меры центральной тенденции. Перечислить основные типы, написать формулу для нахождения. Какие меры вариативности подвержены выбросам в данных? Подтвердите выводы на примере.

Ты никогда не выйдешь из моды, если ты — мода: что измеряют меры центральной тенденции

К оглавлению

Для начала мы визуально отобразим все значения изученных нами показателей на гистограмме частот, где по оси Х будут откладываться полученные значения, а по оси Y количество этих значений.

Например, мы изучали какой рост встречается в определенной группе людей. По оси Х мы отразим все полученные нами переменные, а по оси Y – сколько людей имели тот или иной рост (это может быть отражено как столбцами, так и просто линией).



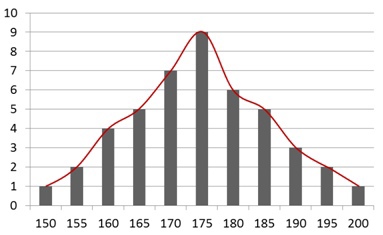
Изобразив график, мы можем начать изучение полученного нами распределения показателей. Этим занимается описательная статистика. Она включает два больших раздела. Нас может интересовать как что-то единое, общее для всех известных нам переменных (меры центральной тенденции), проще говоря — поможет ответить на вопрос, что объединяет наши данные, так и то, насколько эти переменные друг от друга отличаются (меры изменчивости).

Мода, медиана, среднее значение

Итак, меры центральной тенденции включают в себя множество понятий. Некоторые мы уже упоминали, о некоторых будем говорить в других статьях. Сегодня же мы опишем самые базовые.

К ним относятся:

• Мода

• Медиана

• Среднее значение

Мода

Это понятие кажется нам интуитивно понятным благодаря далеко не медицинским знаниям и, грубо говоря, оно обозначает именно то, что мы все представляем, слыша это слово. Мода – это самое частое встречающееся значение в описываемой совокупности.

На графике моду обозначает самая высокая точка пика. Если два соседних значения встречаются одинаково часто и чаще, чем любое другое значение, мода есть среднее этих двух значений. Так описывается унимодальное распределение.

---

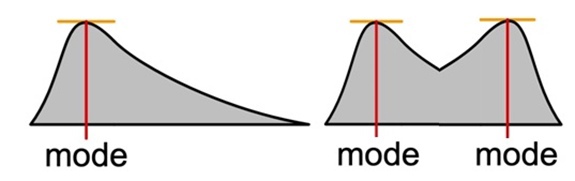
Примеры мод в унимодальном (слева) и бимодальных распределениях (справа)

Не стоит забывать, что мода не обязательно бывает одна. Моды может не быть вовсе, когда все значения встречаются одинаково часто. Либо мод может быть две и более. Такое распределение называется бимодальным или полимодальным соответственно.

В конце еще раз отметим, что мода — это значение признака, а не его частота. Например, модой на имена среди авторов данной статьи является имя Александр, а не цифра 2

Медиана

Это понятие тоже известно нам всем еще со школы. Что-то из геометрии. Вспоминаете? Так же как там, в статистике она делит значения на прямой ровно пополам. То есть слева и справа от медианы будут отложены одинаковое количество значений. При этом не важно, есть ли выбросы и симметрично ли распределение.

Выброс — экстремально малое или большое значение переменной, выбивающееся из общей картины.

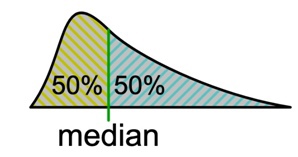
Среднее значение

Опять все просто и все всё понимают. Ну не тема, а сплошное удовольствие. Среднее – это результат деления суммы всех значений на количество этих значений. Тут уже очень важна симметричность и выбросы, потому что, как все знают, средняя температура и зарплата по больнице всегда очень неплохие.



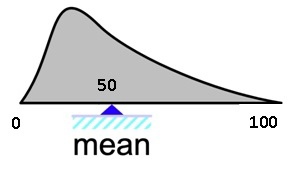
На величину среднего влияет каждое отдельное значение, а также количество всех полученных значений. Поэтому среднее весьма чувствительно к выбросам и нивелировать их способна только огромная выборка, что может быть накладно. Главное преимущество медианы в ее устойчивости к выбросам — аномально большим или малым значениям, так как при их появлении будет учитываться не значение признака, а лишь количество этих значений.

• 
  К мерам центральной тенденции относятся: мода, медиана, и среднее значение.
  
• 
  Мода – это самое частое встречающееся значение в описываемой совокупности. Чаще всего мода используется при описании номинативных переменных.
  
• 
  Медиана — это такое число, при значении которого половина из элементов выборки больше него, а другая половина меньше. Используется в медицинской статистике чаще всего, так как устойчива к выбросам и не так требовательна к размерам выборки, как среднее.
  
• 
  Среднее – это результат деления суммы всех значений на количество этих значений. Чувствительно к выбросам, и потому используется тогда, когда учет этих выбросов важен.
  

---

7. Стандартизированное распределение (z-распределение) и его свойства. Для чего используется? Напишите формулу для нахождения z-оценки. Придумайте пример для нахождения стандартизированного распределения, визуализируйте полученный результат
К оглавлению

Давайте представим такую ситуацию: вы написали тест по статистике и получили за него 76 баллов из 100 Насколько это результат хорош относительно других слушателей курса? Это может быть, как лучший результат, так и одна из самых низких оценок. Предположим, что мы знаем, что средняя оценка за этот тест — 70 баллов. Отлично! Значит вы справились лучше среднего. Но мы уже говорили, что, описывая распределение только с помощью меры центральной тенденции, можно угодить в ловушку. Если среднеквадратичное отклонение нашего распределения равно 3 (σ=3), то большинство оценок находится в диапазоне 67–73 балла. И результат в 76 баллов в этом контексте будет среди лучших оценок. Однако если оценка пришла из другого распределения, скажем, со среднеквадратичным отклонением 12 (σ=12), то это значит, что большинство сдававших набрали от 58 до 82 баллов. И вы среди этого большинства. Таким образом, относительная позиция значения в распределении действительно зависит и от среднего, и от среднеквадратичного отклонения. А значение переменной само по себе не несет много информации. В прошлых главах мы говорили о среднем арифметическом и среднеквадратичном отклонении в контексте описания распределений наших переменных. А теперь мы попробуем использовать эти понятия для того, чтобы описать отдельные значения с помощью z-оценок. Это способ выразить любое значение переменной в количестве среднеквадратичных отклонений от среднего распределения. С помощью z-оценок мы можем стандартизировать распределение — выразить все значения в терминах дистанции от среднего. Поэтому z-оценка еще называется стандартизированной. Стандартизированная оценка (z-оценка) — это относительная мера, которая показывает, на сколько среднеквадратичных отклонений наблюдаемое значение отличается от среднего значения распределения. Знак z-оценки показывает, находится ли значение левее среднего (–) или правее среднего (+).

Выразим z-оценку формулой для генеральной совокупности:



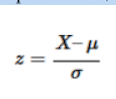
И для выборки:



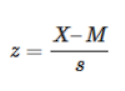
В числителе у нас находится отклонение значения от среднего. А разделив его на среднеквадратичное отклонение, мы как раз находим расстояние от значения до среднего в единицах среднеквадратичных отклонений.

---

Можно еще услышать, когда говорят, что значение находится на расстоянии «сколько-то сигм» от среднего. Кстати, зная z-оценку, среднее и среднеквадратичное отклонение, можно легко восстановить и оригинальное значение. Для генеральной совокупности:



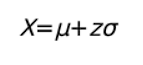
Для выборки:



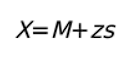
Давайте попробуем рассчитать z-оценку для X=95, принадлежащего генеральной совокупности с μ=86 и σ=7

z=(X–μ)/σ=(95−86)/7=9/7=1.29

Таким образом, мы можем сказать, что наблюдение X=95 находится на расстоянии 1.29 среднеквадратичного отклонения выше среднего.

А теперь давайте по оценке найдем оригинальное значение. Мы знаем, что z=–1.50, μ=60 и σ=8. Восстанавливаем значение по формуле:

X=μ+zσ=60+(–1.50∗8)=60–12=48

Если мы превратим все значения переменной в распределении в z-оценки, то мы получим z-распеределение или стандартизированное распределение. Такое распределение сохранит форму оригинального распределения, но среднее в нем будет равно нулю, а среднеквадратичное отклонение — единице.

Представьте, что нам нужно сравнить результаты тестирования двух групп студентов, которые сдавали разные экзамены по английскому языку. Первая группа писала тест, оцениваемый по шкале от 0 до 9, а вторая — от 0 до 120 С теми студентами, которые набрали максимальное количество баллов или наоборот умудрились получить 0 — все просто. Их оценки мы можем сравнить друг с другом. А дальше начинаются вопросы — лучше ли оценка 60 из 120 чем 5 из 9? Тут нам и помогут стандартизированные распределения. После того как мы найдем z-оценку для каждого оригинального значения переменной в двух группах, мы сможем сравнить оценки между собой.

Z-распределение обладает и важными свойствами. Через z-оценки мы можем описать пропорции нормального распределения:

Если в случае с интерквартильным размахом мы знаем, что он дает нам информацию о разбросе в центральных 50% выборки, то теперь мы можем оценивать и количество данных в частях нормального распределения. Так в интервале от минус одного до плюс одного среднеквадратичного отклонения располагается примерно 68% выборки — то есть самые типичные для нее значения. Знание этих пропорций пригодится и при разговоре о тестировании гипотез, когда мы будем оценивать вероятность случайного получения некоторых значений.

---

---