Файл: 1. Классификация признаков данных (Качественные и количественные, непрерывные и дискретные). Номинальные, порядковые, интервальные, дихотомические, относительные переменные.docx

К оглавлению

А раз мы работаем с выборками, а выводы будем делать о генеральной

совокупности, то наши выводы будут носить некоторый вероятностный характер.

Ведь мы знаем, что наша выборка не может на 100% соответствовать генеральной совокупности, из которой она взята. Больше всего проблем с маленькими выборками.

Например, мы хотим узнать, какой объем кофе в среднем выпивают студенты нашего университета в неделю.
Распределение выборочных средних выборок заданного размера всегда будет стремиться к форме нормального распределения, а его среднее будет равно среднему генеральной совокупности. Среднеквадратичное отклонение такого распределения будет равно среднеквадратичному отклонению генеральной совокупности, разделенного на

квадратный корень из размера выборки. Среднее распределения выборочных средних называется математическим ожиданием выборочного среднего, а его среднеквадратичное отклонение — стандартной ошибкой выборочного среднего (SEM — Standard Error of Mean или σM)

Эти свойства описываются центральной предельной теоремой (ЦПТ).
Центральная предельная теорема: для любой генеральной совокупности со средним μ и среднеквадратичным отклонением σ распределение выборочных средних выборок размера n будет иметь среднее μ и среднеквадратичное отклонение σn√, а его форма будет стремиться к нормальной при n стремящемся к бесконечности.

Соответственно, здесь будет работать закон больших чисел (ЗБЧ) — чем больше размер выборки, тем больше вероятность, что значение его среднего будет близко к среднему генеральной совокупности.
12. Разделение выборки на обучающую и валидационную. Какое отношение данных обучающей выборки к валидационной обычно используется, для чего используются выборки? Опишите процесс стратификации данных, объясните для чего он используется.
К оглавлению

при построении предсказательных моделей исходные данные обычно разбиваются на обучающую ("training set") и контрольную ("test set", "validation set") выборки. Обучающая выборка используется собственно для "обучения" той или иной модели, т.е. для построения математических отношений между некоторой переменной-откликом и предикторами, тогда как

контрольная (= "проверочная", "экзаменационная") выборка служит для получения оценки прогнозных свойств модели на новых данных, т.е. данных, которые не были использованы для обучения модели. Как правило, обучающая выборка составляет 75-80% от объема исходных данных, хотя каких-то строгих правил в этом отношении не существует.
Стратификация — метод выбора подмножества объектов из генеральной совокупности, разбитой на подмножества (страты). При стратификации объекты выбираются таким образом, чтобы итоговая выборка сохраняла соотношения размеров страт (либо контролируемо нарушала эти соотношения, см. пункт 3). Скажем, в рассмотренном примере генеральная совокупность — точки внутри единичного квадрата; стратами являются наборы точек внутри квадратов меньшего размера.
13. Постановка и тестирование гипотез. Что такое нулевая и альтернативная гипотеза? Виды альтернативных гипотез. Что такое уровень статистической значимости α? Определение критической области. Ошибка первого и второго рода.
Проверка статистических гипотез – это пятиступенчатая процедура, которая на основании данных выборки и при помощи теории вероятностей позволяет сделать вывод об обоснованности гипотезы.

Другими словами, этот способ проверить, действительны ли результаты, полученные на выборке, и для генеральной совокупности.

Пошаговый алгоритм:

1.Формулировка основной и альтернативной гипотезы

2.Выбор уровня значимости

3.Определение подходящего статистического критерия

4.Формулировка правила принятия решения

5.Принятие решения на основании данных выборки

Шаг 1: Формулировка основной и альтернативной гипотезы

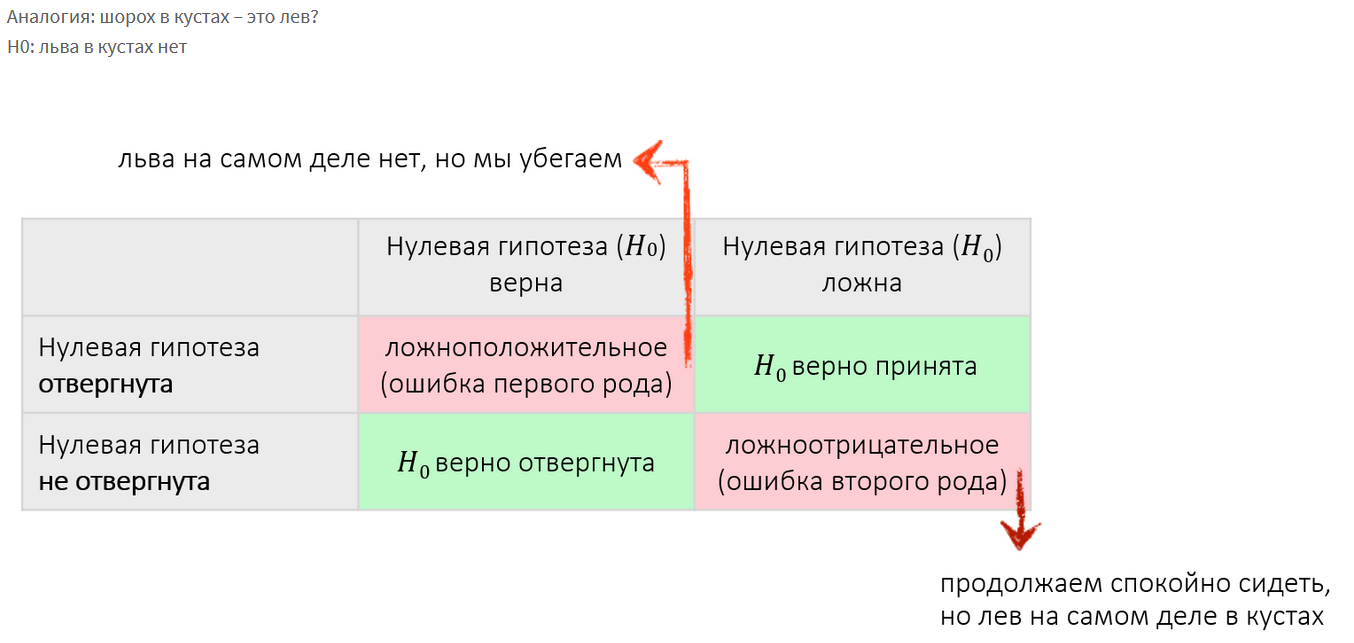
Нулевая гипотеза (H0) – это утверждение статус-кво, что никакой разницы или никакого эффекта на самом деле нет.

Альтернативная гипотеза (H1) утверждает, что некоторая разница (или эффект) все таки должна быть. Бывает направленная и ненаправленная.

H0: в отношении частоты пользования интернетом разницы между мужчинами и женщинами нет.

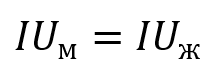
H1: мужчины и женщины пользуются интернетом с разной частотой.

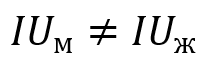
Шаг 2: Выбор уровня значимости

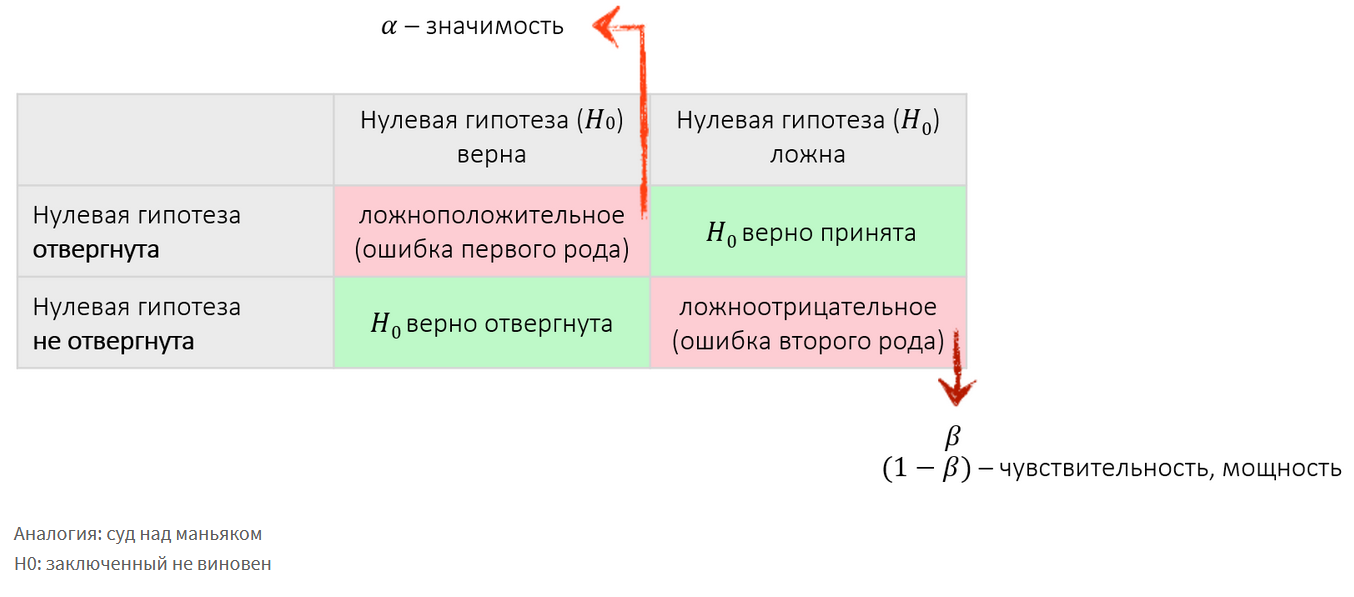
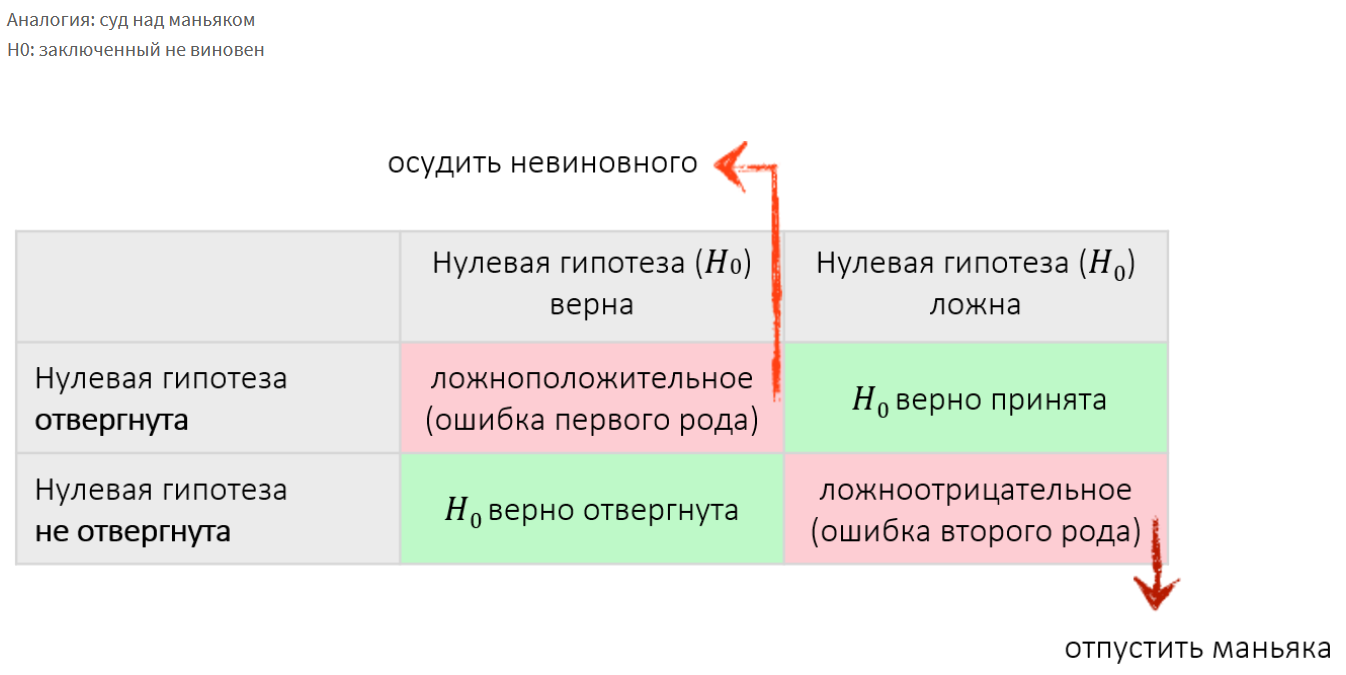
Значимость (α) – вероятность того, что верная нулевая гипотеза будет отвергнута.

β – вероятность того, что ложная нулевая гипотеза будет принята.

Уровни значимости, принятые в маркетинговых исследованиях:

α – уровень значимости

0,01 (1%)

0,05 (5%)

(1-α) – уровень доверия (доверительная вероятность)

0,99 (99%)

0,95 (95%)

Шаг 3: Определение статистического критерия

Критерий χ2 (хи-квадрат) используется для проверки статистической значимости взаимосвязей между переменными, наблюдаемых в перекрестных таблицах.

H0: взаимосвязи между переменными нет

Тест χ2 проверяет равенство частотных распределений.
Какие распределения/частоты мы должны проверить?

fо – ожидаемые частоты (расчётные значения), которые бы стояли в ячейках, в случае когда связи между переменными нет.

fн – реально наблюдаемые частоты, т.е. значения, которые стоят в составленной нами таблице

Расчёт χ2 следует производить только на основе абсолютных значений частот. Если исходные данные представлены в процентах, то их необходимо пересчитать а абсолютные частоты.

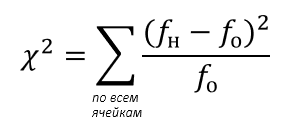
В нашем примере:

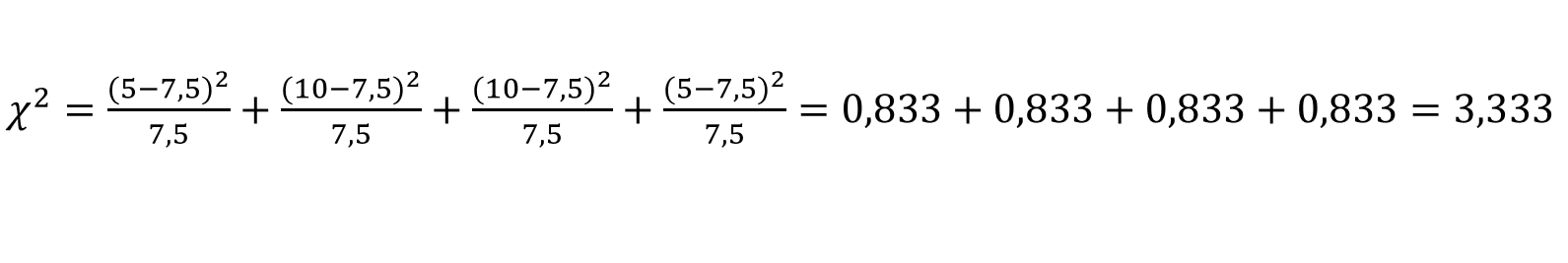
Шаг 4: Формулировка правила принятия решения

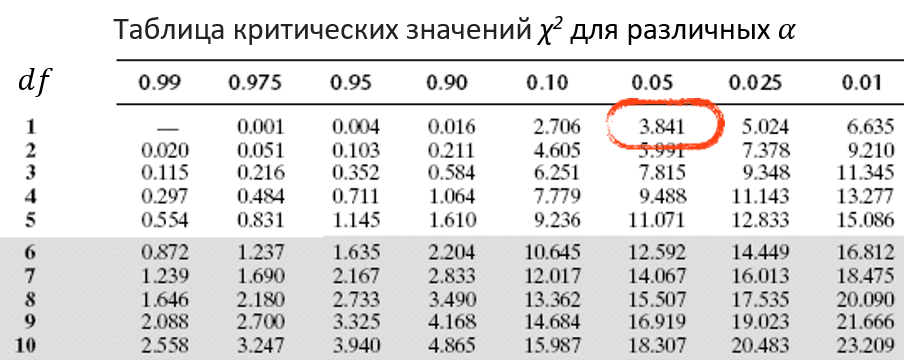
Kн – наблюдаемое (расчётное) значение статистического критерия.

Kкрит– критическое значение статистического критерия для заданного уровня значимости.

Если вероятность Кн меньше уровня значимости (α), то H0 надо отклонить.

или

Если Kн>Kкрит , то H0 надо отклонить.

Таблица критических значений χ2 для различных α

df=(r-1)(c-1)

df – количество степеней свободы
r – количество строк
c – количество столбцов

df=(2-1)(2-1)=1

H0 не может быть отклонена

Шаг 5: Принятие решения

Нашлись ли доказательства? Что из этого следует?

- H0 отсутствия различий не может быть отклонена

- Различия не являются статистически значимыми на уровне 0,05

- Полученные на выборке результаты не могут быть обобщены на генеральную совокупность

Пол и частота пользования интернетом

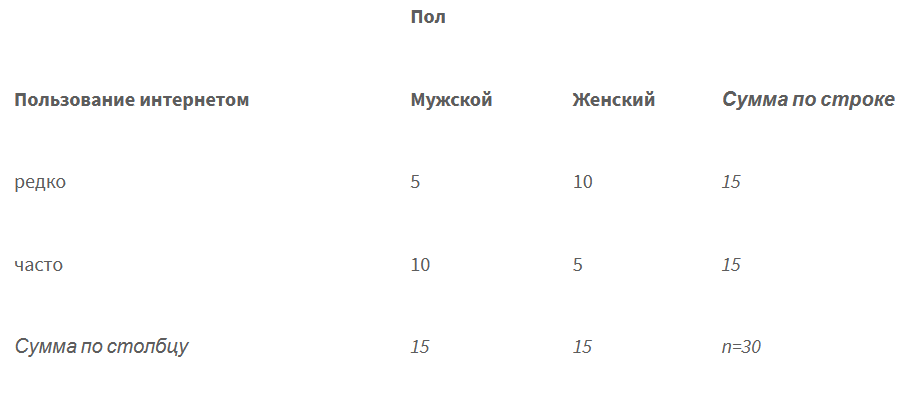
Вопрос:

Можем ли мы на основании этой выборки утверждать, что во всем населении среди мужчин больше активных интернет пользователей, чем среди женщин?

Ответ:

Данная выборка не дает оснований для таких утверждений.
Если выборка была произведена должным образом, то мы можем с 95% доверительной вероятностью констатировать, что взаимосвязи между полом и частотой пользования интернетом нет. В противном случае – мы не знаем ответа.

Альтернативная гипотеза, альтернатива

Предположение, принимаемое в случае отклонения нулевой гипотезы (H₀). Как правило, альтернативная гипотеза (H₁) — это единственное утверждение, являющееся логическим отрицанием нулевой гипотезы. Часто альтернативная гипотеза означает наличие связи между изучаемыми переменными.

Пример:

Нулевая гипотеза (H₀): связи между признаками нет,

Альтернатива (H₁): связь между признаками есть.

двусторонняя альтернатива:

односторонняя альтернатива:

или

Альфа-уровень

-уровень - пороговый уровень статистической значимости; вероятность ошибочно отклонить нулевую гипотезу.

Чем меньше

-уровень, тем меньше риск совершения этой ошибки. Устанавливается исследователем произвольно (обычно принимается равным 0,05, 0,01 или 0,001).

Критическая область проверки гипотезы

Область выборочного пространства; при попадании статистики критерия в критическую область, нулевая гипотеза отклоняется.

Обычно критическая область выбирается так, чтобы попадание в неё статистики критерия имело:

а) низкую вероятность, когда нет оснований для отклонения нулевой гипотезы

б) высокую вероятность, когда нулевая гипотеза отклоняется

Назначение уровня значимости, равного

, означает вероятность попадания статистики критерия в критическую область при верной нулевой гипотезе.

Ошибка I рода

Вероятность неверного отклонения нулевой гипотезы, т. е. отклонения нулевой гипотезы, когда она на самом деле верна («ложная тревога»).

Синоним:

-error.

Ошибка II рода

Вероятность остаться в рамках нулевой гипотезы, когда на самом деле она не верна («пропуск цели»).

Синоним:

-error.
14. Метрики качества моделей машинного обучения. Изобразите матрицу ошибок для бинарной классификации. Напишите формулу для вычисления True Positive Rate и False Negative Rate. Метрика Accuracy. В каких случаях её применение даёт ложный результат о качестве модели? Что такое ROC-кривая. Что такое AUC ROC.
К оглавлению

Кривая ROC (кривая рабочих характеристик приемника ) представляет собой график, показывающий эффективность модели классификации при всех пороговых значениях классификации. Эта кривая отображает два параметра: истинная положительная скорость, ложноположительный результат.

AUC означает «Площадь под кривой ROC». То есть AUC измеряет всю двумерную область под всей кривой ROC (например, интегральное исчисление) от (0,0) до (1,1) .AUC обеспечивает совокупный показатель производительности по всем возможным пороговым значениям классификации. Один из способов интерпретации AUC — это вероятность того, что модель ранжирует случайный положительный пример выше, чем случайный отрицательный пример.