Файл: 1. Классификация признаков данных (Качественные и количественные, непрерывные и дискретные). Номинальные, порядковые, интервальные, дихотомические, относительные переменные.docx

Одновыборочный - При выполнении этого теста среднее или среднее значение одной группы сравнивается с установленным средним значением, которое является либо теоретическим значением, либо средним значением для населения. Например, учитель хочет определить средний рост учеников 5-го класса и сравнить его с установленным значением более 45 кг.

Парный - Эта проверка гипотезы проводится, когда две группы принадлежат к одной и той же популяции или группе. Группы изучаются либо в два разных времени, либо в двух различных условиях.
Пример для одновыборочного t-теста: предположим, что средний вес яблок в магазине должен быть не менее 150 граммов. Взяв выборку из 20 яблок, мы получили средний вес 145 граммов и выборочное стандартное отклонение 10 граммов. Вычисляем t-наблюдаемое: t = (145 - 150) / (10 / √20) = -2.24. Если уровень значимости α = 0.05 (типичное значение по условие) и степени свободы 19 (20-1), то критическое значение t-статистики (табличка сделанная математиками, где значения, определяемые по уровню значимости и степеням свободы) равно ±2.093. Так как t-наблюдаемое меньше критического значения, мы отвергаем гипотезу о среднем весе яблок в магазине не менее 150 граммов.

Уровень значимости статистического теста – это вероятность отклонить нулевую гипотезу, когда на самом деле она верна. о


19. Линейная регрессия. Нахождение уравнения регрессии. Напишите формулу для поиска коэффициентов линейного уравнения. Приведите практический пример и постройте график уравнения регрессии по собственным данным.
К оглавлению

Линейная регрессия - это метод машинного обучения, который используется для построения модели, которая описывает линейную зависимость между входными признаками и выходными значениями.



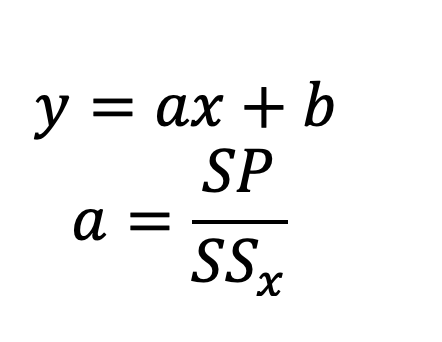
Где

SP- сумма произведений отклонений

SS_x-сумма квадратов отклонений



Давайте накинем примерчик

Под X и Y подставляем любые рандомные слова (из примера скомуниздим площадь и стоимость, мои

---

цифры будут совершенно не похоже, но пофикккк)

X	Y	X-Mx	Y-My	(X-Mx)2	(X-Mx)(Y-My)
3	6	-1	-1	1	1
5	9	1	2	1	2
1	3	-3	-4	9	12
7	10	3	3	9	9
Mx=4	My=7			Sum=20	Sum=24

Если что M – это среднее арифмическое(вроде очевидно, но мало ли что очевидно…)



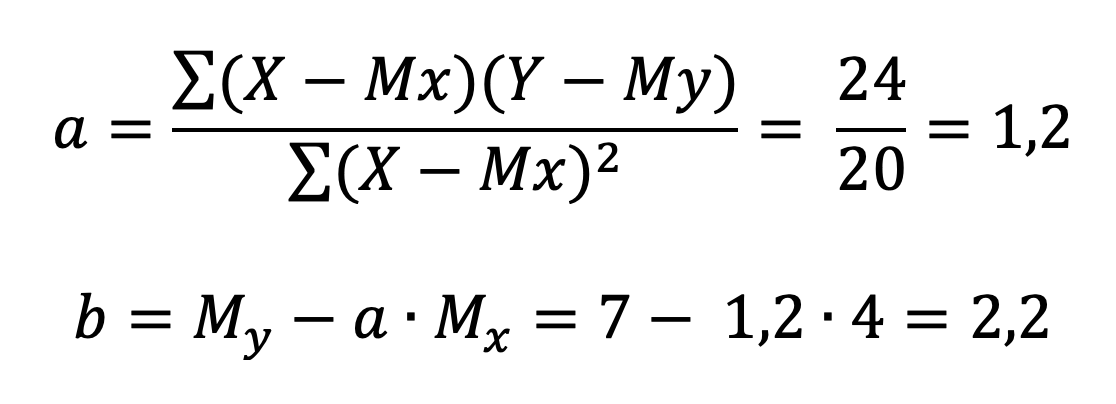
Собираем наш конструктор и получаем



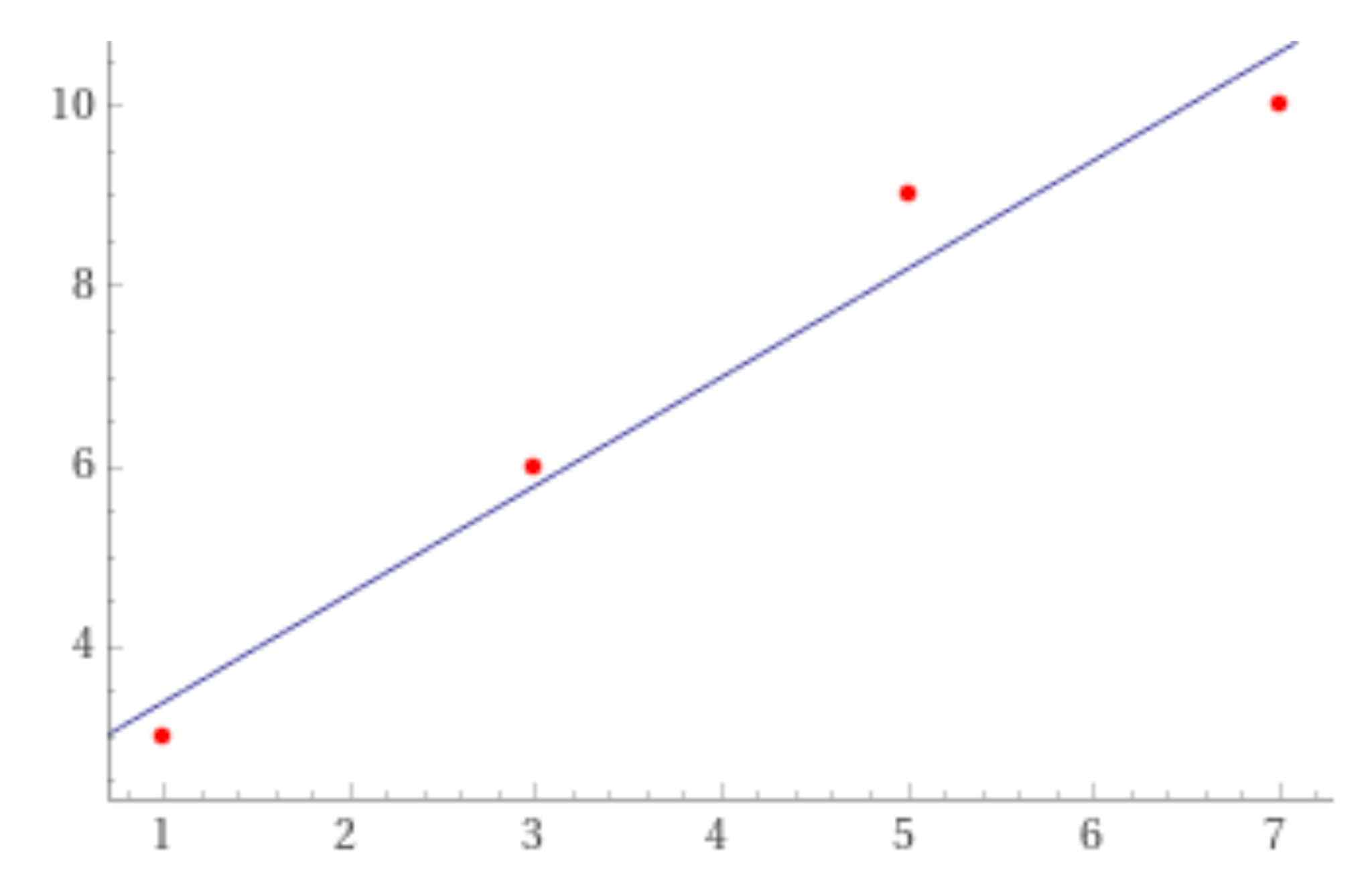
Для построения графика линейной регрессии нужно провести график прямой из получившегося уравнения, а потом проставить точки на графике из имеющихся данных

В нашем случае получается:




20. Оценка качества регрессии. Использование среднеквадратической ошибки. Для чего используется коэффициент детерминации R²? Приведите практический пример и найдите коэффициент детерминации для собственных данных. Сделайте вывод о разбросе данных
К оглавлению

Мы увидели, что при нахождении уравнения регрессии, мы подбираем такую функцию, для которой сумма квадратов ошибок будет наименьшей. Именно на этом показателе основывается одна из метрик для оценки качества построенного уравнения - среднеквадратичная ошибка (MSE - mean squared error). Для того чтобы ее вычислить, необходимо сумму квадратов ошибок разделить на количество наблюдений.

---

Из вопроса 20 возьмем данные и рассчитанное уравнение



— это значение y, которое мы считаем, подставляя x в уравнение.

Пример для первой строки

X	Y
3	6	5,8	-0,2	0,04
5	9	8,2	-0,8	0,64
1	3	3,4	0,4	0,16
7	10	10,6	0,6	0,36

Теперь считаем ср. арифм. последнего столбца



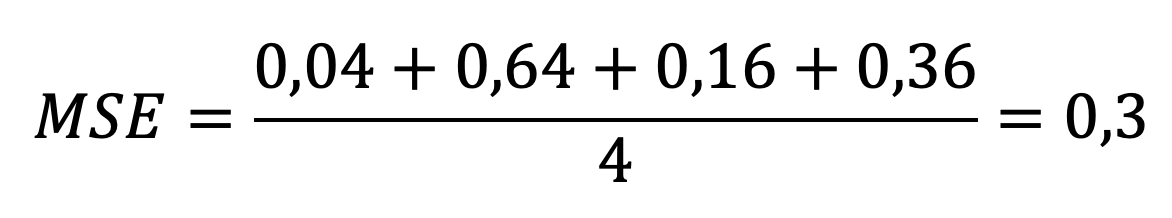
Вспомним, что мы возводили ошибки в квадрат для того, чтобы все показатели ошибок были положительными. Но избавиться от отрицательных чисел можно не только с помощью возведения в квадрат: также можно брать и модули. Метрика, которая вычисляется как сумма модулей ошибок, деленная на количество наблюдений, называется средняя абсолютная ошибка - MAE (mean absolute error).

X	Y
3	6	5,8	-0,2	0,2
5	9	8,2	-0,8	0,8
1	3	3,4	0,4	0,4
7	10	10,6	0,6	0,6

---

Теперь считаем ср. арифм. последнего столбца



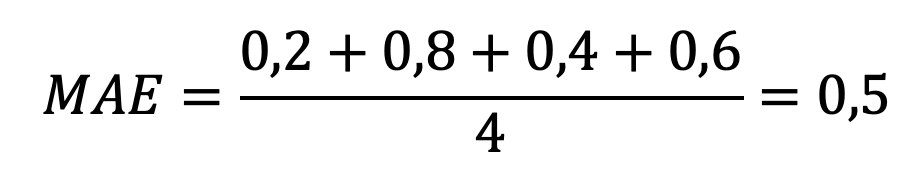
И есть еще одна метрика, по которой мы можем оценить качество нашей модели - коэффициент детерминации, R²

Коэффициент детерминации отражает, какой процент разброса данных мы можем объяснить нашей моделью.

Для того, чтобы рассчитать коэффициент детерминации, необходимо найти отклонения от среднего для целевой переменной и отклонения от среднего для предсказания целевой переменной. И после этого разделить первый результат в квадрате на второй результат в квадрате.

M_y=7

X	Y		Y-My		(Y-My)2
3	6	5,8	-1	-1,2	1	1,44
5	9	8,2	2	1,2	4	1,44
1	3	3,4	-4	-3,6	16	12,96
7	10	10,6	3	3,6	9	12,96
					Sum=30	Sum=28,36

Это означает, что мы можем объяснить с помощью нашего уравнения 94,5% данных (какие мы крутыеее)

21. Логистическая регрессия. Для решения каких задач применяется алгоритм? Напишите определение шанса. Выведите логистическую функцию, постройте её график. Приведите пример нахождения оценки вероятности для своего линейного уравнения.

---

К оглавлению

Логистическая регрессия — это метод машинного обучения, который используется для решения задач бинарной классификации, то есть разделения объектов на два класса (например, "да" или "нет", "истина" или "ложь", "заболевание" или "здоровье" и т.д.). Примеры задач, где используется логистическая регрессия, включают определение того, является ли электронное письмо спамом или не спамом, определение того, будет ли клиент покупать определенный продукт, или нет, и так далее.
Шанс (отношение вероятности успеха к вероятности неудачи) для события можно определить как отношение вероятности события к вероятности противоположного события. Например, если вероятность того, что команда выиграет матч, равна 0,8, то шансы на победу будут равны 0,8 / 0,2 = 4. То есть, шансы на победу в матче для команды равны 4 к 1.

​

Логистическая функция, также называемая сигмоидой, определяет вероятность отнесения объекта к одному из двух классов в зависимости от значения линейной комбинации его признаков (суём в функцию число и получаем вероятность от 0 до 1 (0 - объект не принадлежит классу, 1 - объект принадлежит классу)), чтобы ее вывести, вернемся к шансу. Запишем формулу шанса наступления события



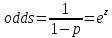
Чтобы получить вероятность p, мы решаем это уравнение относительно p:



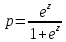
После простых алгебраических преобразований мы можем записать это выражение в виде логистической функции:



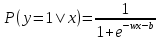
где w - вектор весов

x - вектор признаков

b - свободный член.
График этой функции выглядит как S-образная кривая, которая изменяется от 0 до 1:



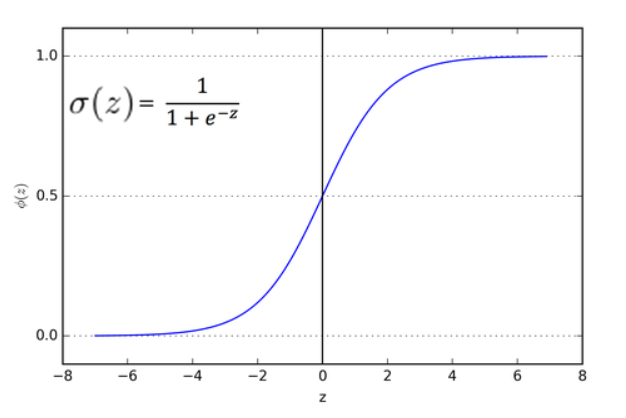
Для нахождения оценки вероятности для своего линейного уравнения необходимо подставить его в логистическую функцию и вычислить значение. Например, если линейное уравнение имеет вид y = 2x + 1, то соответствующее уравнение для логистической регрессии будет выглядеть следующим образом:



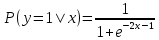
Подставляя значения признаков, можно вычислить вероятность отнесения объекта к классу 1.
22. Алгоритм Naïve Bayes. Для решения каких задач применяется алгоритм? Сформулируйте формулу теоремы Байеса. Объясните смысл составных частей. Почему алгоритм называется «наивным»? Приведите практический пример применения алгоритма Naïve Bayes для задачи фильтрации СПАМ-сообщений.

---