Файл: 1. Классификация признаков данных (Качественные и количественные, непрерывные и дискретные). Номинальные, порядковые, интервальные, дихотомические, относительные переменные.docx

Если в распоряжении аналитика оказалась нерепрезентативная выборка и при этом исходная совокупность для повторной выборки недоступна или повторное выборочное исследование невозможно (из-за высоких затрат или невозможности воспроизвести условия, при которых выборка была получена), то аналитик может произвести так называемый ремонт выборки — комплекс мер повышения репрезентативности.

Смещение выборки (sample bias) - это ошибка, возникающая в результате использования неслучайной или неправильно подобранной выборки для анализа генеральной совокупности. Такая выборка может быть не репрезентативной, то есть не отражать характеристики и свойства генеральной совокупности, и, следовательно, приводить к искаженным или неверным выводам при анализе данных.

Например, если проводить опрос только среди людей определенной возрастной группы, это может привести к смещению выборки, если результаты опроса не будут представлять характеристики и мнение всей популяции.

Чтобы избежать смещения выборки, важно проводить исследования на репрезентативных выборках, учитывать разнообразие групп и характеристик в генеральной совокупности, а также использовать различные методы и техники, такие как стратифицированная выборка, случайная выборка и др.

---

3. Частотные распределения. Разница между нормальным и равномерным распределением. Приведите пример визуализации графика распределения для своего набора данных.

К оглавлению

Частотное распределение — метод статистического описания данных (измеренных значений, характерных значений). Частотное распределение можно представить не только в виде таблицы, но и визуализировать его. Для этого есть два типа диаграмм: гистограмма и полигон.

Для построения гистограммы по оси абсцисс (оси х ) откладываются все возможные значения, а по оси ординат (оси у) — частоты. Если мы построим гистограмму для примера с оценками, то она будет выглядеть следующим образом:

Значение	Частота
2	5
3	10
4	6
5	4

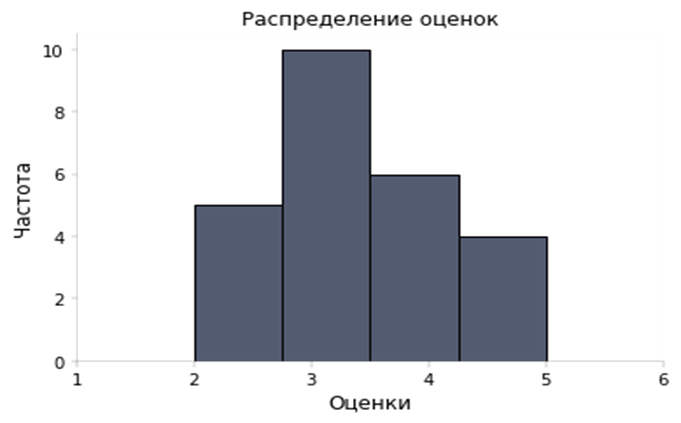
Ровно так же, как построена данная гистограмма, мы можем построить и гистограмму по сгруппированным частотам для примера с баллами ЕГЭ:



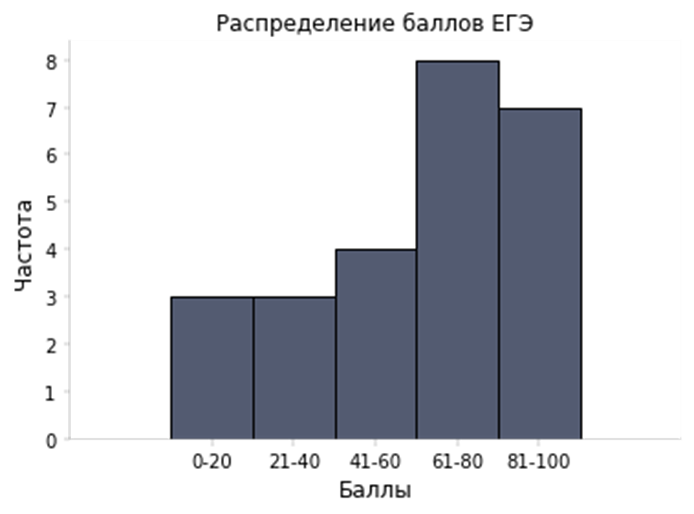
Однако важно помнить, что ее можно построить только для количественных данных.

Гистограмма — не единственный вариант визуализации частотного распределения. Также мы можем построить полигон распределения. Для этого нам необходимо отметить точки на области построения, которые соответствуют высоте столбца (как если бы мы строили гистограмму). После того как все точки отмечены, их соединяют, и получается полигон:



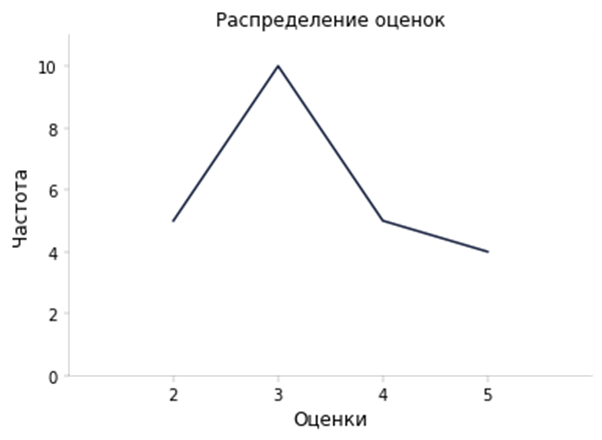
Таким образом, частотное распределение можно представлять как в формате таблицы, так и в графическом: гистограммы или полигона. Однако важно отметить, что полигон является скорее вспомогательным типом визуализации, который используется редко, обычно для визуального представления распределений наилучшим вариантом является гистограмма.

---

Гистограмма отлично подходит для визуализации количественных данных, но нам важно уметь в аналогичном виде представлять распределение частот для порядковых и номинальных данных. Аналогом гистограммы для качественных данных является столбчатая диаграмма. Для ее построения нужны ровно те же действия, что и для гистограммы, но визуально она немного отличается: между столбцами для разных категорий есть расстояние.

Предположим, что мы решили узнать, какие домашние животные есть у группы людей. Мы узнали, что собаки есть у пятерых людей, кошки — у десяти, четверо держат попугаев, и еще у двоих дома живут ящерицы:

Животное	Частота
Собака	5
Кошка	10
Попугай	4
Ящерица	2

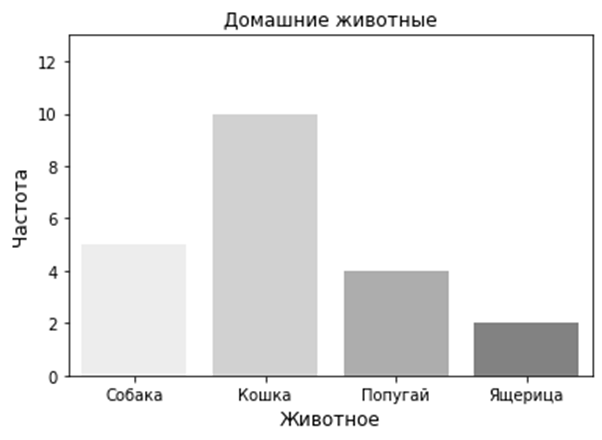
Теперь по данной таблице частот мы можем построить столбчатую диаграмму. Для каждого животного просто нарисуем столбец, высота которого будет соответствовать частоте.

Если мы визуализируем распределение порядкового признака, то категории обычно располагаются в упорядоченном виде: по возрастанию или убыванию. Для номинального признака значения никак нельзя упорядочить, поэтому столбцы могут располагаться в любом порядке, но чаще для простоты интерпретации их располагают от самого высокого до самого низкого.
Нормальное распределение является наиболее часто используемым в статистике распределением вероятностей.

Он имеет следующие свойства:

•Симметричный

•колоколообразный

Равномерное распределение — это такое распределение вероятностей, при котором каждое значение в интервале от a до b равновероятно.

Он имеет следующие свойства:

•Симметричный

•прямоугольной формы



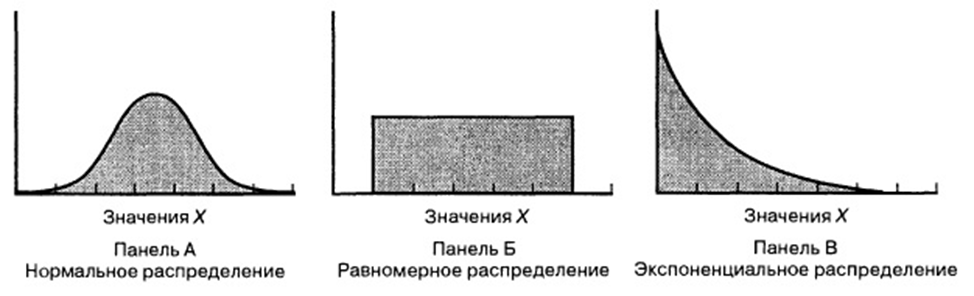
Нормальное распределение и равномерное распределение имеют следующее сходство :

---

•Оба распределения симметричны. То есть, если бы мы провели линию по центру распределения, левая и правая стороны распределения были бы идеально зеркальны друг другу:

Однако эти два дистрибутива имеют следующее различие :

•Распределения имеют разную форму.

•Нормальное распределение имеет колоколообразную форму, что означает, что значения вблизи центра распределения более вероятны, чем значения в хвостах распределения.

•Равномерное распределение имеет прямоугольную форму, что означает, что каждое значение в распределении встречается с одинаковой вероятностью.

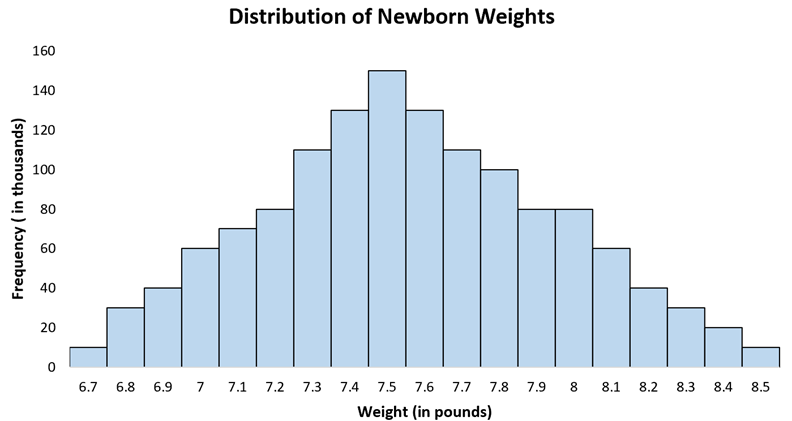
Нормальное распределение используется для моделирования явления, которое имеет тенденцию следовать форме «колоколообразной кривой». Например, хорошо задокументировано, что вес новорожденных при рождении обычно распределяется со средним значением около 7,5 фунтов.

Гистограмма массы тела при рождении новорожденных в США имеет колоколообразную форму, которая обычно имеет нормальное распределение:

Большинство младенцев, вероятно, будут весить около 7,5 фунтов, при этом немногие весят менее 7 фунтов, а немногие - более 8 фунтов.



И наоборот, равномерное распределение используется для моделирования сценариев, в которых каждый потенциальный результат равновероятен.

Классический пример — бросание игральной кости. Если вы бросаете игральную кость один раз, вероятность того, что она выпадет на число от 1 до 6, будет равномерно распределена, потому что все числа выпадут с одинаковой вероятностью.

Например, существует 6 возможных чисел, на которые может выпасть кубик, поэтому вероятность того, что выпадет 1, равна 1/6.

Точно так же вероятность того, что выпадет 2, равна 1/6.

Точно так же вероятность того, что вы выбросите 3, равна 1/6.

И так далее.

В равномерном вероятность попасти на любой участок равной меры (длины, площади итд) - одинакова, в нормальном - вероятность больше около центра, по мере удаления - быстро убывает.

---

4. Визуализация данных. Линейный график, столбчатые диаграммы, гистограммы, диаграммы рассеяния. Изобразить графически, описать суть графиков.

К оглавлению
Визуализация данных - это представление данных в виде, который обеспечивает наиболее эффективную работу человека по их изучению.

Линейный график

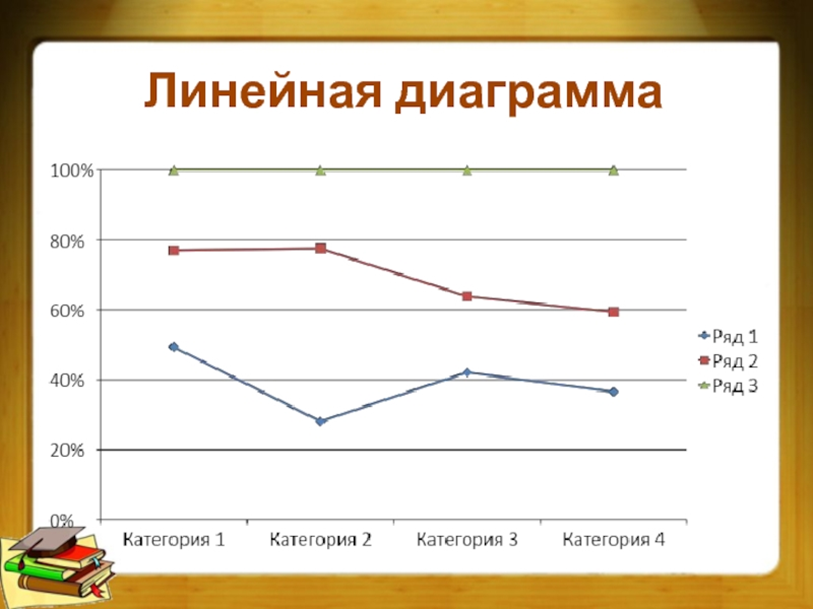
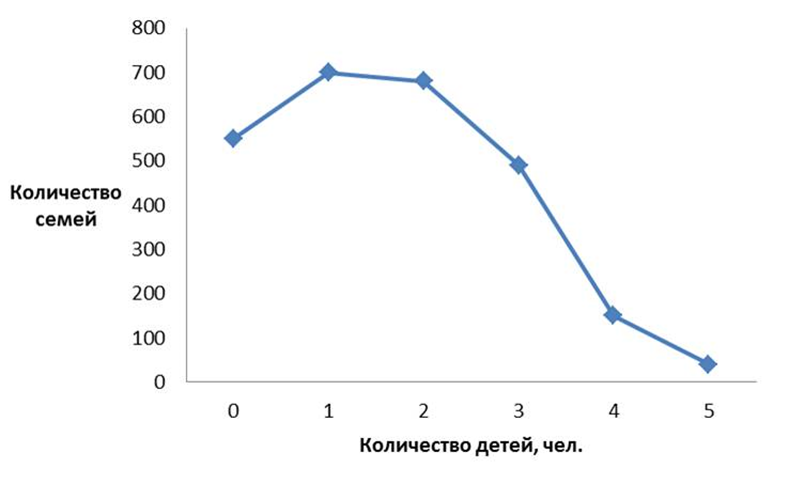
Линейная диаграмма или линейный график, также известный как кривая диаграмма, представляет собой тип диаграммы, которая отображает информацию в виде ряда точек данных, называемых "маркерами", соединенных отрезками прямой линии.

Линейный график (или линейная диаграмма) показывает динамику по одному либо нескольким показателям. Его удобно применять, когда нужно сравнить, как меняются с течением времени разные наборы данных.

Данные на таком графике отображаются в виде точек, которые соединены линиями. Также точки могут быть невидимыми, тогда график представляет собой ломаные линии.





Столбчатая диаграмма

Диаграмма, представленная прямоугольными зонами, высоты или длины которых пропорциональны величинам, которые они отображают. Прямоугольные зоны могут быть расположены вертикально или горизонтально. Столбчатая диаграмма отображает сравнение нескольких дискретных категорий.

Столбчатые диаграммы используются для отображения результатов сравнения одного показателя в разных условиях (например, результатов социологических опросов).

Столбчатые диаграммы необходимо представлять в виде отдельных столбиков одинаковой ширины, поскольку они представляют дискретные данные, и никогда не должны связываться линией.





Гистограмма

Способ представления табличных данных в графическом виде - в виде столбчатой диаграммы. Количественные соотношения некоторого

---