Файл: Методические рекомендации по выполнению курсового проекта по дисциплине Математические модели в экономике.doc
Добавлен: 25.10.2023
Просмотров: 139
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
r = 0,935.
Задание 2.3. Найти значение коэффициента корреляции для проверки статистической зависимости между годовым объемом работы по грузообороту (x) и фондоемкостью перевозок (y) по данным своего варианта.
Задание 2.4. Определить значимость найденного в задании 2.3 коэффициента корреляции. Сделать вывод о доверительности найденного значения, используя таблицу нижних границ значимости коэффициента корреляции с уровнем значимости 0,95. Вывод о значимости найденного значения линейного коэффициента корреляции в 95 случаях из 100 принимается при условии, что оно больше соответствующей нижней границы. В табл. П2 приложения приведены значения нижних границ коэффициента корреляции.
2.3 Выравнивание рядов распределений с проверкой гипотезы
нормальности по критерию Пирсона на базе эмпирического ряда
величин себестоимости железнодорожной перевозки
Задание 2.5. Требуется подтвердить гипотезу нормальности распределения эмпирического ряда величин себестоимости пропуска транзитных вагонов по участкам железных дорог и найти теоретическое нормальное распределение этих величин. Для этого необходимо установить величину расхождения между указанными распределениями, используя критерий Пирсона. Исходные данные для расчетов приведены в табл. 2.4 (интервалы распределения эмпирического ряда величин себестоимости пропуска транзитных вагонов по участкам железных дорог (варианты – первое значение шифра)), табл. 2.5 (распределение эмпирического ряда величин себестоимости пропуска транзитных вагонов по участкам железных дорог, тыс. руб./в-км (варианты – второе значение шифра)) и табл. 2.6 (необходимые формы).
Среднее значение ряда рассчитывается по формуле:
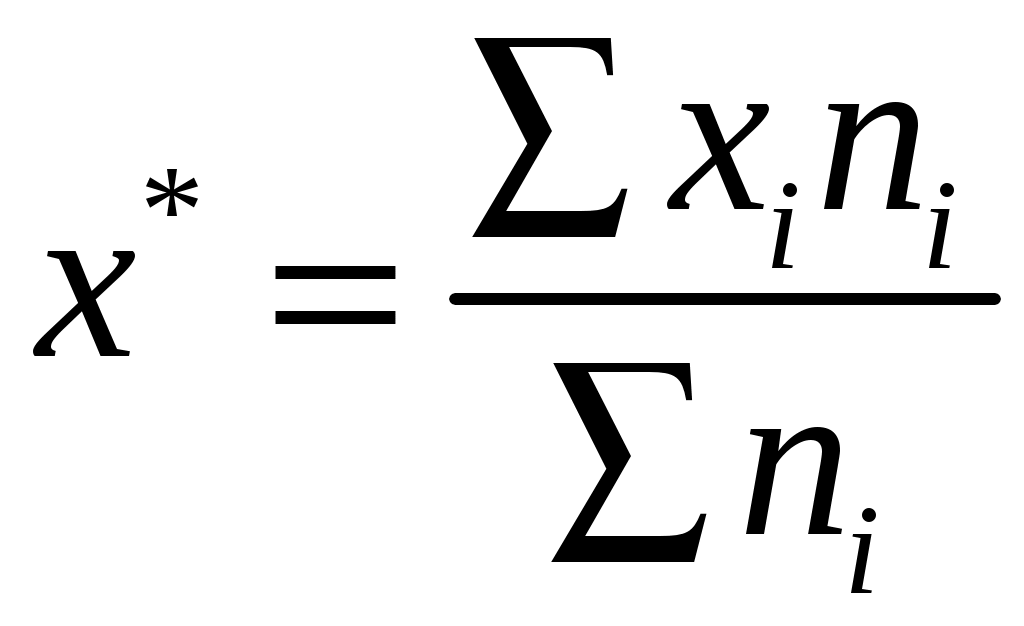 = 364/210 = 1,73.
= 364/210 = 1,73.
Таблица 2.4
Таблица 2.5
Таблица 2.6

Среднеквадратичное отклонение рассчитывается по формуле:
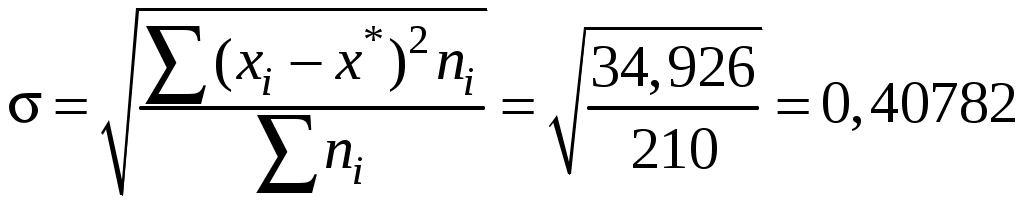 .
.
Нормированное отклонение рассчитывается по формуле:
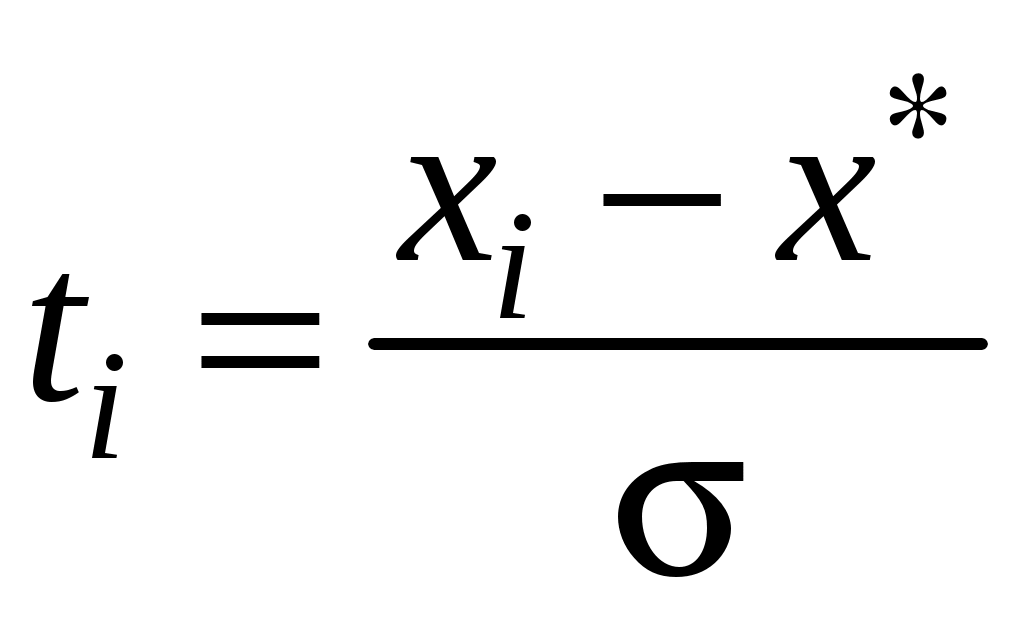 .
.
Теоретическое нормальное распределение нормируется через данный показатель путем умножения значения функции плотности вероятности φ(t)
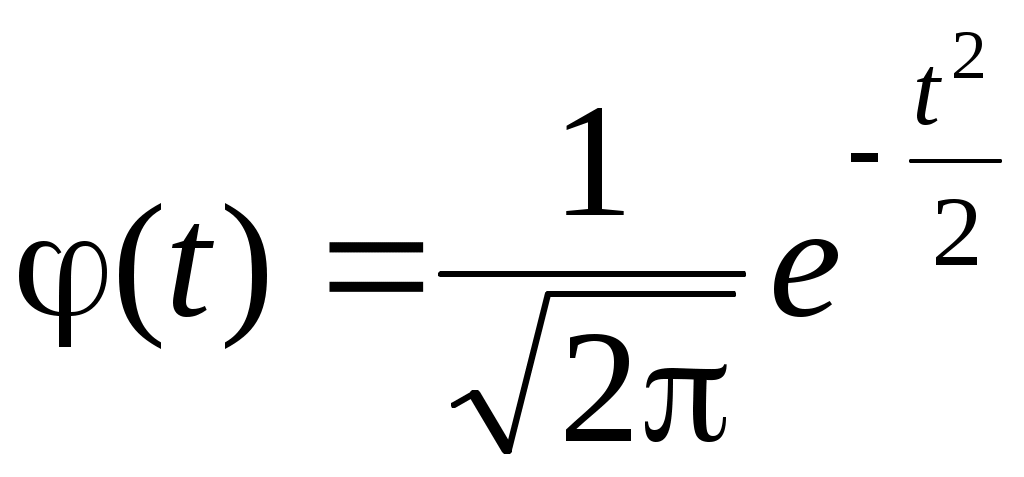
на значение величины эмпирического нормированного отклонения:
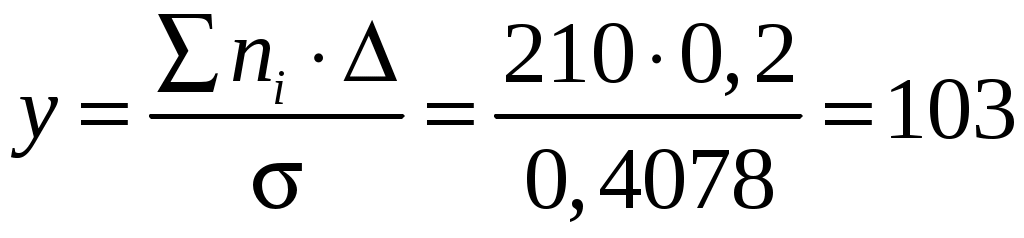 ;
; 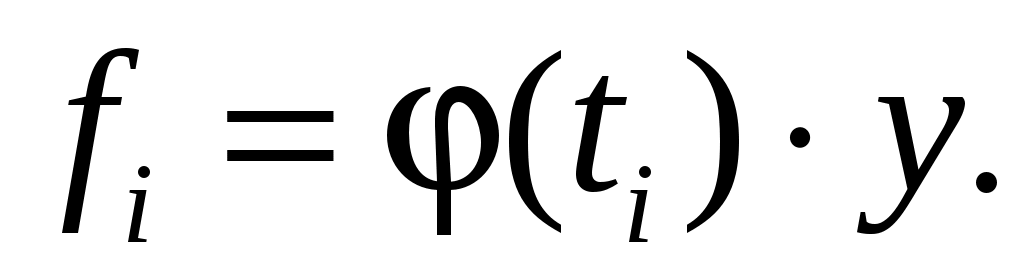
Данные по функции плотности вероятности φ(t) приведены в приложении, табл. П3. Сумма найденных теоретических частот ∑fi сравнивается с суммой частот эмпирического распределения ∑ni. Если эти суммы различаются незначительно, то предполагают, что расхождения фактического распределения с теоретической нормальной кривой распределения носят случайный характер, и гипотеза соответствия экспериментального распределения теоретическому принимается. В противном случае гипотеза соответствия отвергается. В практике статистических расчетов для оценки правомерности гипотезы соответствия фактического распределения нормальному принят критерий «-квадрат», иначе говоря, критерий Пирсона:
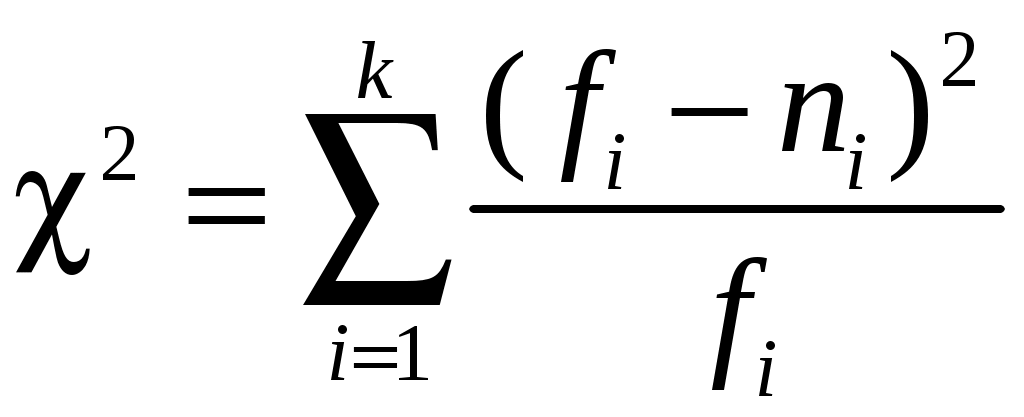 .
.
После определения величины критерия Пирсона рассчитывается число степеней свободы: r = k – 3, где k – число интервалов в фактическом распределении, длина каждого из которых Δ. В нашем примере: r = k – 3 = 11 – 3 = = 8. При заданном уровне значимости 5 %, предусматривающем 5%-ю ошибку, и количестве степеней свободы, равном у нас 8, определяется табличная величина критерия Пирсона χ2 = 15,5, приведенная в табл. 2.7. Если найденное значение в расчетах -квадрата меньше или равно табличному, гипотеза о соответствии эмпирического распределения теоретическому принимается
, если нет, то отвергается, как в нашем примере: χ2 = 24,94 > 15,5.
Таблица 2.7
2.4 Прогнозирование экономических показателей методом
простого экспоненциального сглаживания
Задание 2.3. Найти значение коэффициента корреляции для проверки статистической зависимости между годовым объемом работы по грузообороту (x) и фондоемкостью перевозок (y) по данным своего варианта.
Задание 2.4. Определить значимость найденного в задании 2.3 коэффициента корреляции. Сделать вывод о доверительности найденного значения, используя таблицу нижних границ значимости коэффициента корреляции с уровнем значимости 0,95. Вывод о значимости найденного значения линейного коэффициента корреляции в 95 случаях из 100 принимается при условии, что оно больше соответствующей нижней границы. В табл. П2 приложения приведены значения нижних границ коэффициента корреляции.
2.3 Выравнивание рядов распределений с проверкой гипотезы
нормальности по критерию Пирсона на базе эмпирического ряда
величин себестоимости железнодорожной перевозки
Задание 2.5. Требуется подтвердить гипотезу нормальности распределения эмпирического ряда величин себестоимости пропуска транзитных вагонов по участкам железных дорог и найти теоретическое нормальное распределение этих величин. Для этого необходимо установить величину расхождения между указанными распределениями, используя критерий Пирсона. Исходные данные для расчетов приведены в табл. 2.4 (интервалы распределения эмпирического ряда величин себестоимости пропуска транзитных вагонов по участкам железных дорог (варианты – первое значение шифра)), табл. 2.5 (распределение эмпирического ряда величин себестоимости пропуска транзитных вагонов по участкам железных дорог, тыс. руб./в-км (варианты – второе значение шифра)) и табл. 2.6 (необходимые формы).
Среднее значение ряда рассчитывается по формуле:
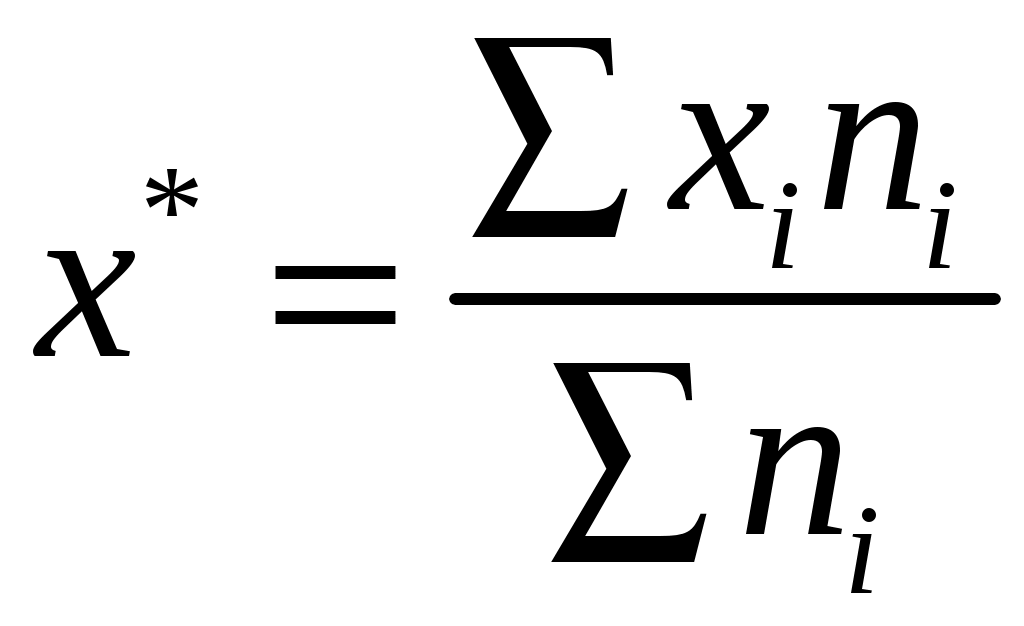 = 364/210 = 1,73.
= 364/210 = 1,73.Таблица 2.4
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | ||||||||||
| 0,56 | 0,76 | 0,58 | 0,78 | 0,6 | 0,8 | 0,62 | 0,82 | 0,64 | 0,84 | 0,66 | 0,86 | 0,68 | 0,88 | 0,7 | 0,9 | 0,72 | 0,92 | 0,74 | 0,94 |
| 0,76 | 0,96 | 0,78 | 0,98 | 0,8 | 1 | 0,82 | 1,02 | 0,84 | 1,04 | 0,86 | 1,06 | 0,88 | 1,08 | 0,9 | 1,1 | 0,92 | 1,12 | 0,94 | 1,14 |
| 0,96 | 1,16 | 0,98 | 1,18 | 1 | 1,2 | 1,02 | 1,22 | 1,04 | 1,24 | 1,06 | 1,26 | 1,08 | 1,28 | 1,1 | 1,3 | 1,12 | 1,32 | 1,14 | 1,34 |
| 1,16 | 1,36 | 1,18 | 1,38 | 1,2 | 1,4 | 1,22 | 1,42 | 1,24 | 1,44 | 1,26 | 1,46 | 1,28 | 1,48 | 1,3 | 1,5 | 1,32 | 1,52 | 1,34 | 1,54 |
| 1,36 | 1,56 | 1,38 | 1,58 | 1,4 | 1,6 | 1,42 | 1,62 | 1,44 | 1,64 | 1,46 | 1,66 | 1,48 | 1,68 | 1,5 | 1,7 | 1,52 | 1,72 | 1,54 | 1,74 |
| 1,56 | 1,76 | 1,58 | 1,78 | 1,6 | 1,8 | 1,62 | 1,82 | 1,64 | 1,84 | 1,66 | 1,86 | 1,68 | 1,88 | 1,7 | 1,9 | 1,72 | 1,92 | 1,74 | 1,94 |
| 1,76 | 1,96 | 1,78 | 1,98 | 1,8 | 2 | 1,82 | 2,02 | 1,84 | 2,04 | 1,86 | 2,06 | 1,88 | 2,08 | 1,9 | 2,1 | 1,92 | 2,12 | 1,94 | 2,14 |
| 1,96 | 2,16 | 1,98 | 2,18 | 2 | 2,2 | 2,02 | 2,22 | 2,04 | 2,24 | 2,06 | 2,26 | 2,08 | 2,28 | 2,1 | 2,3 | 2,12 | 2,32 | 2,14 | 2,34 |
| 2,16 | 2,36 | 2,18 | 2,38 | 2,2 | 2,4 | 2,22 | 2,42 | 2,24 | 2,44 | 2,26 | 2,46 | 2,28 | 2,48 | 2,3 | 2,5 | 2,32 | 2,52 | 2,34 | 2,54 |
| 2,36 | 2,56 | 2,38 | 2,58 | 2,4 | 2,6 | 2,42 | 2,62 | 2,44 | 2,64 | 2,46 | 2,66 | 2,48 | 2,68 | 2,5 | 2,7 | 2,52 | 2,72 | 2,54 | 2,74 |
| 2,56 | 2,76 | 2,58 | 2,78 | 2,6 | 2,8 | 2,62 | 2,82 | 2,64 | 2,84 | 2,66 | 2,86 | 2,68 | 2,88 | 2,7 | 2,9 | 2,72 | 2,92 | 2,74 | 2,94 |
1 2 3 4 5 6 7 8 9 10
Таблица 2.5
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 2 | 3 | 4 | 2 | 4 | 3 | 2 | 4 | 3 | 2 |
| 7 | 8 | 6 | 7 | 6 | 8 | 7 | 6 | 8 | 5 |
| 14 | 12 | 10 | 14 | 10 | 12 | 14 | 10 | 12 | 12 |
| 20 | 21 | 18 | 20 | 18 | 21 | 20 | 18 | 21 | 18 |
| 30 | 29 | 30 | 30 | 30 | 29 | 30 | 30 | 29 | 24 |
| 42 | 40 | 40 | 40 | 40 | 40 | 40 | 42 | 42 | 38 |
| 50 | 48 | 36 | 48 | 48 | 36 | 36 | 50 | 50 | 29 |
| 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 21 |
| 22 | 22 | 24 | 22 | 22 | 24 | 24 | 22 | 22 | 17 |
| 12 | 10 | 10 | 10 | 10 | 10 | 10 | 12 | 12 | 9 |
| 6 | 4 | 2 | 4 | 4 | 2 | 2 | 6 | 6 | 2 |
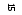
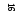
Таблица 2.6
| X1 | X2 | ni | Xi | Xini | Xi – X* | (Xi– X*)2 | (Xi – X*)2 ni | ti | φ(ti) | fi | fi – ni | (fi – ni)2 | (fi – ni)2/fi |
| 0,6 | 0,8 | 2 | 0,7 | 1,4 | –1,0333 | 1,0678 | 2,1356 | –2,5 | 0,0163 | 1,68 | –0,321 | 0,1032 | 0,0615 |
| 0,8 | 1 | 5 | 0,9 | 4,5 | –0,8333 | 0,6944 | 3,4722 | –2 | 0,0498 | 5,13 | 0,1287 | 0,0166 | 0,0032 |
| 1 | 1,2 | 10 | 1,1 | 11 | –0,6333 | 0,4011 | 4,0111 | –1,6 | 0,12 | 12,4 | 2,3584 | 5,5620 | 0,4501 |
| 1,2 | 1,4 | 20 | 1,3 | 26 | –0,4333 | 0,1878 | 3,7556 | –1,1 | 0,2275 | 23,4 | 3,429 | 11,7610 | 0,5020 |
| 1,4 | 1,6 | 40 | 1,5 | 60 | –0,2333 | 0,0544 | 2,1778 | –0,6 | 0,3391 | 34,9 | –5,077 | 25,778 | 0,7382 |
| 1,6 | 1,8 | 60 | 1,7 | 102 | –0,0333 | 0,0011 | 0,0667 | –0,1 | 0,3977 | 41 | –19,04 | 362,607 | 8,8532 |
| 1,8 | 2 | 23 | 1,9 | 43,7 | 0,1667 | 0,0278 | 0,6389 | 0,41 | 0,3683 | 37,9 | 14,92 | 222,902 | 5,8767 |
| 2 | 2,2 | 20 | 2,1 | 42 | 0,3667 | 0,1344 | 2,6889 | 0,9 | 0,2685 | 27,7 | 7,65 | 58,551 | 2,1174 |
| 2,2 | 2,4 | 14 | 2,3 | 32,2 | 0,5667 | 0,3211 | 4,4956 | 1,39 | 0,1539 | 15,8 | 1,84 | 3,4211 | 0,2158 |
| 2,4 | 2,6 | 10 | 2,5 | 25 | 0,7667 | 0,5878 | 5,8778 | 1,88 | 0,0694 | 7,15 | –2,857 | 8,1381 | 1,1386 |
| 2,6 | 2,8 | 6 | 2,7 | 16,2 | 0,9667 | 0,9344 | 5,6067 | 2,37 | 0,0241 | 2,48 | –3,51 | 12,376 | 4,9866 |
| | 210 | | 364 | | | 34,926 | y = 103 | | 209,5 | | | χ2 = 24,94 | |

Среднеквадратичное отклонение рассчитывается по формуле:
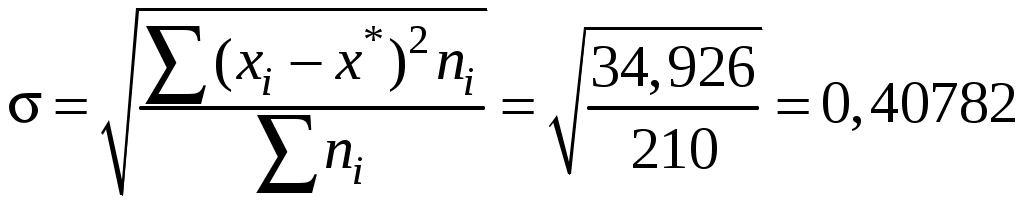 .
.Нормированное отклонение рассчитывается по формуле:
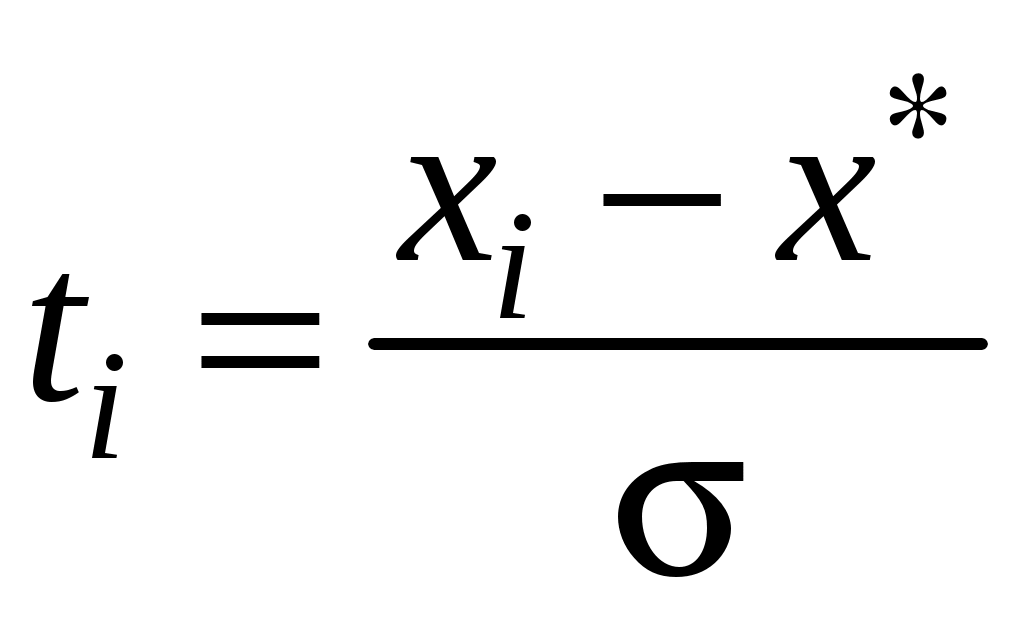 .
.Теоретическое нормальное распределение нормируется через данный показатель путем умножения значения функции плотности вероятности φ(t)
на значение величины эмпирического нормированного отклонения:
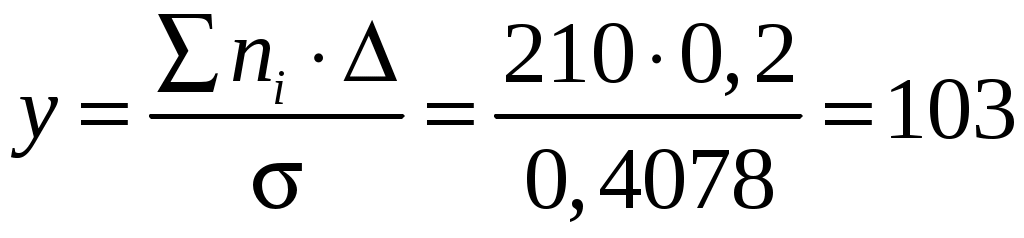 ;
; Данные по функции плотности вероятности φ(t) приведены в приложении, табл. П3. Сумма найденных теоретических частот ∑fi сравнивается с суммой частот эмпирического распределения ∑ni. Если эти суммы различаются незначительно, то предполагают, что расхождения фактического распределения с теоретической нормальной кривой распределения носят случайный характер, и гипотеза соответствия экспериментального распределения теоретическому принимается. В противном случае гипотеза соответствия отвергается. В практике статистических расчетов для оценки правомерности гипотезы соответствия фактического распределения нормальному принят критерий «-квадрат», иначе говоря, критерий Пирсона:
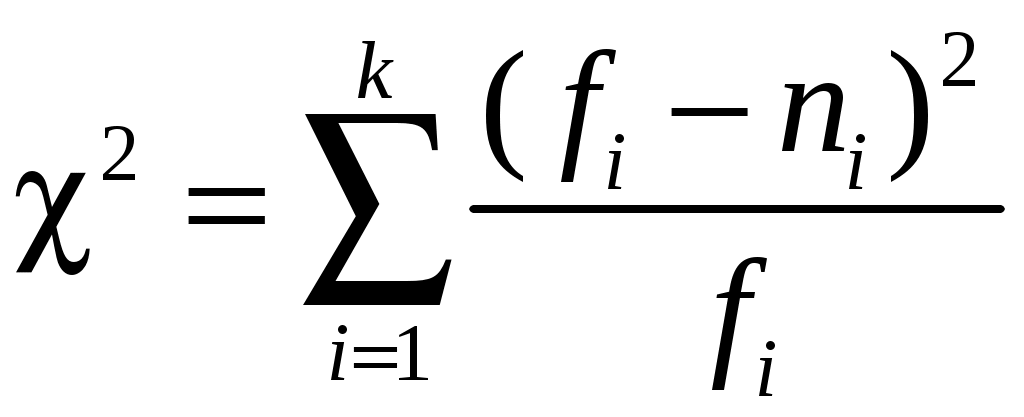 .
.После определения величины критерия Пирсона рассчитывается число степеней свободы: r = k – 3, где k – число интервалов в фактическом распределении, длина каждого из которых Δ. В нашем примере: r = k – 3 = 11 – 3 = = 8. При заданном уровне значимости 5 %, предусматривающем 5%-ю ошибку, и количестве степеней свободы, равном у нас 8, определяется табличная величина критерия Пирсона χ2 = 15,5, приведенная в табл. 2.7. Если найденное значение в расчетах -квадрата меньше или равно табличному, гипотеза о соответствии эмпирического распределения теоретическому принимается
, если нет, то отвергается, как в нашем примере: χ2 = 24,94 > 15,5.
Таблица 2.7
| Число степеней свободы | 5%-е критические значения | Число степеней свободы | 5%-е критические значения | Число степеней свободы | 5%-е критические значения |
| 1 | 3,8 | 11 | 19,7 | 21 | 32,7 |
| 2 | 6,0 | 12 | 21,0 | 22 | 33,9 |
| 3 | 7,8 | 13 | 22,4 | 23 | 35,2 |
| 4 | 9,5 | 14 | 23,7 | 24 | 36,4 |
| 5 | 11,1 | 15 | 25,0 | 25 | 37,7 |
| 6 | 12,6 | 16 | 26,3 | 26 | 38,9 |
| 7 | 14,1 | 17 | 27,6 | 27 | 40,1 |
| 8 | 15,5 | 18 | 28,9 | 28 | 41,3 |
| 9 | 16,9 | 19 | 30,1 | 29 | 42,6 |
| 10 | 18,3 | 20 | 31,4 | 30 | 43,8 |
2.4 Прогнозирование экономических показателей методом
простого экспоненциального сглаживания