. Если условие оптимальности не выполняется, переходим к шагу 5, иначе получен оптимальный и допустимый план.

Шаг5.Выбор ключевого столбца. Из показателей индексной строки выбирается значение с наибольшим отклонением от условия оптимальности. Соответствующая переменная на следующей итерации входит в базис задачи.

Шаг6.Выбор ключевой строки. Находится минимальное отношение показателей столбцов x_i и a_ij при условии, что  0.

Шаг7. Выполняются симплекс-преобразования:
, ,
где – значение элемента в новом базисе;

– значение элемента ключевой строки в новом базисе;

– значение элемента в текущем базисе;

– значение элемента ключевой строки в текущем базисе;

– значение элемента ключевого столбца в текущем базисе;

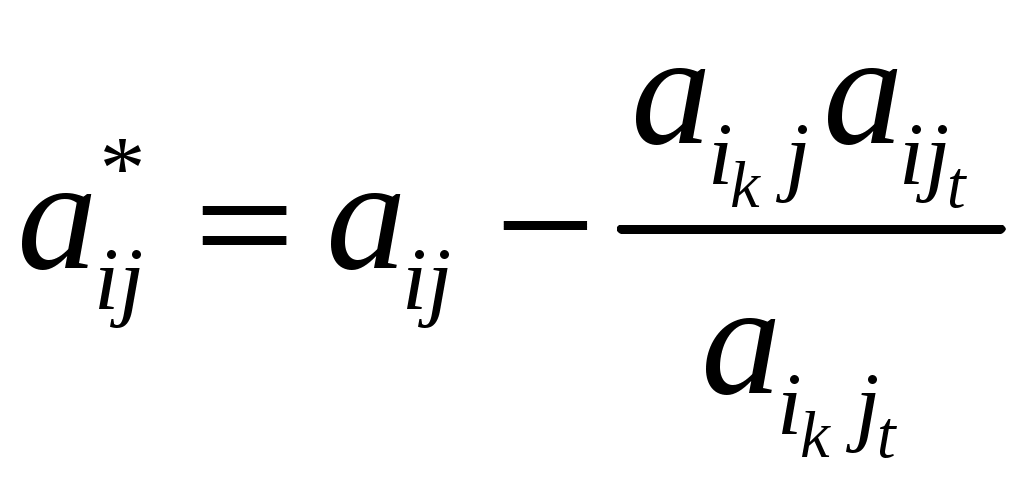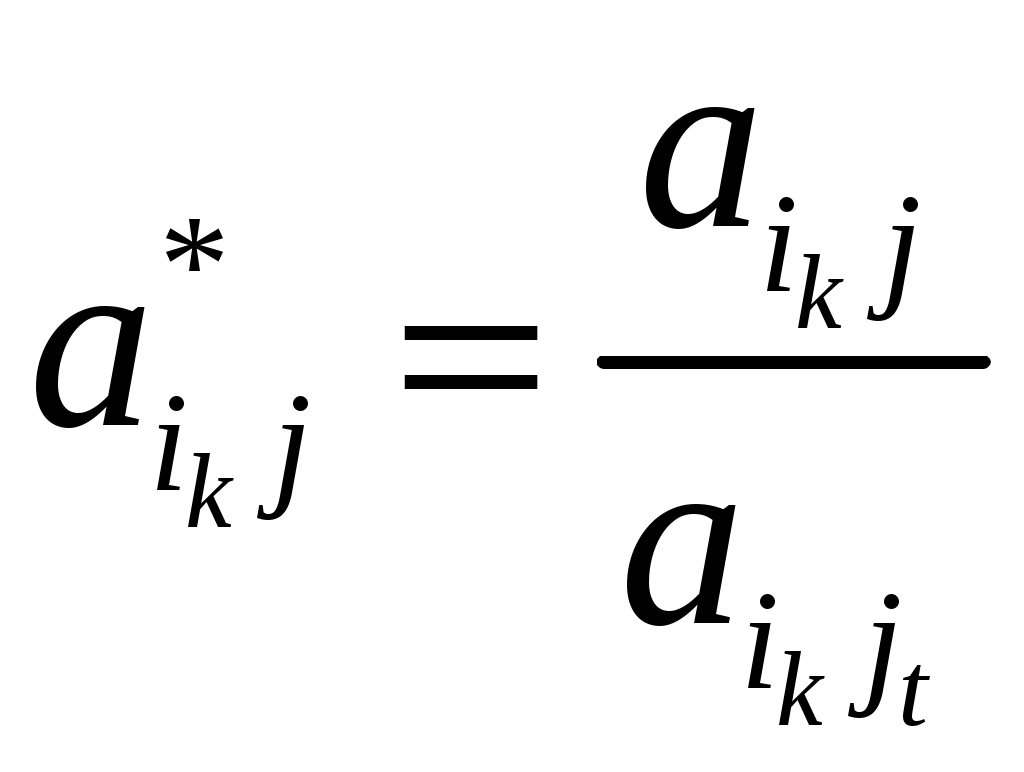– значение ключевого элемента в текущем базисе.
Пример 3.1. Вначале заполняется таблица 3.4. Сюда занесем значения коэффициентов функции цели, наименования неизвестных, массив значений коэффициентов «затраты – выпуск», формирования столбцов c_i, p_i, x_i, составляющих базис плана, полученный при использовании канонической формы с переменными x₅, x₆, x₇.
Таблица

---

3.4

ci	pi	xi	3	4	3	1	0	0	0
			x1	x2	x3	x4	x5	x6	x7
0	x5	12	2	4	0	8	1	0	0
0	x6	8	7	2	2	6	0	1	0
0	x7	48	5	8	4	3	0	0	1
zj – cj		0	–3	–4	–3	–1	0	0	0

Шаги 1, 2, 3, 4.

Шаг 5. Выбор ключевого столбца – (x₂). Переменная x₂ входит в базис.

Шаг 6. Выбор ключевой строки: min {12/4; 8/2; 48/8} = 12/4. Переменная x₅ исключается из базиса.

Шаг 7. Симплексные преобразования. Переходим к табл. 3.5.
Таблица3.5

ci	pi	xi	3	4	3	1	0	0	0
			x1	x2	x3	x4	x5	x6	x7
4	x2	3	1/2	1	0	2	1/4	0	0
0	x6	2	6	0	2	2	–1/2	1	0
0	x7	24	1	0	4	–13	–2	0	1
zj – cj		12	–1	0	–3	7	1	0	0

---

Шаг 4.

Шаг 5. Выбор ключевого столбца – (x₃). Переменная x₃ входит в базис.

Шаг 6. Выбор ключевой строки: min {2/2; 24/4} = 2/2. Переменная x₆ исключается из базиса.

Шаг 7. Симплексные преобразования. Переходим к табл. 3.6.


Таблица3.6

ci	pi	xi	3	4	3	1	0	0	0
			x1	x2	x3	x4	x5	x6	x7
4	x2	3	1/2	1	0	2	1/4	0	0
3	x3	1	3	0	1	1	–1/4	1/2	0
0	x7	20	–11	0	0	–17	–1	–2	1
zj – cj		15	8	0	0	10	1/4	3/2	0

Шаг 4. Проверка условия оптимальности. План оптимален, поскольку все показатели индексной строки неотрицательны.
3.2 Изучение модифицированного симплекс-метода
Имеется возможность выпуска четырех видов продукции (N1, N2, N3, N4) на пяти типах машин (A, B, C, D, E).

1. Сформировать математическое описание задачи.

2. Построить каноническую форму и получить допустимое решение.

3. Определить оптимальный план.

4. Выполнить анализ оптимального производственного плана, включая состав и объем выпуска продукции, получаемую при этом прибыль, эффективность и состояние использованных ресурсов.

5. Проанализировать возможность изменения оптимального плана, привлекая для этого двойственные оценки и другие показатели индексной строки.

---

Исходные данные приведены в табл. 3.1–3.3. Каждый студент получает свой вариант расчета – двухзначный шифр.

В табл. 3.1 приведены данные по коэффициентам «затраты – выпуск», общие для всех вариантов. В табл. 3.2 приведены данные по коэффициентам целевой функции по вариантам с первой цифрой шифра. В табл. 3.3 приведены данные по ресурсам по вариантам со второй цифрой шифра.

---

Пример 3.2. Вначале заполняется таблица 3.7. Сюда занесем значения коэффициентов функции цели, наименования неизвестных, массив значений коэффициентов «затраты – выпуск».
Таблица 3.7

N3	N2	N1	3	4	3	1	0	0	0
			x1	x2	x3	x4	x5	x6	x7
1/4	1	0	2	4	0	8	1	0	0
3/2	0	0	7	2	2	6	0	1	0
0	0	0	5	8	4	3	0	0	1
			–3	–4	–3	–1	0	0	0
			–1	0	–3	7	1	0	0
			8	0	0	10	1/4	3/2	0

Заполнение таблицы 3.8 начнем с формирования столбцов c_i, p_i, x_i, составляющих базис плана

---

Смотрите также файлы

• Транспортная логистика (часть 11) Кокурин Д. И.pdf

• Практическая работа Задание.docx

• Кафедра доклад по дисциплине Тема Синектика Студент(ка) Козлова Ангелина Юрьевна Л112211 группы.docx

• Функция Назначение.docx

• Баллов 1 из Отметить вопрос.pdf