ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.04.2021
Просмотров: 419
Скачиваний: 1
11
тод
1
–
наименее
точный
,
то
для
обеспечения
условия
1
2
3
P
P
P
P
=
=
=
(
)
1
2
3
S
S
S
=
=
,
необходимо
,
чтобы
интервалы
x
D
были
связаны
соотноше
-
нием
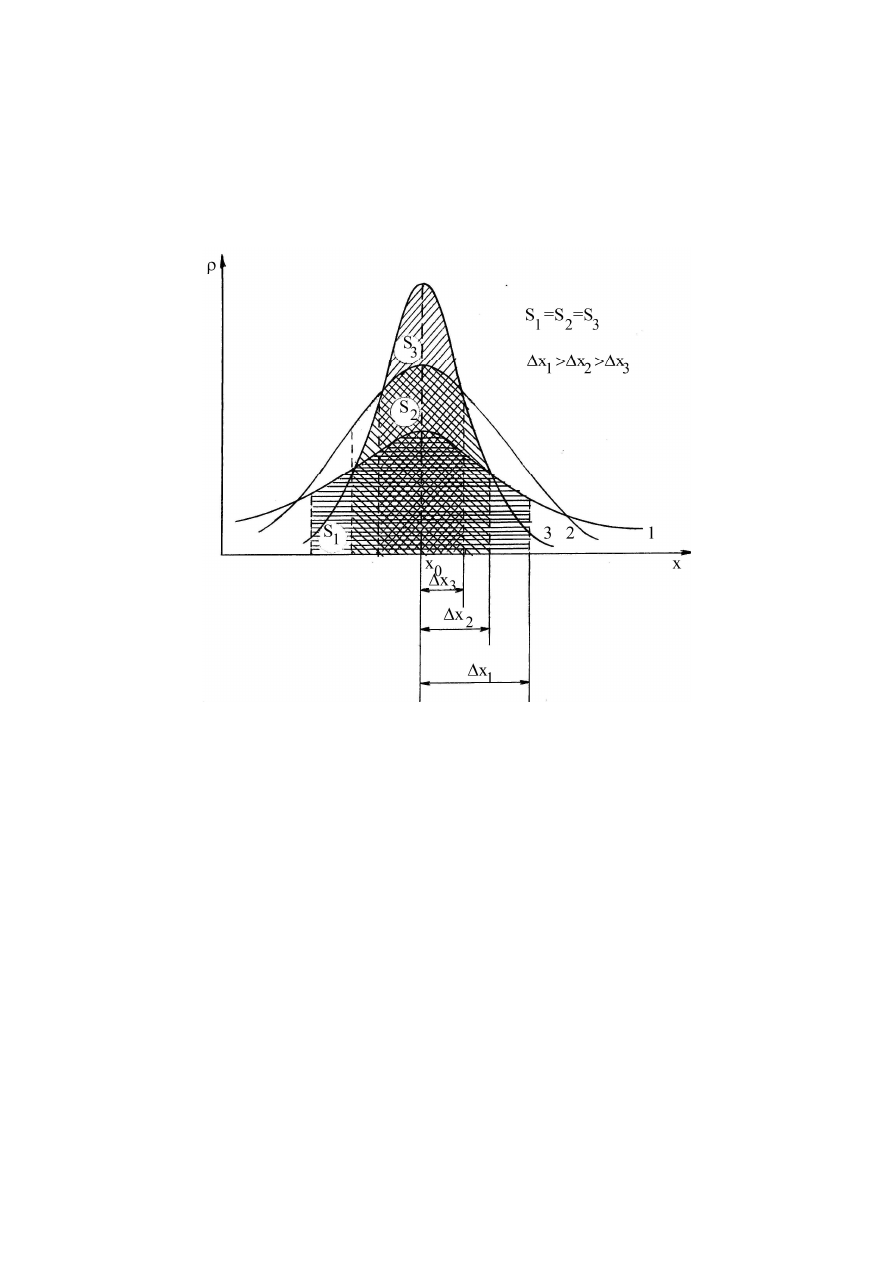
1
2
3
x
x
x
D > D > D
(
рис
. 3.4).
Таким
образом
,
величина
интервала
x
D
связана
с
точностью
метода
:
повышение
точности
метода
приводит
к
уменьшению
интервала
x
D
.
Рис
. 3.4
При
измерении
произвольной
физической
величины
х
,
истинное
зна
-
чение
которой
равно
А
ист
,
можно
выполнить
большое
(
в
пределе
–
беско
-
нечное
)
количество
измерений
.
Ряд
полученных
результатов
1
2
3
,
,
, ... ,...
n
x
x
x
x
называют
генеральной
(
общей
)
совокупностью
значений
.
Разность
между
результатом
i-
го
измерения
( )
i
x
и
истинным
значением
(
А
ист
)
называется
истинной
абсолютной
погрешностью
i-
го
измерения
:
1
01
2
02
3
03
0
,
,
,
..........................
,
..........................
ист
ист
ист
n
ист
n
x
A
x
x
A
x
x
A
x
x
A
x
-
= D
ì
ï -
= D
ï
ï -
= D
ï
í
ï
ï -
= D
ï
ïî
(3.7)
12
Рис
. 3.5
Суммирование
левых
и
правых
частей
уравнений
системы
(3.7)
даёт
:
0
1
1
lim
lim
n
n
i
ист
i
n
n
i
i
x
n
А
x
®¥
®¥
=
=
æ
ö
- ×
=
D
ç
÷
è
ø
å
å
.
Окончательно
1
1
1
lim
lim
lim
n
n
n
i
i
i
i
i
i
ист
n
n
n
x
x
x
А
x
n
n
n
=
=
=
®¥
®¥
®¥
D
=
-
»
=
å
å
å
. (3.8)
Следовательно
,
при
большом
количестве
измерений
x
приближённо
при
-
нимается
равным
А
ист
(
однако
среднее
значение
не
равно
истинному
).
Математическая
теория
обработки
результатов
позволяет
рассчитать
интервал
(
) (
)
,...
сл
сл
x
x
x
x
é
ù
- D
+ D
ë
û
,
в
котором
с
заданной
вероятностью
Р
находится
истинное
значение
измеряемой
величины
.
Величина
сл
x
D
назы
-
вается
случайной
составляющей
погрешности
.
Для
определения
сл
x
D
необ
-
ходимо
по
результатам
n
наблюдений
1
2
3
,
,
, ...
n
x
x
x
x
вычислить
x
и
приближённые
абсолютные
погрешности
измерений
i
x
D
:
1
1
2
2
3
3
,
,
,
..........................
.
n
n
x
x
x
x
x
x
x
x
x
x
x
x
- = D
ì
ï - = D
ïï
- = D
í
ï
ï
- = D
ïî
(3.9)
Для
характеристики
степени
рассеяния
результатов
измерений
вели
-
чины
i
x
около
истинного
значения
А
ист
используется
понятие
дисперсии
(
от
латинского
dispersio
–
рассеяние
).
Дисперсия
обозначается
символом
( )
D x
и
рассчитывается
по
формуле
:
2
2
1
(
)
( )
lim
n
i
i
x
n
x
x
D x
n
s
=
®¥
-
=
=
å
. (3.10)
Здесь
x
s
–
средняя
квадратичная
ошибка
генеральной
совокупности
,
число
измерений
при
этом
бесконечно
.
Оценка
(3.10)
подобрана
так
,
что
при
проведении
многочисленных
наблюдений
погрешность
в
2/3
случаев
оказывается
меньше
x
s
,
а
в
1/3
случаев
больше
,
чем
x
s
.
Исследуя
случайные
погрешности
,
К
.
Гаусс
установил
закон
распределения
случайных
погрешностей
,
или
просто
закон
распределения
Гаусса
.
Согласно
этому
закону
,
при
числе
13
наблюдений
,
стремящемся
к
бесконечности
,
частота
появления
случайных
по
-
грешностей
у
определяется
формулой
:
( )
2
2
2
1
,
2
x
y
e
s
s
p
D
-
×
=
×
×
×
(3.11)
где
s
–
средняя
квадратичная
погрешность
,
x
D
–
ошибка
измерения
.
Гра
-
фик
закона
нормального
распределения
ошибок
(3.11)
представлен
на
рис
. 3.5
для
различных
значений
s
(
3
2
1
s
s
s
>
>
).
Закон
распределения
Гаусса
отражает
следующие
положения
теории
случайных
погрешностей
:
1)
случайные
погрешности
обоих
знаков
встречаются
одинаково
часто
;
2)
меньшие
случайные
погрешности
встречаются
чаще
,
чем
большие
;
3)
очень
большие
погрешности
маловероятны
.
Закон
распределения
Гаусса
является
типичным
статистическим
за
-
коном
.
Он
подергался
многократным
экспериментальным
проверкам
,
ко
-
торые
показали
,
что
этот
закон
выполняется
тем
точнее
,
чем
больше
про
-
ведено
наблюдений
.
Закон
Гаусса
имеет
основополагающее
значение
для
разработки
критериев
оценок
точности
измерений
,
а
также
при
обработке
результатов
физических
измерений
.
В
реальных
условиях
число
выполняемых
измерений
физической
ве
-
личины
,
как
правило
,
невелико
.
Поэтому
вместо
генеральной
совокупно
-
сти
значений
физической
величины
,
для
которой
n
® ¥
,
ограничиваются
конечным
числом
n
измерений
.
В
этом
случае
дисперсия
генеральной
со
-
вокупности
заменяется
выборочной
дисперсией
:
2
2
1
(
)
( )
1
n
i
i
x
x
x
D x
S
n
=
-
=
=
-
å
. (3.12)
Среднее
квадратичное
отклонение
отдельного
измерения
:
2
1
(
)
1
n
i
i
x
x
x
S
n
=
-
=
-
å
(3.13)
называют
также
средней
квадратичной
погрешностью
измерения
.
Она
яв
-
ляется
мерой
разброса
результатов
измерений
и
характеризует
точность
применяемого
метода
измерений
.
Среднее
квадратичное
отклонение
результата
серии
измерений
:
(
)
2
1
(
)
1
n
i
x
i
x
x
x
S
S
n
n n
=
-
=
=
×
-
å
(3.14)
позволяет
определить
погрешность
измерения
физической
величины
в
ре
-
зультате
всех
n
выполненных
измерений
.
Появление
конкретных
случайных
ошибок
не
является
абсолютно
предсказуемым
событием
.
Об
этом
можно
судить
лишь
с
определённой
14
степенью
вероятности
.
Вероятность
того
,
что
истинное
значение
величины
х
заключено
в
интервале
от
x
x
- D
до
x
x
+ D
,
равна
:
(
)
(
)
P x
x
x
x
x
a
- D < <
+ D
=
é
ù
ë
û
. (3.15)
Здесь
x
x
+ D
называется
верхней
доверительной
границей
,
x
x
- D
–
ниж
-
ней
доверительной
границей
,
интервал
(
) (
)
,
x
x
x
x
- D
+ D
é
ù
ë
û
–
доверитель
-
ным
интервалом
.
Вероятность
a
называется
доверительной
вероятно
-
стью
и
выражается
в
процентах
или
в
долях
единицы
.
Между
средней
квадратичной
погрешностью
x
S
и
доверительной
вероятностью
существу
-
ет
следующая
зависимость
:
x
S
соответствует
a
=
0,68, 2
x
S
соответствует
a
=
0,95, 3
x
S
соответствует
a
=
0,997.
При
окончательной
оценке
резуль
-
тата
измерений
наряду
со
средней
квадратичной
ошибкой
x
S
указывают
величину
доверительной
вероятности
a
.
Чем
выше
доверительная
вероят
-
ность
,
тем
шире
доверительный
интервал
и
тем
большее
число
измерений
укладывается
в
этот
интервал
.
Поэтому
доверительную
вероятность
назы
-
вают
коэффициентом
надёжности
.
При
переходе
к
большим
значениям
a
и
сохранении
прежней
величины
доверительного
интервала
необходимо
уменьшить
среднюю
квадратичную
погрешность
,
то
есть
повысить
точ
-
ность
измерений
.
Точность
измерений
можно
повысить
путём
увеличения
числа
измерений
или
использованием
более
совершенных
приборов
.
Поскольку
при
малом
количестве
измерений
использование
распре
-
деления
Гаусса
становится
неправомерным
,
для
оценки
величины
довери
-
тельного
интервала
вводят
поправочный
коэффициент
Стьюдента
,
n
t
a
.
Случайную
погрешность
измерений
при
малом
числе
наблюдений
n
с
учё
-
том
коэффициента
Стьюдента
рассчитывают
по
формуле
:
2
1
,
,
(
)
(
1)
n
i
i
сл
n
x
n
x
x
x
t
S
t
n n
a
a
=
-
D
=
×
=
×
× -
å
. (3.16)
Коэффициент
Стьюдента
является
функцией
доверительной
вероятности
a
и
числа
измерений
n
(
приложение
,
табл
. 1).
Увеличение
числа
измере
-
ний
или
уменьшение
доверительной
вероятности
приводят
к
уменьшению
коэффициента
Стьюдента
.
При
исследованиях
в
учебной
лаборатории
принято
использовать
значения
коэффициента
,
n
t
a
,
равные
0,90
или
0,95.
4.
Случайная
погрешность
прямых
неравноточных
измерений
Полученные
выше
соотношения
применимы
в
случае
,
когда
одина
-
ково
доверяют
результату
каждого
отдельного
измерения
.
Однако
не
все
-
гда
удаётся
обеспечить
полную
воспроизводимость
условий
повторных
измерений
.
Нередко
сопоставление
результатов
нескольких
серий
наблю
-
дений
показывают
,
что
результаты
одной
серии
(
обозначим
её
А
)
менее
15
однородны
,
чем
в
другой
серии
(
Б
).
Результаты
серии
А
заслуживают
меньшего
доверия
,
но
их
не
следует
отбрасывать
.
Их
можно
учесть
,
уменьшив
их
роль
(
вес
)
в
совокупности
всех
результатов
измерений
.
Существуют
и
другие
причины
,
вызывающие
необходимость
умень
-
шить
роль
,
то
есть
«
вес
»
результатов
тех
или
иных
измерений
.
Например
,
из
-
мерения
могут
быть
выполнены
различными
приборами
,
которые
дают
нерав
-
ноценные
по
точности
результаты
,
или
измерения
могут
проводиться
различ
-
ными
операторами
,
имеющими
различную
квалификацию
и
опыт
.
Чтобы
выполнить
основное
требование
теории
погрешностей
:
обес
-
печить
единство
условий
измерений
в
отношении
всех
влияющих
факто
-
ров
,
необходимо
оценить
степень
доверия
,
то
есть
определить
«
вес
»
всех
результатов
,
подлежащих
обработке
.
Понятие
«
вес
»
отражает
степень
доверия
к
результату
измерения
:
чем
больше
доверие
к
результату
,
тем
больше
«
вес
»,
то
есть
тем
больше
выражающее
его
число
.
В
этом
случае
значение
измеряемой
величины
,
наиболее
близкое
к
её
истинному
значению
,
определяется
по
формуле
:
1
1
2
2
3
3
0
1
2
3
...
,
...
n
n
n
x p
x p
x p
x p
x
p
p
p
p
×
+ ×
+ ×
+ + ×
=
+
+
+ +
(4.1)
где
1
2
3
,
,
,...
n
x x
x
x
–
средние
значения
для
отдельных
групп
измерений
,
1
2
3
,
,
,...
n
p
p
p
p
–
их
«
вес
».
Значение
0
x
называется
средним
взвешенным
.
В
основу
вычисления
«
весов
»
взяты
средние
квадратичные
отклоне
-
ния
.
Веса
отдельных
измерений
считают
обратно
пропорциональными
квадратам
средних
квадратичных
отклонений
( )
2
x
S
,
то
есть
дисперсиям
:
1
2
3
2
2
2
2
1
2
3
1
1
1
1
:
:
:...:
:
:
:...:
m
m
p p p
p
S
S
S
S
=
, (4.2)
где
дисперсию
-
й
j
серии
измерений
определяют
по
формуле
(3.13):
2
1
(
)
1
n
i
i
xj
x
x
S
n
=
-
=
-
å
.
Предположим
,
например
,
что
тремя
наблюдателями
проведены
три
группы
измерений
.
В
результате
определены
средние
значения
,
а
по
фор
-
муле
(3.13)
определены
дисперсии
каждой
серии
:
1
1
2
1
3
1
1)
395,45;
0,05;
2)
395,15;
0,20;
3)
395,60;
0,10.
x
x
x
x
S
x
S
x
S
=
= ±
=
= ±
=
= ±
Определим
отношение
весов
:
(
) (
) (
)
1
2
3
2
2
2
1
1
1
1
1
1
:
:
:
:
:
:
0,025 0,04 0,01
0,05
0,20
0,10
400 : 25 :100 16 :1: 4.
p p p
=
=
=
=
=